Навигация
Методы экстракции статических параметров модели из результатов измерения характеристик и параметров
2.3 Методы экстракции статических параметров модели из результатов измерения характеристик и параметров
Ток насыщения IS в модели Э-М экстраполируется отрезком прямой тока зависимости lnIC от VBE в прямой области и lnIE от VBC в обратной области, как показано на рисунке 10. График зависимости рисунка 10 показывает смысл параметров IS и bF.
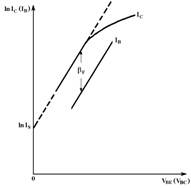
Рисунок 10 –График зависимости lnIC (lnIB)от напряжения VBE (VBC)
Напряжение Эрли VA может быть получено непосредственно из зависимости IC от VCE. Наклон этих характеристик в нормальной активной области g0 получается из уравнений (4) и (9), путём ослабления незначительный второго члена, и тогда дифференцируя относительно VBC (VBE принята постоянной), получим
 (38)
(38)
Геометрический смысл соотношения (38) показывает, что VA получается из отрезка прямой экстраполирующей наклон относительно оси VCE (как показано на кривой рисунка 5). Например, наклон (50 кОм)-1 при IC(0) = 1 мА дает, из уравнения (38), VA = 50 В.
Для определения параметра F необходимо построить график зависимости lnIC и lnIB как функции VBE, как показано на рисунке 11. Так как вертикальная ось логарифмическая, bF получается непосредственно из графика как расстояние между кривыми IC и IB.
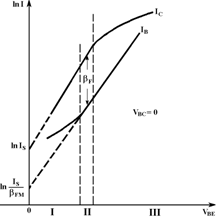
Рисунок 11 – График зависимости lnIC и lnIB от VBE при VBC = 0 [1]
График зависимости lnIB от qVBE/kT при VBC = 0, приведенный на рисунке 12, иллюстрирует два компонента тока IB: идеальная компонента с наклоном 1 и неидеальная с наклоном равным 1/nEL. Экстраполяция этих прямолинейных участков на ось у дает значения C2IS(0) и IS(0)/bFM(0).
Подобный график lnIB как функции от VBC для инверсного режима работы дает значения для параметров модели C4 и nCL. Типичное значение для C2 (и C4) составляет 103, а типовое значение для nEL (и nCL) - 2.
Из характеристики lnIC от VBE в двух экстремумах – высокого и низкого уровня инжекции – можно экспериментально определить параметр IKF.
Асимптота низкого тока дается следующим уравнением (для qe»qc»0):
![]() (39)
(39)
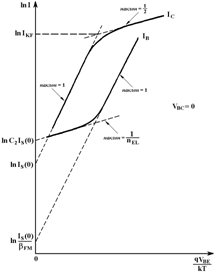
Рисунок 12 – График зависимости lnIC и lnIB от qVBE/kT при VBC = 0
Асимптота больших токов дается следующим соотношением
 (40)
(40)
Пересечение двух асимптот определяет ток излома IKF и соответствующее ему напряжение излома VKF.
Из соотношения (40) следует, что при высоком уровне инжекции
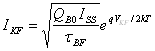 ,(41)
,(41)
в то время как из формулы (39) следует, что при низком уровне инжекции
![]() (42)
(42)
Из решений уравнений (41) и (42) получается
![]() (43)
(43)
Аналогично можно получить IKR, если построить график lnIE от VBC.
Дополнительный параметр модели Г-П может быть получен из поведения асимптоты в результате увеличения тока короткого замыкания IL (см. рисунок 6). Усиление по току постоянно при значении FМ для IC > IL; уменьшается с наклоном 1-nEL при IC < IL; и уменьшается с наклоном минус единица для токов IC > IKF. IL дается приближенным соотношением:
![]() (44)
(44)
3. Динамическая модель БТ в PSpice
3.1 Уравнения, описывающие электрические характеристики БТ в динамическом режиме
Рассмотрим эффекты накопления заряда в устройстве на примере модели Э-М. Накопление заряда в БТ моделируется включением трех типов конденсаторов: двух нелинейных конденсаторов, учитывающих барьерные емкости p-n-переходов, двух нелинейных конденсаторов, учитывающих диффузионные емкости переходов, и постоянного конденсатора перехода подложки [1].
Заряд, связанный с подвижными носителями в БТ, моделируется диффузионными емкостями. Этот заряд разделен на две составляющие: один связан с опорным источником коллекторного тока ICC, и другой с опорным источником тока эмиттера IEC. Каждый компонент отображается конденсатором.
Чтобы вычислить диффузионную емкость, связанную с ICC, необходимо рассмотреть общее число подвижных зарядов, связанных с этим током. Поэтому примем, что переход Б-Э прямо смещен и VBC=0.
Для упрощенного одномерного случая постоянно легированной базы, незначительной рекомбинации в базе, и низкого уровня инжекции в БТ (см. рисунок 13), сумма подвижных зарядов QDE, связанная с ICC, может быть записана как сумма отдельных неосновных зарядов:
![]() ,(45)
,(45)
где QE – заряд неосновных носителей, запасенный в эмиттерной области, QJE – заряд неосновных носителей в обедненной области перехода Э-Б, связанный с ICC (обычно принимают равным нулю), QBF – заряд неосновных носителей, накопленный в нейтральной области базы, QJC- заряд неосновных подвижных носителей в обедненной области перехода К-Б, связанный с ICC.
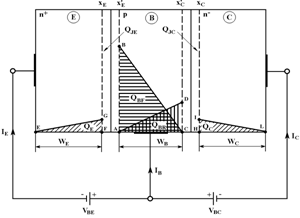
Рисунок 13 – Поперечный разрез n+-p-n- -транзистора, показывающий размещение компонент заряда [1]
Чтобы определить диффузионную емкость, необходимо рассмотреть только одну составляющую. Из уравнения (45) полный заряд подвижных носителей, связанный с ICC может также быть выражен как [1]
![]() ,(46)
,(46)
где tE – время задержки эмиттера; tEB - время пролета через ООЗ перехода Э-Б; tBF - время пролета базы; tCB - время пролета ООЗ перехода Б-К; и tF - общее прямое время пролета (принятое здесь постоянным), которое представляет среднее время для неосновных носителей, необходимое для того чтобы диффундировать через нейтральную область базы из эмиттера к коллектору. tЕB стремится к нулю.
Подобный анализ общего заряда подвижных носителей, связанного с IEC приводит к
![]() (47)
(47)
где QC – заряд неосновных подвижных носителей, накопленный в нейтральной области коллектора; QJC – заряд неосновных носителей в ООЗ перехода К-Б, связанный с IEC; QBR – заряд неосновных носителей, накопленный в нейтральной области базы; QJE - заряд неосновных носителей в ООЗ Э-Б, связанный с IEC. Если заряд QJC принять равным 0, тогда из уравнения (47) следует
![]() ,(48)
,(48)
где tC – время задержки коллектора, tBR - обратное время пролета Б, и tR - полное обратное время пролета (принят постоянным). tСB стремится к нулю.
Два заряда QDE и QDC моделируются двумя нелинейными конденсаторами
![]() (49)
(49)
![]()
как показано на рисунке 14.
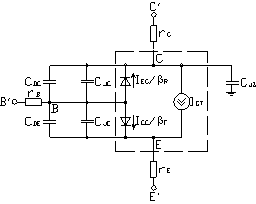
Рисунок 14 – Модель Эберса-Молла для большого сигнала
С ростом приращений на переходах неподвижные заряды QJE и QJC, накопленные в обедненных областях БТ, могут быть смоделированы двумя конденсаторами – называемыми барьерными емкостями. Эти емкости, обозначенные CJE для перехода Б-Э и CJC для коллекторного перехода, включены в модель, как это показано на рисунке 14. Каждая емкость перехода - нелинейная функция от напряжения на выводах перехода, с которым соединена.
В [1] показано, что обе эти зависимости имеют следующий вид:
![]() (50)
(50)
где CJ(0) – барьерная емкость при нулевом смещении, V – приложенное напряжение, f - контактная разность потенциалов перехода, m – показатель плавности перехода.
Для эмиттерного перехода и коллекторного переходов коэффициенты плавности равны по умолчанию mE = mC = 0,33.
Чтобы получить неподвижные заряды QJE и QJC, необходимо проинтегрировать барьерные емкости по их напряжению, то есть
 (51)
(51)

На рисунке 15 показаны три кривые зависимости барьерной емкости как функции напряжения [1].
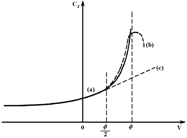
кривая (а) соответствует выражению (50)
кривая (b) показывает конечное изменение барьерной емкости
кривая (с) описывается соотношением (52)
Рисунок 15 – График изменения барьерной емкости с напряжением
Кривая (с) рисунка 15 представляет прямолинейное приближение, сделанное в соответствии с обычными компьютерными программами для V> f/2. Уравнение для этой прямой линии, полученной для соответствующего наклона в f/2, определяется как
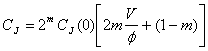 для V ³ f/2(52)
для V ³ f/2(52)
В этом приближении удается избежать бесконечной емкости. Но оно не столь точно как кривая Чавла-Гуммеля (b), однако, приемлемо потому, что под прямым смещением диффузионные емкости, доминируют и неотъемлемо включают эффект заряда подвижных носителей в обедненных областях [1].
В Spice используется прямолинейная аппроксимация для CJ подобная линии (с) рисунка 15. Уравнение (52) заменено следующим общим соотношением:
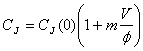 для V ³ 0(53)
для V ³ 0(53)
Помимо CJE и CJC, при проектировании интегральных схем должна быть принята во внимание еще одна емкость: емкость подложки CJS.
Хотя фактически это барьерная емкость в области с изменяющимся потенциалом эпитаксиальный слой – подложка, здесь она смоделирована как конденсатор с постоянным номиналом.
Это представление адекватно для большинства случаев, так как переход ЭС – подложка смещен в обратном направлении в целях изоляции.
Установив основные соотношения эффектов накопления заряда, покажем, как реализована модель Э-М для большого сигнала в Spice. Компоненты накопленных зарядов QBE = QDE + QJE и QBC = QDC + QJC моделируются конденсаторами CBE и CBC, включенными в эквивалентную схему модели так, как показано на рисунке 16.
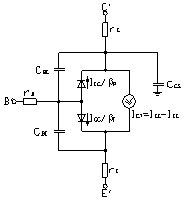
Рисунок 16 – Модель большого сигнала Эберса-Молла в Spice2
Компоненты заряда накопления представлены в PSpice следующими зависимыми от напряжения уравнениями емкости [1]:
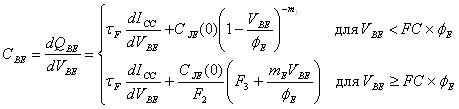 ,(54)
,(54)
 ,(55)
,(55)
 ,(56)
,(56)
где для эмиттерного перехода
 ,(57)
,(57)
для коллекторного перехода
 ,(58)
,(58)
где FC – коэффициент нелинейности барьерных емкостей прямосмещенных переходов, принимающий значения от 0 до 1. Коэффициенты плавности переходов хотя и включены в соотношения (54) – (58), фактически не учитываются в модели Э-М
В PSpice схема модели большого сигнала Г-П идентична схеме, приведенной на рисунке 16. Зависимые от напряжения емкости, определены соотношениями (54) - (58), причем здесь учитываются коэффициенты плавности mE, mC и mS (обычно, они изменяются между 0,33 и 0,5), а IEC и ICC рассматриваются как функции ISS и qB. Кроме того, модель большого сигнала Г-П, учитывает три дополнительных эффекта: распределенная емкость перехода Б-К, модуляция времени переноса заряда tF, и распределенные явления в области базы (стадия избытка).
Похожие работы
... САПРа затраты машинного времени на определение нелинейных функций, описывающих различные полупроводниковые приборы составляют значительную часть общих затрат времени. 1. Проблема математического моделирования биполярных транзисторов Под моделированием понимается описание электрических свойств полупроводникового устройства или группы таких устройств, связанных между собой, с помощью ...
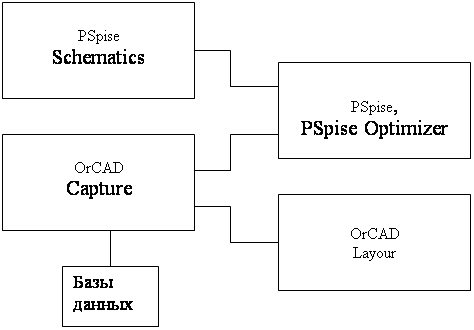
... того пользователь имеет возможность задать любые атрибуты по формату <имя атрибута>=<значение>Допускается рекурсия атрибутов. Этапы создания графической схем в системе автоматизированнного проектирования OrCAD Графический редактор Schematics пакета Design Center 6.2 на платформе Windows позволяет создавать чертежи принципиальных схем и передавать управление программам PSpice, ...
... кафедру для утверждения. После утверждения куратор проекта от кафедры проставляет оценку студенту. ЛИТЕРАТУРА Основная литература 1. Павлов В.Н., Ногин В.Н. Схемотехника аналоговых электронных устройств. М.: Радио и связь, 1997. 2. Ногин В.Н. Аналоговые электронные устройства. М.: Радио и связь, 1992. 304 с. 3. Остапенко Г.С. Усилительные устройства. М.: Радио и связь, 1989. 400 с. ...
... 2 – управляющее напряжение 2; 3 – выходной сигнал. Рисунок 3.12 – Диаграммы работы буфера управляющего напряжения. Промоделируем динамику работы всей схемы электрической принципиальной (приложение В). Реальный анализ схемы в составе импульсного источника питания в программе проектирования электронных схем не возможен ввиду использования с схеме импульсного трансформатора, модель которого в ...

0 комментариев