Модель БТ в статическом режиме работы
Снижение коэффициента усиления по току, наблюдаемое при больших токах;
Параметры, описывающие статическую модель БТ
Методы экстракции статических параметров модели из результатов измерения характеристик и параметров
Параметры модели БТ в динамическом режиме
Методы экстракции динамических параметров модели БТ из результатов измерения динамических характеристик и параметров
Навигация
Методы экстракции динамических параметров модели БТ из результатов измерения динамических характеристик и параметров
Определение параметров модели биполярного транзистора в программе OrCAD 9.2
47493
знака
1
таблица
33
изображения
3.3 Методы экстракции динамических параметров модели БТ из результатов измерения динамических характеристик и параметров
Характер изменения tF от IC показан на рисунке 18. Изменение tF при больших токах К обычно определяется эмпирическим уравнением, полученным из произведения полосы усиления fT и тока IC, при различных напряжениях К-Э VCE.
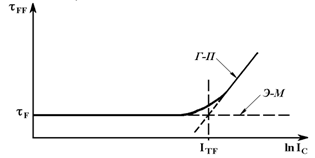
Рисунок 18 – График зависимость tF от lnIC
В области средних токов, fT находиться по его пиковому значению и почти постоянно; при этом время переноса заряда - время, необходимое н.з. для того, чтобы пересечь область базы и ООЗ коллекторного перехода. Диффузионная емкость перехода Э-Б увеличивается с током, уменьшая рост дифференциальной проводимости, имеющий результатом определенный предел для fT. Таким образом, идеальный максимум tF определяется из выражения [1]:
(61)
На больших токах, fT и к тому же tF становятся функцией IC и VCE и перестают быть постоянными (см. рисунок 18). Физические эффекты типа эффекта Кирка увеличивают время переноса и уменьшают fT. Эти эффекты смоделированы следующей эмпирической функцией [1]:
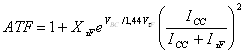(62)
tF умножают на ATF в уравнениях заряда. Постоянная 1,44 просто дает интерпретацию VtF как значение VBC, где экспонента равняется 1/2. XtF управляет полным спадом из-за fT ; VtF преобладает над изменением по fT относительно VCE; ItF доминирует над изменением по fT относительно тока.
Как видно из рисунка 18, ItF может быть получен путем экстраполяции прямой до пересечения с осью lnIC.
Можно показать [1], что
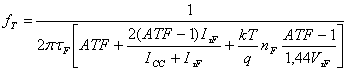(63)
В области слабых токов или высоких VCE (АТF = 1), выражение (63) сокращается до
(64)
При больших IC, таких, что ICC/(ICC + ItF) » 1 и средних VCE, формула (63) сократиться до
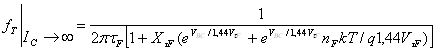(65)
Таким образом, асимптота сильных токов для данных VBC определена параметрами XtF и VtF. Аналогично, асимптотическая зависимость выражения (63) в экстремумах от VBC будет
, для IC®¥, VBC®0(66)
когда ATF » 1+XtF , при IC ® ¥, VBC ® 0(67)
Таким образом, максимально возможный спад в fT управляется параметром XtF. В PSpice, этот эффект выражен следующим выражением для заряда и эквивалентной емкости:
, (68)
,
где tFF - модулированное время переноса заряда через базу, данное выражением:
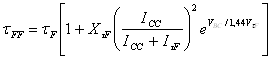,(69)
и tF - идеальное время переноса заряда в активном режиме. tF экстраполируется на ось y зависимости tFF от lnIC.
4. Зависимость параметров модели БТ от температуры и площади
Температурные зависимости параметров элементов эквивалентной схемы БТ устанавливается с помощью следующих выражений [1].
Здесь могут устанавливаться несколько температурных уравнений для РSpice параметров модели БТ, которые можно выбрать, установив параметры TLEV и TLEVC в опции .MODEL. В последующем, мы будем рассматривать только уравнения, выбранные с TLEV.
Температурная зависимость ширины ЗЗ Еg (ЕG) следует из выражения
Температурная зависимость bF (BF) определяются уравнением
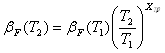
Температурная зависимость IS (IS) моделируется формулой
IBЕ (IBE) и IBC (IBC) определены
Температурная зависимость ISSUB (ISS) определена как
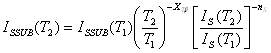
Зависимости параметров IKF (IKF), IKR (IKR) и IrB (IRB) от температуры представлены следующим образом:
где ТIKF1, ТIKR1, TIRB1 и TIKF2, TIKR2, TIRB2 температурные коэффициенты первого и второго порядка для соответствующих параметров, соответственно.
Следующие параметры определены для случая, когда соответствующие температурные коэффициенты определяются независимо от значения TLEV
Наконец, сопротивления, как функция температуры независимо от значения TLEV, определены следующим образом []:
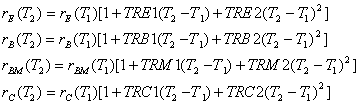
В вышеупомянутых уравнениях, коэффициенты, заканчивающиеся на 1 - температурные коэффициенты первого порядка, заканчивающиеся на 2 – температурные коэффициенты второго порядка для соответствующего параметра.
Скалярный коэффициент AREA позволяет учесть параллельное соединение однотипных транзисторов, для чего в приведенной выше модели БТ изменяются следующие параметры [5]. На параметр AREA необходимо умножить все токи, емкости и заряды, а все сопротивления поделить на AREA. AREAВ и AREAC масштабный размер области базы и области коллектора. AREAВ или AREAC используются для вычисления, и выбирается в зависимости от вертикальной или горизонтальной геометрии (задание параметра модели SUBS). Для вертикальной геометрии AREAВ – масштабный коэффициент (коэффициент пересчета) для IBC, ISC и CJC. Для горизонтальной геометрии масштабный коэффициент AREAC.
Значение AREA указывается в задании на моделирование при включении транзистора в схему, по умолчанию AREA = 1.
Заключение
В результате проведенной работы изучена PSpice модель БТ и параметры для ее описания. В данном проекте были получены основные соотношения для расчета некоторых параметров модели транзистора, зависимости этих параметров от температуры и конструкции, рассмотрены методы экстракции параметров модели из экспериментальных характеристик.
Анализ PSpice модели БТ показал, что наряду с достоинствами этой модели есть и существенные недостатки. В целом модель биполярного транзистора в PSpice может с высокой точностью и в широком диапазоне напряжений, токов и частот описывать характеристики реальных приборов. Но для этого параметры модели должны быть тщательно идентифицированы по достоверным экспериментальным данным. Для идентификации может использоваться входящая в OrCAD 9.2 программа Model Editor. А получение достоверных исходных данных, особенно на высоких частотах, требует применения очень точной измерительной аппаратуры. Поэтому рядовой пользователь обычно не может квалифицированно идентифицировать параметры модели. А использование значений параметров по умолчанию, как было показано выше, не может обеспечить приемлемой точности расчетов.
Автоматическое проектирование ИС распространяется все шире и становится практически единственным инструментом в этой области. Поэтому знание основ модели необходимо для проектировщиков любого уровня.
Список использованных источников
1 Massobrio G., Antognetti P. Semiconductor Device Modeling with SPICE. Second Edition. McGraw-Hill, Inc. 1988. – 479 p.
2 Архангельский А.Я. PSpice и Design Center. В 2-х ч. Часть 1. Схемотехническое моделирование. Модели элементов. Макромоделирование. Учебное пособие. - М.: МИФИ, 1996. - 236 с.
3 Маллер Р., Кейминс Т. Элементы интегральных схем: Пер. с англ. – М.: Мир, 1989. – 630 с., ил.
4 Носов Ю.Р. и др. Математические модели элементов интегральной электроники. - М.: Сов. Радио. 1976. – 304 с.
5 Разевиг В.Д. Система сквозного проектирования электронных устройств Design Lab 8.0. – М.: Солон 1999. – 698 с.
Приложение А
Таблица А - Параметры модели биполярного транзистора
| Обозначение параметра | Параметр | Разме-рность | Значение по умолчанию |
| AF | Показатель степени, определяющий зависимость спектральной плотности фликкер-шума от тока через переход | 1 | |
| BF | Максимальный коэффициент передачи тока в нормальном режиме в схеме с ОЭ (без учета токов утечки) | 100 | |
| BR | Максимальный коэффициент передачи тока в инверсном режиме в схеме с ОЭ | 1 | |
| CJC | Емкость коллекторного перехода при нулевом смещении | Ф | 0 |
| CJE | Емкость эмиттерного перехода при нулевом смещении | пФ | 0 |
| CJS (CCS) | Емкость коллектор-подложка при нулевом смещении | Ф | 0 |
| EG | Ширина запрещенной зоны | эВ | 1,11 |
| FC | Коэффициент нелинейности барьерных емкостей прямосмещенных переходов | 0,5 | |
| GAMMA | Коэффициент легирования эпитаксиальной области | 10-11 | |
| IKF (IK)* | Ток начала спада зависимости BF от тока коллектора в нормальном режиме | А | ∞ |
| IKR* | Ток начала спада зависимости BR от тока эмиттера в инверсном режиме | А | ∞ |
| IRB* | Ток базы, при котором сопротивление базы уменьшается на 50% полного перепада между RB и RBM | А | ∞ |
| IS | Ток насыщения при температуре 27°С | А | 10-16 |
| ISC (C4)* | Ток насыщения утечки перехода база-коллектор | А | 0 |
| ISE (C2)* | Ток насыщения утечки перехода база-эмиттер | А | 0 |
| ISS | Обратный ток p-n-перехода подложки | А | 0 |
| ITF | Ток, характеризующий зависимость TF от тока коллектора при больших токах | А | 0 |
| KF | Коэффициент, определяющий спектральную плотность фликкер-шума | 0 | |
| MJC (МС) | Коэффициент, учитывающий плавность коллекторного перехода | 0,33 | |
| MJE (ME) | Коэффициент, учитывающий плавность эмиттерного перехода | 0,33 | |
| MJS (MS) | Коэффициент, учитывающий плавность перехода коллектор-подложка | 0 | |
| NC* | Коэффициент неидеальности коллекторного перехода | 1,5 | |
| NE* | Коэффициент неидеальности перехода база-эмиттер | 1,5 | |
| NF | Коэффициент не идеальности в нормальном режиме | 1 | |
| NK | Коэффициент, определяющий множитель Qb | 0,5 | |
| NR | Коэффициент неидеальности в инверсном режиме | 1 | |
| NS | Коэффициент неидеальности перехода подложки | 1 | |
| PTF | Дополнительный фазовый сдвиг на граничной частоте транзистора fГР=1/(2Πtf) | градус | 0 |
| QCO | Множитель, определяющий заряд в эпитаксиальной области | Кл | 0 |
| RB | Объемное сопротивление базы (максимальное) при нулевом смещении перехода база-эмиттер | Ом | 0 |
| RBM* | Минимальное сопротивление базы при больших токах | Ом | RB |
| RC | Объемное сопротивление коллектора | Ом | 0 |
| RCO | Сопротивление эпитаксиальной области | Ом | 0 |
| RE | Объемное сопротивление эмиттера | Ом | 0 |
| TF | Время переноса заряда через базу в нормальном режиме | с | 0 |
| TR | Время переноса заряда через базу в инверсном режиме | с | 0 |
| TRB1 | Линейный температурный коэффициент RB | 0C-1 | 0 |
| TRB2 | Квадратичный температурный коэффициент RB | 0C-2 | 0 |
| TRC1 | Линейный температурный коэффициент RC | 0C-1 | 0 |
| TRC2 | Квадратичный температурный коэффициент RC | 0C-2 | 0 |
| TRE1 | Линейный температурный коэффициент RE | 0C-1 | 0 |
| TRE2 | Квадратичный температурный коэффициент RE | 0C-2 | 0 |
| TRM1 | Линейный температурный коэффициент RBM | 0C-1 | 0 |
| TRM2 | Квадратичный температурный коэффициент RBM | 0C-2 | 0 |
| T_ABS | Абсолютная температура | 0C | |
| T_MEASURED | Температура измерений | 0C | |
| T_REL_GLOBAL | Относительная температура | 0C | |
| T_REL_LOCAL | Разность между температурой транзистора и модели-прототипа | 0C | |
| VAF (VA)* | Напряжение Эрли в нормальном режиме | В | ∞ |
| VAR (VB)* | Напряжение Эрли в инверсном режиме | В | ∞ |
| VJC (PC) | Контактная разность потенциалов перехода база-коллектор | В | 0,75 |
| VJE (PE) | Контактная разность потенциалов перехода база-эмиттер | В | 0,75 |
| VJS (PS) | Контактная разность потенциалов перехода коллектор-подложка | В | 0,75 |
| VO | Напряжение, определяющее перегиб зависимости тока эпитаксиальной области | В | 10 |
| VTF | Напряжение, характеризующее зависимость TF от смещения база-коллектор | В | ∞ |
| XCJC | Коэффициент расщепления емкости база-коллектор CJC | 1 | |
| XCJC2 | Коэффициент расщепления емкости база-коллектор CJC | 1 | |
| ХТВ | Температурный коэффициент BF и BR | 0 | |
| XTF | Коэффициент, определяющий зависимость TF от смещения база-коллектор | 0 | |
| ХТI (РТ) | Температурный коэффициент IS | 3 | |
| * Только для модели Гуммеля-Пуна | |||
Похожие работы
... САПРа затраты машинного времени на определение нелинейных функций, описывающих различные полупроводниковые приборы составляют значительную часть общих затрат времени. 1. Проблема математического моделирования биполярных транзисторов Под моделированием понимается описание электрических свойств полупроводникового устройства или группы таких устройств, связанных между собой, с помощью ...
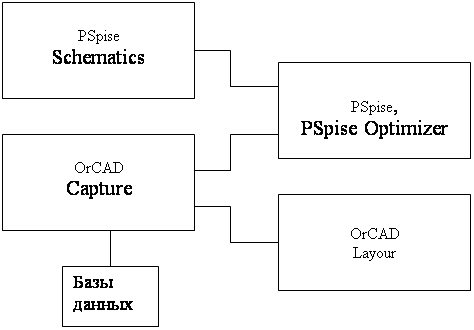
... того пользователь имеет возможность задать любые атрибуты по формату <имя атрибута>=<значение>Допускается рекурсия атрибутов. Этапы создания графической схем в системе автоматизированнного проектирования OrCAD Графический редактор Schematics пакета Design Center 6.2 на платформе Windows позволяет создавать чертежи принципиальных схем и передавать управление программам PSpice, ...
... кафедру для утверждения. После утверждения куратор проекта от кафедры проставляет оценку студенту. ЛИТЕРАТУРА Основная литература 1. Павлов В.Н., Ногин В.Н. Схемотехника аналоговых электронных устройств. М.: Радио и связь, 1997. 2. Ногин В.Н. Аналоговые электронные устройства. М.: Радио и связь, 1992. 304 с. 3. Остапенко Г.С. Усилительные устройства. М.: Радио и связь, 1989. 400 с. ...
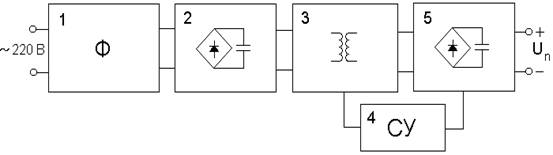
... 2 – управляющее напряжение 2; 3 – выходной сигнал. Рисунок 3.12 – Диаграммы работы буфера управляющего напряжения. Промоделируем динамику работы всей схемы электрической принципиальной (приложение В). Реальный анализ схемы в составе импульсного источника питания в программе проектирования электронных схем не возможен ввиду использования с схеме импульсного трансформатора, модель которого в ...
0 комментариев