Проверка полученной массы состава на трогание с места и по длине приемоотправочных путей

4 Проверка полученной массы состава на трогание с места и по длине приемоотправочных путей

 

Проверка массы состава на трогание. Необходимо проверить выполнение следующего условия:

, (18)

где F_ктр –расчетная сила тяги локомотива при трогании с места, Н;

- удельное сопротивление состава при трогании с места, Н/т;

i_тр - уклон элемента профиля, с которого будет проводиться трогание, ‰. Принимаем, что поезд трогается со станции, которая находится на горизонтальной площадке. Соответственно, i_тр=0 ‰..

Таким образом, масса состава Q не должна превышать значение Q_тр, определенное по условиям трогания поезда на подъеме с уклоном i_тр.

Сопротивление троганию принимают  для подвижного состава на роликовых подшипниках. Здесь q_o – средняя осевая нагрузка, т/ось.

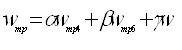, (19)

где α, β, γ–соответственно доля 4-,6- и 8-осных вагонов в составе,

,, - удельное сопротивление соответственно 4-,6- и 8-осных вагонов в составе при трогании с места.

=280/(22+7)=9,6 Н/т;

=280/(21,3+7)=9,8 Н/т;

=280/(21+7)=10 Н/т.

Общее удельное сопротивление троганию состава:

=0,86^.9,6+0,06^.9,8+0,08^.10=9,7 Н/т

Масса состава при трогании с места:

Q_тр=626000/9,7-184=64352 т.

Так как Q<Q_тр, то есть 4700<64352, это значит, что данный локомотив сдвинет с места состав с рассчитанной ранее массой.

Проверка массы состава по длине приемоотправочных путей. Масса состава, рассчитанная по наиболее трудному элементу продольного профиля пути, прошедшая проверки на прохождение более крутого, чем расчетный, подъема и на трогание поезда, может оказаться, тем не менее, слишком большой для того, чтобы поезд уместился в пределах приемоотправочных путей. Для проверки следует определить длину поезда:

где l_л – длина локомотива, м;

l_с – длина состава, м;

10 – допуск на неточность установки поезда в пределах приемо-отправочных путей.

Для определения длины состава необходимо определить число вагонов. Число однотипных вагонов можно рассчитать, если известна, доля массы данной группы вагонов в общей массе состава

, (21)

где  – доля массы i-й группы однотипных вагонов в общей массе состава поезда,

 q_i – средняя масса вагона (брутто) для i-й группы однотипных вагонов.

Округляя n_i до целого и, принимая из ПТР длину одного вагона для рассматриваемой группы, определяют длину состава.

Длина локомотива l_л=33 м,

Длина вагонов:

4-осных l₄=15 м;

6-осных l₆=17 м;

8-осных l₈=20 м.

Число вагонов:

n₄ =0,86^.4700/88=46 вагонов,

n₆=0,06^.4700/128=2 вагонов,

n₈=0,08^.4700/168=2 вагонов.

Длина всего поезда:

l_п=46^.15+2^.17+2^.20+33+10=807 м.

Поскольку в результате расчетов получили длину поезда меньше, чем длину приемоотправочных путей, то корректировать массу поезда не обязательно.

5 Спрямление профиля пути на заданном участке

 

При производстве тяговых расчетов целесообразно заменять несколько малоотличающихся крутизной элементов одним, длина которого S_с равна сумме длин этих элементов. Такую операцию называют спрямлением профиля пути.

Уклон спрямленного элемента определяем по формуле:

(22)

где - уклон спрямляемого элемента, ‰

- длина спрямляемого элемента, м;

- длина спрямленного элемента, м.

Для количественной оценки возможности спрямления профиля вводят условие:

(23)

где =- абсолютное значение разности между уклоном спрямленного участка и действительного значения уклона i-ого элемента, входящий в спрямляемый участок, ‰;

Кривые, имеющиеся на элементах спрямляемого профиля, учитываем с помощью зависимости:

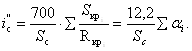
Окончательный уклон спрямленного участника, на котором расположены кривые:

(25)

При спрямлении учитываем условия:

1)    Спрямляем элементы одного знака и 0

Не спрямляем:

2)    Расчетный, максимальный подъем, максимальный спуск и

элементы, на которых располагаются станции.

Результаты спрямления профиля пути приведем в виде таблицы.

Таблица 5.1-Спрямление профиля пути

№ элемента	Длина, м	Уклон, ‰	Кривые			sс, м	iс', ‰	iс", ‰	iс, ‰		Номер приведенного элемента	Примечания
			R, м	sкр, м	aо
1	2000	0	-	-	-	2000	0	0,0	0,0		1	стД
2	450	-3,5	640	-	10	3000				1250	2
3	1750	-6	-	-	-		-5,1	0,1	-5,0	2222
4	800	-4	1500	250	-					1818
5	1000	-2,5	-	-	-	1650	-1,5	0,0	-1,5	2000	3
6	650	0	-	-	-					1333
7	1400	10	-	-	-	1400	10	0,0	10,0		4
8	500	0	-	-	-	1900	3,2	0,2	3,4	625	5
9	800	3	850	400	-					10000
10	600	6	2500	300	-					714
11	1000	0	-	-	-	1000	0	0,0	0,0		6
12	1200	-3,5	1050	600	-	2100	-1,9	0,1	-1,8	1250	7
13	900	-3,5	-	-	-					1176
14	2400	0	-	-	-	2400	0	0,0	0,0		8	стС
15	700	1	1300	400	-	2400	1,3	0,2	1,5	6667	9
16	800	3	-	-	-					1176
17	900	0	1200	-	20					1538
18	4500	8	-	-	-	4500	8	0,0	8,0		10	i
19	375	3	-	-	-	1575	2,2	0,0	2,2	2500	11
20	1200	2	-	-	-					10000
21	4500	0	-	-	-	4500	0	0,0	0,0		12
22	600	-4,5	900	200	-	1800	-6,8	0,2	-6,6	870	13
23	1200	-8	640	-	12					1667
24	1000	0	-	-	-	2700	1,9	0,1	2,0	1053	14
25	900	2	3000	600	-					20000
26	800	4	2000	600	-					952
27	2200	0	-	-	-	2200	0	0,0	0,0		15	cтВ
28	1500	-1,5	-	-	-	1500	-1,5	0,0	-1,5		16
29	4800	-7	1500	900	-	4800	-7	0,1	-6,9		17
30	1500	-2,5	-	-	-	2000	-1,9	0,0	-1,9	3333	18
31	500	0	-	-	-					1053
32	1000	-5,5	860	-	22	1850	-4,8	0,1	-4,7	2857	19
33	850	-4	-	-	-					2500
34	600	0	750	-	15	2300	-1,7	0,2	-1,5	1176	20
35	700	-2	-	-	-					6667
36	600	-3,5	-	-	-					1111
37	400	-1	640	250	-					2857
38	2000	0	-	-	-	2000	0	0,0	0,0		21	стА

Приведем пример спрямления участка на основании элементов №2,№3 и № 4.

Длина спрямленного участка вычисляется по формуле:

(26)

где , и  - длина 2-ого, 3-его и 4-ого элемента спрямляемого участка, м;

 м;

Уклон спрямленного элемента определяем по формуле (22):

 ‰.

Для учета на профиле кривых воспользуемся формулой (24):

 ‰,

 ‰,

 ‰.

Окончательный уклон определяем по формуле (25):

 ‰.

Определим, удовлетворяют ли значения длин наших элементов условию возможности спрямления:

 м< м;

м<  м;

м<  м.

Так как условие возможности спрямления выполнилось, значит, элементы № 2, №3 и №4 можно спрямить.

Аналогичным образом производятся спрямления других элементов.