Навигация
1. Ům=Rİm 3. Ům=jωCİm
Закон Ома в комплексной форме для индуктивности:
Ům=jωLİm
Среднее значение мгновенной мощности за период синусоидального тока в цепях с идеальными емкостями и индуктивностями равно ui В идеальном источнике э. д. с. постоянное значение имеет напряжение Если напряжение на конденсаторе во времени постоянно, то ток через нее изменяется по закону:
он равен нулю.
Если напряжение на конденсаторе возрастает по квадратичному закону, то ток через нее изменяется по закону:
Квадратичному Если напряжение на конденсатор возрастает во времени линейно, то ток через нее изменяется по закону:
Линейному Если ток через конденсатор протекает во времени постоянный, то напряжение на нем изменяется по закону:
Остается постоянным.
Если ток через конденсатор возрастает во времени линейно, то напряжение на нем изменяется по закону:
Линейному Если напряжение на индуктивности линейно возрастает во времени, то напряжение на ней изменяется по закону:
Линейному Если ток через индуктивность линейно возрастает во времени, то напряжение на ней изменяется по закону:
Линейному Если ток через индуктивность линейно возрастает во времени, то напряжение на ней изменяется по закону:
Линейному Если ток через индуктивность линейно возрастает во времени, то напряжение на ней изменяется по закону:
Линейному Если ток через индуктивность линейно возрастает во времени, то напряжение на ней изменяется по закону:
Линейному Внутреннее сопротивление (Ri) идеального источника эдс равно:
Ri = 0
Внутреннее сопротивление (Ri) идеального источника тока равно:
Ri® ∞
Между индуктивно связанными элементами связь:
магнитная.
Реальный индуктивно связанный элемент называется:
Трансформатор.
Основное назначение трансформатора:
Преобразование амплитуды напряжения переменного тока или напряжения.
Мгновенный ток через конденсатор с емкостным сопротивлением Xc=10 Ом при мгновенном значении напряжения на нем uC=20sin(ωt+φ) равен:
iC=2sin(ωt+φ - π/2).
Комплексная амплитуда тока через конденсатор с емкостным сопротивлением Xc=10 Ом при мгновенном значении напряжения на нем uC=20sin(ωt+φ) равна:
IC=2ejφ.
Мгновенное напряжение на катушкe индуктивности с индуктивным сопротивлением XL =10 Ом при токе через индуктивность iL=12sin(ωt+φ) равно:
2. uL=120sin(ωt + φ+ π/2)
Комплексная амплитуда напряжения на катушкe индуктивности с индуктивным сопротивлением XL =10 Ом при заданном токе через индуктивность iL=12sin(ωt+φ) равна:
2. uL=120ej(φ + π/2)
4. uL=120ej(φ - π/2).
Мгновенное напряжение на сопротивлении R =10 Ом при заданном токе i=12sin(ωt+φ).
1. u=120sin(ωt + φ)
Комплексная амплитуда напряжения на сопротивлении R =10 Ом при заданном токе i=15sin(ωt+φ) равна:
4. u=150ejφ.
Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно:
u=1,2sin(ωt + φ)
4. Электрические цепи при гармоническом воздействии в установившемся режимеОсновные свойства линейных цепей:
Принципа суперпозиции.
Независимыми называют узлы, которые:
отличаются одной ветвью.
Независимыми называются контура, которые:
отличаются одной ветвью.
Число независимых узлов определяется из соотношения:
NУ= у-1
Число независимых контуров определяется из соотношения:
Nк= в-у+1.
Показать запись закона Ома в комплексной форме.
Ům=Zİm.
Показать запись первого закона Кирхгофа в комплексной форме:
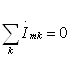
Показать запись второго закона Кирхгофа в комплексной форме:
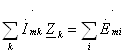
На каком законе основан метод контурных токов.
2-ой закон Кирхгофа.
На каком законе основан метод узловых потенциалов.
1-ый закон Кирхгофа.
Записать уравнения по методу токов ветвей (рис.1.5):
| 1. |
| (Z1+Z2) I1+Z3 I2=u1 Z3I1+(Z2+Z3 +Z4) I2=0 |
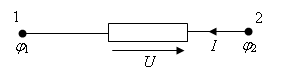
Запишите первый закон Кирхгофа (для узла А на рис.1).
I2+I3-I4-I5=0
Запишите второй закон Кирхгофа (для контура J1 на рис.1).
I3R2+I4R3 =E.
Для элементов соединенных последовательно общим является:
Ток.
Для элементов соединенных параллельно общим является:
Напряжение.
Эквивалентное сопротивление трех параллельно соединенных резисторов с одинаковым сопротивлением, равным 3 Ома, равно:
Похожие работы
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... можно строить схемы замещения реальных элементов цепи. 3. Топологические элементы схем Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи. Основные понятия: 1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток. 2) Узел – место соединения трех и более ветвей ...






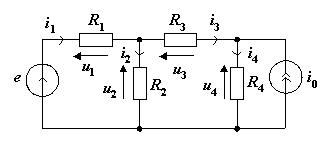

0 комментариев