ImL>ImC.3. ImL<ImC

2. ImL>ImC.3. ImL<ImC.

Амплитуды токов через реактивные элементы в параллельном колебательном контуре на резонансной частоте находятся в соотношении:

ImL=ImC

Амплитуды напряжений на реактивных элементах в последовательном колебательном контуре на резонансной частоте находятся в соотношении:

UmL=UmC

Число частотных характеристик электрической цепи:

равно, числу параметров электрической цепи.

Амплитуды напряжений на реактивных элементах в параллельном колебательном контуре на резонансной частоте находятся в соотношении:

2. UmL>UmC.3. UmL<UmC.

Число параметров и частотных характеристик двухполюсника равно:

два

Число параметров и частотных характеристик четырехполюсника равно:

двенадцать

Фазовый сдвиг между напряжением и током на резонансной частоте на входе последовательного колебательного контура:

j=0

Характеристическое сопротивление колебательного контура показывает:

1. сопротивление источника сигнала.

2. сопротивление реактивного элемента на резонансной частоте.

3. сопротивление реактивного элемента на частоте воздействующего сигнала.

4. сопротивление резистивных потерь контура:

Напряжение на реактивных элементах последовательного колебательного контура на резонансной частоте равно:

Ux=Imr

Фазовый сдвиг между напряжением и током на резонансной частоте на входе параллельного колебательного контура:

1. j=0.2. j>0.3. j<0.

При подключении резистора параллельно с конденсатором последовательного колебательного контура его добротность:

увеличится.

При подключении резистора последовательно с элементами последовательного колебательного контура его добротность:

уменьшится.

При подключении резистора параллельно с конденсатором параллельного колебательного контура его добротность:

уменьшится.

Для максимальной добротности последовательного контура сопротивление источника сигнала Ri и сопротивление нагрузки Rн должны удовлетворять условиям:

Ri=0, Rн→∞.

Для максимальной добротности параллельного контура сопротивление источника сигнала Ri и сопротивление нагрузки Rн должны удовлетворять условиям:

Ri=→∞, Rн→∞.

Добротность Q, полоса пропускания S и резонансная частота f0 контура связаны соотношением:

Q=f0/S

Собственные колебания медленнее затухают в колебательном контуре:

1. Узкополостном.

2. Широкополостном.

3. Затухание не зависит от полосы пропускания колебания контура.

Большей добротностью обладает колебательный контур:

1. узкополосный.

2. широкополосный.

4. их добротность одинакова.

Сопротивление последовательного колебательного контура на резонансной частоте:

резистивное, минимальной величины.

Резонанс в последовательном колебательном контуре называется резонансом:

напряжений

Резонанс в параллельном колебательном контуре называется резонансом:

токов

Характер сопротивления последовательного контура на частоте меньше резонансной:

емкостной.

Характер сопротивления последовательного контура на частоте равной резонансной:

резистивный.

Сопротивления последовательного контура на частоте больше резонансной имеет характер:

Индуктивный.

Сопротивления параллельного контура на частоте меньше резонансной имеет характер:

Индуктивный.

Сопротивления параллельного контура на частоте больше резонансной имеет характер:

Емкостное.

Сопротивление параллельного контура на резонансной частоте:

Резистивное, максимальной величины.

Каково назначение колебательных контуров частотная избирательность.

Избирательность колебательного контура определяется:

полосой пропускания.

В электротехнике под резонансом понимают не амплитудный, а фазовый потому что:

Амплитуды напряжений на реактивных элементах достигают максимума на разных частотах.

Под фазовым резонансом для цепи с комплексным сопротивлением Z=R+jX понимают:

условие, при котором напряжение и ток находятся в одной фазе.

Под термином амплитудный резонанс понимают:

Резкое увеличение амплитуды тока или напряжения на резонансной частоте на элементах цепи по отношению к амплитуде на других частотах;

В колебательном контуре обязательно присутствуют:

конденсатор и катушка индуктивности.

Термин "обобщенная расстройка колебательного контура" означает:

а= (ωL – 1/(ωC)) /R ≈ Q2Δω/ω0.

Термин "абсолютная расстройка колебательного контура" означает:

Δω=ω – ω0.

Термин "относительная расстройка колебательного контура" означает:

δω=(ω – ω0) /ω0. . = Δω/ω0.

6. Импульсные сигналы в линейных цепях

Переходной процесс в электрической цепи связан:

с изменением энергетического состояния энергоемких элементов.

2. Показать запись законов коммутации для реактивных элементов:

IL(-0) = IL(+0),. Uc(-0) = Uc(+0).

3. Переходная характеристика электрической цепи это:

Отклик на единичное ступенчатое воздействие.

Колебательным контуром называется цепь:

1. в которой параметры элементов изменяются по гармоническому закону.

2. переходная характеристика которой, изменяется по гармоническому закону.

3. на которую воздействует гармонический сигнал.

От чего зависит характер переходной характеристики (апериодический, колебательный, критический).

1. Добротности.

2. Резонансной частоты.

3. Характеристического сопротивления.

Операторная функции цепи К(р) связана с комплексной частотной характеристике К(jω) с помощью:

Замены р на jω.

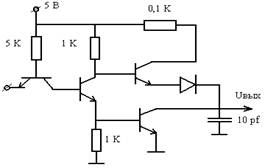
Нарисовать схему замещения цепи (рис.3) при ω→0.

2

Нарисовать схему замещения цепи (рис.3) при ω→∞.

1

Нарисовать схему замещения цепи (рис.3) при ступенчатом входном сигнале когда t→∞.

2

Нарисовать схему замещения цепи (рис.3) при ступенчатом входном сигнале когда t→0.

1

На вход цепи (рис.3) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→∞:

0

На вход цепи (рис.3) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→0:

E R2/(R1+R2)

На вход цепи (рис.3) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0:

0

На вход цепи (рис.3) воздействует ступенчатое напряжение. Рассчитать вы ходное напряжение при t→∞:

E R2/(R1+R2)

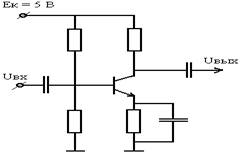
Нарисовать схему замещения цепи (Рис.6а) при ω→0:

2

Нарисовать схему замещения цепи (Рис.6а) при ω→∞:

3

Нарисовать схему замещения цепи (Рис.6а) при t→∞.

2

Нарисовать схему замещения цепи (Рис.6а) при t→0.

3

На вход цепи (Рис.6а) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0:

E R1/(R1+R2)

На вход цепи (Рис.6а) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→∞:

E R2/(R1+R2)

На вход цепи (Рис.6а) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→0

E R2/(R1+R2)

На вход цепи (Рис.6а) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→∞

E R1/(R1+R2)

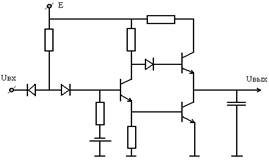
Нарисовать схему замещения цепи (рис.13) при ω→0.

2

Нарисовать схему замещения цепи (рис.13) при ω→∞.

3

Нарисовать схему замещения цепи (рис.13) при t→∞.

2

Нарисовать схему замещения цепи (рис.13) при t→0:

3

На вход цепи (рис.13) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0:

E R1/(R1+R2)

На вход цепи (рис.13) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→∞:

E R2/(R1+R2)

На вход цепи (рис.13) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→0:

E R2/(R1+R2)

На вход цепи (рис.13) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→∞:

E R1/(R1+R2)

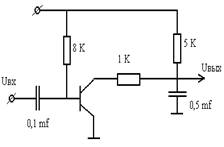
Нарисовать схему замещения цепи (рис.16) при ω→0.

2

Нарисовать схему замещения цепи (рис.16) при ω→∞.

3

Нарисовать схему замещения цепи (рис.16) при t→∞.

2

Нарисовать схему замещения цепи (рис.16) при t→0.

3

На вход цепи (рис.16) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0.

E R1/(R1+R2)

На вход цепи (рис.16) воздействует ступенчатое напряжение. Рассчитать вы ходное напряжение при t→∞.

E R2/(R1+R2)

На вход цепи (рис.16) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→∞.

E R1/(R1+R2)

На вход цепи (рис.16) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→0

E R2/(R1+R2)

Нарисовать схему замещения цепи (рис.14) при ω→0.

3

Нарисовать схему замещения цепи (рис.14) при ω→∞.

2

Нарисовать схему замещения цепи (рис.14) при t→∞.

3

Нарисовать схему замещения цепи (рис.14) при t→0.

2

На вход цепи (рис.14) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0.

E R2/(R1+R2)

На вход цепи (рис.14) воздействует ступенчатое напряжение. Рассчитать вы ходное напряжение при t→∞.

E R1/(R1+R2)

На вход цепи (рис.14) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→∞.

E R2/(R1+R2)

На вход цепи (рис.14) воздействует гармоническое напряжение Ecosωt. Рассчитать амплитуду выходного напряжение при ω→0

E R1/(R1+R2)

Переходные процессы в линейных электрических цепях первого порядка описываются:

нелинейными дифференциальными уравнениями первого порядка;

Закон коммутации в электрической цепи с индуктивностью записываются в виде:

1) iL(0+) = iL(0-);

Закон коммутации в электрической цепи с емкостью имеет следующий вид:

uс(0+) = uс(0-)

Переходный процесс установления тока в электрической цепи первого порядка описывается выражением 1) i=A1e P1 t + A2e P2 t; 2) i=iуст. + Ae P t +; 3) i= A1e P1 t

Постоянная времени интегрирующей RC-цепи определяется выражением t=RC

Постоянная времени интегрирующей RL-цепи определяется выражением t=L/R.

Переходные процессы в линейных электрических цепях второго порядка описываются:

нелинейными дифференциальными уравнениями первого порядка;

Операторный (операционный) метод анализа электрических цепей основан на:

Преобразование Лапласа;

Если для дифференцирующей RC-цепи длительность импульса много меньшей, чем постоянная времени цепи, то цепь называется: