Навигация
3. KN(jω) =F [Ki(jω)]
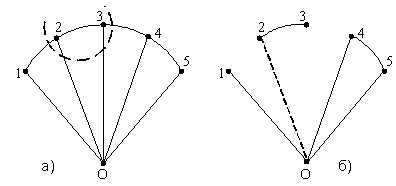
Как рассчитывается комплексный коэффициент передачи N-звенного фильтра если звенья одинаковы, обладают комплексным коэффициентом передачи Ki(jω), но не согласованы по напряжениям.
1. KN(jω) =![]() .
.
2. KN(jω) =![]() .
.
3. KN(jω) =F [Ki(jω)]
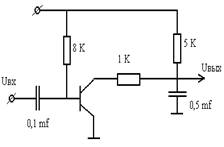
К какой группе фильтров относятся схемы, приведенные на рисунках:

ФНЧ
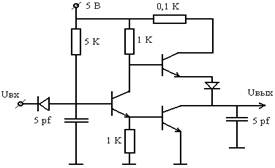
К какой группе фильтров относятся схемы, приведенные на рисунках:

ФВЧ
К какой группе фильтров относятся схемы, приведенные на рисунках:

ПФ
К какой группе фильтров относятся схемы, приведенные на рисунках:
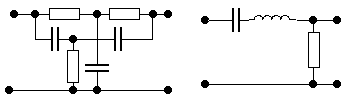
РФ
9. Цепи с распределенными параметрамиПод термином "цепи с распределенными параметрами" понимают:
1. Цепи, геометрические размеры элементов которых соизмеримы или больше длины электромагнитной волны сигнала, проходящего по ним;
2. цепи, геометрические размеры отдельных элементов которых много меньшие длины электромагнитной волны сигнала, проходящего по ним;
3. цепи, в которых отдельные элементы могут выполнять ряд различных функций;
2. Под термином "цепи с сосредоточенными параметрами" понимают:
1. Цепи, геометрические размеры элементов которых соизмеримы или больше длины электромагнитной волны сигнала, проходящего по ним;
2. цепи, геометрические размеры отдельных элементов которых много меньшие длины электромагнитной волны сигнала, проходящего по ним;
3. цепи, в которых отдельные элементы могут выполнять ряд различных функций;
3. Волна от источника сигнала в бесконечной длинной линии распространяется в:
1. В обе стороны от источника;
2. в направлении перпендикулярном длинной линии;
3. в одну сторону от источника сигнала;
Волна от источника сигнала в полубесконечной длинной линии распространяется в:
1. В обе стороны;
2. в направлении перпендикулярном длинной линии;
3. в одну сторону;
Под термином "длинная линия" понимают:
1. линию связи, которую необходимо рассматривать как цепь с распределенными параметрами.
2. линию связи, которую необходимо рассматривать как цепь с сосредоточенными параметрами.
3. цепи, геометрические размеры отдельных элементов которых много меньшие длины электромагнитной волны сигнала, проходящего по ним;
Длинную линию называют однородной если:
1. погонные параметры зависят от координаты х;
2. погонные параметры не зависят от координаты х;
3. погонные параметры зависят от времени;
4. погонные параметры не зависят от времени.
Длинную линию называют неоднородной если:
1. погонные параметры зависят от координаты х;
2. погонные параметры не зависят от координаты х;
3. погонные параметры зависят от времени;
4. погонные параметры не зависят от времени.
В длинной линии без потерь погонные параметрыe удовлетворяют условиям:
1. L0=G0=0, 2. C0=R0=0, 3. R0=G0=0, 4. R0 >0, G0. >0, В длинной линии с потерями погонные параметры удовлетворяют условиям:
1. L0=G0=0, 2. R0=G0=0, 3. R0 >0, G0. >0, 4. L0=C0=0.
В бесконечной длинной линии возникает:
1. Две волны: падающая и отраженная;
2. Две волна: прямая и обратная;
3. Одна волна – падающая;
4. Одна волна – отраженная.
В полубесконечной длинной линии возникает:
1. Две волны: падающая и отраженная;
2. Две волна: прямая и обратная;
3. Одна волна – падающая;
4. Одна волна – отраженная.
В длинной линии конечной длины возникает:
1. Две волны: падающая и отраженная;
2. Две волна: прямая и обратная;
3. Одна волна – падающая;
4. Одна волна – отраженная.
К волновым параметрам длинной линии относятся:
1. Погонные.
2. Волновое число, волновое сопротивление, коэффициент распространения.
3. Коэффициент бегущей волны и коэффициент стоячей волны.
4. Коэффициенты отражения
К первичным параметрам длинной линии относятся:
1. Погонные.
2. Волновые.
3. Коэффициент бегущей волны и коэффициент стоячей волны.
4. Коэффициенты отражения.
К вторичным параметрам длинной линии относятся:
1. Погонные.
2. Волновые.
3. Коэффициент бегущей волны и коэффициент стоячей волны.
4. Коэффициенты отражения.
К погонным параметрам длинной линии относятся:
1. параметры, отнесенные к единице длины линии.
2. Волновые.
3. Коэффициент бегущей волны и коэффициент стоячей волны.
4. Коэффициенты отражения.
Вследствие интерференции падающей и отраженной волн возникает:
1. Изменение частоты отраженной волны;
2. Узлы и пучности;
3. Изменение направления распространения отраженной волны.
В полубесконечной длинной линии возникает режим:
1. бегущих волн;
2. отраженных волн;
3. поглощенных волн;
4. стоячих волн;
В линии конечной длины при работе на согласованную нагрузку возникает режим:
1. бегущих волн;
2. Режим отраженных волн;
3. Режим поглощенных волн;
4. Режим стоячих волн;
В линии конечной длины, работающей на короткозамкнутую нагрузку, возникает режим:
1. бегущих волн;
2. отраженных волн;
3. поглощенных волн;
4. стоячих волн;
В нагрузке максимальная мощность сигнала выделяется в режиме:
1. бегущих волн;
2. отраженных волн;
3. поглощенных волн;
4. стоячих волн;
В каком режиме в длинной линии отсутствуют отражения 1. В режиме стоячих волн.
2. В режиме бегущих волн.
3. В режиме смешанных волн.
4. В режиме стоячих волн и бегущих волн.
В длинной линии без потерь конечной длины режим бегущих волн возникает, когда нагрузка:
1. Резистивная и равна волновому сопротивлению линии.
2. Комплексная.
3. Индуктивная.
4. Резистивная, меньшей волнового сопротивления линии.
5. Резистивная, большей волнового сопротивления линии.
В длинной линии без потерь конечной длины возникает режим смешанных волн, когда нагрузка:
1. Резистивная и равна волновому сопротивлению линии.
2. Комплексная или резистивная не равная волновому сопротивлению.
3. Реактивная.
В длинной линии без потерь конечной длины возникает режим стоячих волн, когда нагрузка:
1. Резистивная и равна волновому сопротивлению линии.
2. Комплексная.
3. Реактивная.
4. Резистивная, меньшей волнового сопротивления линии.
5. Резистивная, большей волнового сопротивления линии.
Коэффициентом отражения по напряжению называется:
1. рu=Ủотр/Ủпад.
2. К = Um min/ Um max
3. рu= Ủпад/ Ủотр.
4. К = Um max /Um min
Коэффициентом бегущей волны называется:
1. рu=Ủотр/Ủпад.
2. К = Um min/ Um max
3. рu= Uпад/ Uотр.
4. К = Um max /Um min
Коэффициентом стоячей волны называется:
1. рu=Ủотр/Ủпад.
2. К = Um min/ Um max
3. рu= Uпад/ Uотр.
4. К = Um max /Um min
Коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии нагруженной на волновое сопротивление равны:
1. КБВ=1, рu=1.
2. КБВ=0, рu=0.
3. КБВ=0, рu=1.
4. КБВ=1, рu=0.
Коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии в режиме бегущих волн равны:
1. КБВ=1, рu=1.
2. КБВ=0, рu=0.
3. КБВ=0, рu=1.
4. КБВ=1, рu=0.
Коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии разомкнутой на конце равны:
1. КБВ=1, рu=1.
2. КБВ=0, рu=0.
3. КБВ=0, рu=1.
4. КБВ=1, рu=0.
5. КБВ=0, рu=-1.
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии в режиме стоячих волн.
1. КБВ=1, рu=1.
2. КБВ=1, рu=0.
3. КБВ=0, рu=1.
4. КБВ=1, рu=0.
5. КБВ=1, рu=-1.
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии короткозамкнутой на конце.
1. КБВ=1, рu=1.
2. КБВ=0, рu=0.
3. КБВ=0, рu=1.
4. КБВ=1, рu=0.
5. КБВ=0, рu=-1.
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии нагруженной на реактивное сопротивление.
1. КБВ=1, рu=1.
2. КБВ=1, рu=1.
3. КБВ=0, рu=1.
4. КБВ=0, рu= а+ jb.
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии в режиме смешанных волн.
1.0<КБВ<1, | рu | <1.
2. КБВ=1, рu=1.
3. КБВ=1, рu=1.
4. КБВ=0, рu=а+ jb
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии нагруженной на резистивное сопротивление больше волнового.
1.0<КБВ<1, | рu | <1.
2. КБВ=1, рu=1.
3. КБВ=1, рu=1.
4. КБВ=0, рu=а+ jb
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии нагруженной на резистивное сопротивление меньше волнового.
1.0<КБВ<1, | рu | <1.
2. КБВ=1, рu=1.
3. КБВ=1, рu=1.
4. КБВ=0, рu=а+ jb
Чему равны коэффициент бегущей волны (КБВ) и коэффициент отражения по напряжению рu в линии нагруженной на комплексное сопротивление.
1.0<КБВ<1, | рu | <1.
2. КБВ=1, рu=1.
3. КБВ=1, рu=1.
4. КБВ=0, рu=а+ jb
Похожие работы
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... можно строить схемы замещения реальных элементов цепи. 3. Топологические элементы схем Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи. Основные понятия: 1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток. 2) Узел – место соединения трех и более ветвей ...







0 комментариев