Навигация
Интегралы свертки (наложения)
9694
знака
0
таблиц
7
изображений
4. Интегралы свертки (наложения)
Рассмотрим порядок определения реакции линейной электрической цепи на сложное воздействие, если известна импульсная характеристика этой цепи 
. Будем считать, что воздействие представляет собой кусочно-непрерывную функцию 
, показанную на рисунке 7.
Рис. 7
Пусть требуется найти значение реакции 
в некоторый момент времени 
. Решая эту задачу, представим воздействие в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени 
, показан на рисунке 7. Этот импульс характеризуется длительностью 
и высотой 
.
Из ранее рассмотренного материала известно, что реакцию цепи на короткий импульс можно считать равной произведению импульсной характеристики цепи на площадь импульсного воздействия. Следовательно, бесконечно малая составляющая реакции, обусловленная этим импульсным воздействием, в момент времени 
будет равной:
,
поскольку площадь импульса равна 
, а от момента его приложения до момента наблюдения проходит время 
.
Используя принцип наложения, полную реакцию цепи 
можно определить как сумму бесконечно большого числа бесконечно малых составляющих 
, вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени .
Таким образом:
.
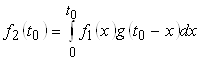Эта формула верна для любых значений , поэтому обычно переменную обозначают просто 
. Тогда:
.
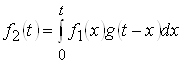Полученное соотношение называют интегралом свертки или интегралом наложения. Функцию , которая находится в результате вычисления интеграла свертки, называют сверткой и .
Можно найти другую форму интеграла свертки, если в полученном выражении для осуществить замену переменных:
.
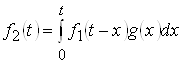Пример: найти напряжение на емкости последовательной 
-цепи (рис. 8), если на входе действует экспоненциальный импульс вида:
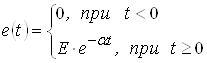
Рис. 8
Воспользуемся интегралом свертки:
.
Выражение для 
было получено ранее.
Следовательно, 
, и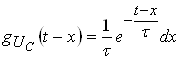 
.
Тогда
Такой же результат можно получить, применив интеграл Дюамеля.
Литература:
Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. (Учебник)
Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998. (Учебник);
Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974. (Учебник);
Попов В. П. Основы теории цепей – М.: Высшая школа, 2000.(Учебник)
Похожие работы
... 5. Расчет частотных характеристик ПФ Построение АЧХ и ФЧХ по карте нулей и полюсов. 0 0 0 0 0 0 АЧХ: ФЧХ: 6. Временные характеристики Временными характеристиками электрической цепи ...
... не совпадает с началом отсчета времени, то интеграл (8.12) принимает вид Интегралы наложения (8.12) и (8.13) представляют собой свертку входного сигнала с импульсной характеристикой цепи и широко применяются в теории электрических цепей и теории передачи сигналов. Ее физический смысл заключается в том, что вход ной сигнал f1(t) как бы взвешивается с помощью функции h(t—t): чем медленнее ...
... пример анализа переходных процессов операторным методом, основанный на теоретических знаниях. В результате чего произведено более глубокое и эффективное изучение материала по теме: «Анализ переходных процессов в электрических цепях», а также освоение новых программ и приложений, требуемых при построении схем, графиков и расчёте формул. 1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 1.1 ...
... K(p) - операторный коэффициент передачи цепи 2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студенту группы 9341 Прокопьева К.В. Учебная дисциплина “Радиотехнические цепи и сигналы” 2.1 Тема работы Анализ радиотехнических сигналов и их прохождение через линейные цепи. 2.2 Цель работы Анализ радиотехнических сигналов и линейных цепей методами математического ...
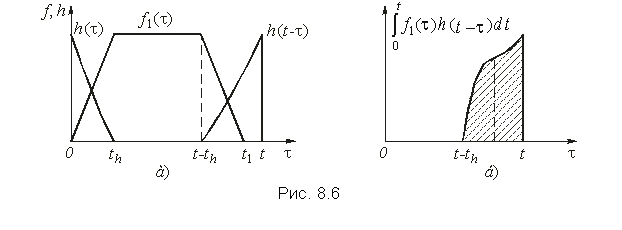
0 комментариев