Понятие о физической величине. Международная система единиц физических величин СИ

1. ПОНЯТИЕ О ФИЗИЧЕСКОЙ ВЕЛИЧИНЕ. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН СИ

Под физической величиной понимают характеристику физических объектов или явлений материального мира, общую в качественном отношении для множества объектов или явлений, но индивидуальную для каждого из них в количественном отношении. Например, масса – физическая величина. Она является общей характеристикой физических объектов в качественном отношении, но в количественном отношении для различных объектов имеет свое индивидуальное значение.

Под значением физической величины понимают ее оценку, выражаемую произведением отвлеченного числа на принятую для данной физической величины единицу. Например, в выражении для давления атмосферного воздуха р = 95,2 кПа, 95,2 – отвлеченное число, представляющее числовое значение давления воздуха, кПа – принятая в данном случае единица давления.

Под единицей физической величины понимают физическую величину, фиксированную по размеру и принятую в качестве основы для количественной оценки конкретных физических величин. Например, в качестве единиц длины применяют метр, сантиметр и др.

Одной из важнейших характеристик физической величины является ее размерность. Размерность физической величины отражает связь данной величины с величинами, принятыми за основные в рассматриваемой системе величин.

Система величин, которая определяется Международной системой единиц СИ и которая принята в России, содержит семь основных системных величин, представленных в Табл.1.1.

Существуют две дополнительные единицы СИ – радиан и стерадиан, характеристики которых представлены в Табл.1.2.

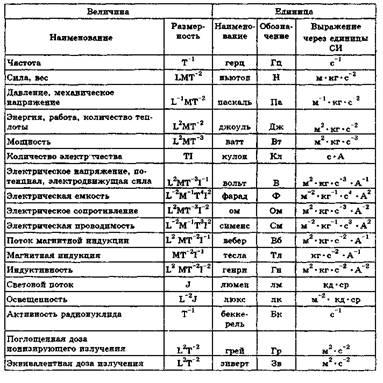
Из основных и дополнительных единиц СИ образованы 18 производных единиц СИ, которым присвоены специальные, обязательные к применению наименования. Шестнадцать единиц названы в честь ученых, остальные две – люкс и люмен (см. Табл.1.3).

Специальные наименования единиц могут быть использованы при образовании других производных единиц. Производными единицами, не имеющими специального обязательного наименования являются: площадь, объем, скорость, ускорение, плотность, импульс, момент силы и др.

Наравне с единицами СИ допускается применять десятичные кратные и дольные от них единицы. В Табл.1.4 представлены наименования и обозначения приставок таких единиц и их множители. Такие приставки называются приставками СИ.

Выбор той или иной десятичной кратной или дольной единицы прежде всего определяется удобством ее применения на практике. В принципе выбирают такие кратные и дольные единицы, при которых числовые значения величин находятся в диапазоне от 0,1 до 1000. Например, вместо 4000000 Па лучше применять 4 МПа.

Таблица 1.1. Основные единицы СИ

Величина			Единица				Обозначения рекомендуемых кратных и дольных единиц
Наименование	Размерность	Рекомендуемое обозначение	Наименование	Обозначение		Определение
				международное	русское
Длина	L	l	метр	m	м	Метр равен расстоянию, проходимому в вакууме плоской электромагнитной волной за 1/299792458 долей секунды	км, см, мм, мкм, нм
Масса	М	m	килограмм	kg	кг	Килограмм равен массе международного прототипа килограмма	Мг, г, мг, мкг
Время	Т	t	секунда	s	с	Секунда равна 9192631770 периодам излучения при переходе между двумя сверхтонкими уровнями основного состояния атома цезия-133	кс, мс, мкс, нс
Сила электрического тока	I	I	ампер	А	А	Ампер равен силе изменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия 2·10-7 Н	кА, мА, мкА, нА, пА
Термодинамическая температура		T	кельвин*	К	К	Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды	МК, кК, мК, мкК
Количество вещества	N	n; n	моль	mol	моль	Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг	кмоль, ммоль, мкмоль
Сила света	J	J	кандела	cd	кд	Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частостей 540·1012 Гц, сила излучения которого в этом направлении составляет 1/683 Вт/ср

* Кроме температуры Кельвина (обозначение Т) допускается применять также температуру Цельсия (обозначение t), определяемую выражением t = Т – 273,15 К. Температура Кельвина выражается в кельвинах, а температура Цельсия – в градусах Цельсия (°С). Интервал или разность температур Кельвина выражают только в кельвинах. Интервал или разность температур Цельсия допускается выражать как в кельвинах, так и в градусах Цельсия.

Таблица 1.2

Дополнительные единицы СИ

Величина			Единица					Обозначения рекомендуемых кратных и дольных единиц
Наименование	Размерность	Рекомендуемое обозначение	Определяющее уравнение	Наименование	Обозначение		Определение
					международное	русское
Плоский угол	1	a, b, g, q, n, j	a = s/r	радиан	rad	рад	Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу	мрад, мкрад
Телесный угол	1	w, W	W = S/r2	стерадиан	sr	ср	Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы

Таблица 1.3

Производные единицы СИ, имеющие специальные наименования

Величина		Единица
Наименование	Размерность	Наименование	Обозначение
			международное	русское
Частота	Т-1	герц	Hz	Гц
Сила, вес	LMT-2	ньютон	N	Н
Давление, механическое напряжение, модуль упругости	L-1MT-2	паскаль	Pa	Па
Энергия, работа, количество теплоты	L2MT-2	джоуль	J	Дж
Мощность, поток энергии	L2MT-3	ватт	W	Вт
Электрический заряд (количество электричества)	ТI	кулон	С	Кл
Электрическое напряжение, электрический потенциал, разность электрических потенциалов, электродвижущая сила	L2MT-3I-1	вольт	V	В
Электрическая емкость	L-2M-1T4I2	фарад	F	Ф
Электрическое сопротивление	L2MT-3I-2	ом		Ом
Электрическая проводимость	L-2M-1T3I2	сименс	S	См
Поток магнитной индукции, магнитный поток	L2MT-2I-1	вебер	Wb	Вб
Плотность магнитного потока, магнитная индукция	MT-2I-1	тесла	Т	Тл
Индуктивность, взаимная индуктивность	L2MT-2I-2	генри	Н	Гн
Световой поток	J	люмен	lm	лм
Освещенность	L-2J	люкс	lx	лк
Активность нуклида в радиоактивном источнике	T-1	беккерель	Bq	Бк
Поглощенная доза излучения, керма	L2T-2	грей	Gy	Гр
Эквивалентная доза излучения	L2T-2	зиверт	Sv	Зв

Таблица 1.4

Наименования и обозначения приставок СИ для образования десятичных кратных и дольных единиц и их множители

Наименование приставки	Обозначение приставки		Множитель
	международное	русское
экса	E	Э	1018
пета	P	П	1015
тера	T	Т	1012
гига	G	Г	109
мега	M	М	106
кило	k	к	103
гекто*	h	г	102
дека*	da	да	101
деци*	d	д	10-1
санти*	c	с	10-2
милли	m	м	10-3
микро		мк	10-6
нано	n	н	10-9
пико	p	п	10-12
фемто	f	ф	10-15
атто	a	а	10-18

* Приставки "гекто", "дека", "деци" и "санти" допускается применять только для единиц, получивших широкое распространение, например: дециметр, сантиметр, декалитр, гектолитр.

МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ С ПРИБЛИЖЕННЫМИ ЧИСЛАМИ

В результате измерений, а также при проведении многих математических операций получаются приближенные значения искомых величин. Поэтому необходимо рассмотреть ряд правил вычислений с приближенными значениями. Эти правила позволяют уменьшить объем вычислительной работы и исключить дополнительные погрешности. Приближенные значения имеют такие величины, как , логарифмы и т. п., различные физические постоянные, результаты измерений.

Как известно, любое число записывают с помощью цифр: 1, 2, …, 9, 0; при этом значащими цифрами считают 1, 2, …, 9. Нуль может быть как значащей цифрой, если он стоит в середине или конце числа, так и незначащей, если он стоит в десятичной дроби с левой стороны и указывает лишь разряд остальных цифр.

При записи приближенного числа следует учитывать, что цифры, составляющие его, могут быть верными, сомнительными и неверными. Цифра верна, если абсолютная погрешность числа меньше одной единицы разряда этой цифры (слева от нее все цифры будут верными). Сомнительной называют цифру, стоящую справа от верной цифры, а цифры справа от сомнительной неверные. Неверные цифры необходимо отбросить не только в результате, но и в исходных данных. Округлять число при этом не нужно. Когда погрешность числа не указана, то следует считать, что абсолютная погрешность его равна половине единицы разряда последней цифры. Разряд старшей цифры погрешности показывает разряд сомнительной цифры в числе. В качестве значащих цифр могут быть только верные и сомнительные цифры, но если погрешность числа не указана, то все цифры значащие.

Следует применять следующее основное правило записи приближенных чисел (в соответствии со СТ СЭВ 543-77): приближенное число должно быть записано с таким числом значащих цифр, которое гарантирует верность последней значащей цифры числа, например:

1) запись числа 4,6 означает, что верны только цифры целых и десятых (истинное значение числа может быть 4,64; 4,62; 4,56);

2) запись числа 4,60 означает, что верны и сотые доли числа (истинное значение числа может быть 4,604; 4,602; 4,596);

3) запись числа 493 означает, что верны все три цифры; если за последнюю цифру 3 ручаться нельзя, это число должно быть записано так: 4,9·10²;

4) при выражении плотности ртути 13,6 г/см³ в единицах СИ (кг/м³) следует писать 13,6·10³ кг/м³ и нельзя писать 13600 кг/м³, что означало бы верность пяти значащих цифр, в то время как в исходном числе приведены только три верные значащие цифры.

Результаты экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записываются так 4,35·10^-3 и 2,34·10⁵. Подобная запись упрощает вычисления, особенно в случае формул, удобных для логарифмирования.

Округление числа (в соответствии со СТ СЭВ 543-77) представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.

При округлении последняя сохраняемая цифра не изменяется, если:

1) первая отбрасываемая цифра, считая слева направо, меньше 5;

2) первая отбрасываемая цифра, равная 5, получилась в результате предыдущего округления в большую сторону.

При округлении последняя сохраняемая цифра увеличивается на единицу, если

1) первая отбрасываемая цифра больше 5;

2) первая отбрасываемая цифра, считая слева направо, равна 5 (при отсутствии предыдущих округлений или при наличии предыдущего округления в меньшую сторону).

Округление следует выполнять сразу до желаемого числа значащих цифр, а не по этапам, что может привести к ошибкам.

ОБЩАЯ ХАРАКТЕРИСТИКА И КЛАССИФИКАЦИЯ НАУЧНЫХ ЭКСПЕРИМЕНТОВ

Каждый эксперимент представляет собой совокупность трех составных частей: исследуемого явления (процесса, объекта), условий и средств проведения эксперимента. Эксперимент проводится в несколько этапов:

1) предметно-содержательное изучение исследуемого процесса и его математическое описание на основе имеющейся априорной информации, анализ и определение условий и средств проведения эксперимента;

2) создание условий для проведения эксперимента и функционирования исследуемого объекта в желаемом режиме, обеспечивающем наиболее эффективное наблюдение за ним;

3) сбор, регистрация и математическая обработка экспериментальных данных, представление результатов обработки в требуемой форме;

4) содержательный анализ и интерпретация результатов эксперимента;

5) использование результатов эксперимента, например коррекция физической модели явления или объекта, применение модели для прогноза, управления или оптимизации и др.

В зависимости от типа исследуемого объекта (явления) выделяют несколько классов экспериментов: физические, инженерные, медицинские, биологические, экономические, социологические и др. Наиболее глубоко разработаны общие вопросы проведения физических и инженерных экспериментов, в которых исследуются естественные или искусственные физические объекты (устройства) и протекающие в них процессы. При их проведении исследователь может неоднократно повторять измерения физических величин в сходных условиях, задавать желаемые значения входных переменных, изменять их в широких масштабах, фиксировать или устранять влияние тех факторов, зависимость от которых в настоящий момент не исследуется.

Классификацию экспериментов можно провести по следующим признакам:

1) степени близости используемого в эксперименте объекта к объекту, в отношении которого планируется получение новой информации (натурный, стендовый или полигонный, модельный, вычислительный эксперименты);

2) цели проведения – исследование, испытание (контроль), управление (оптимизация, настройка);

3) степени влияния на условия проведения эксперимента (пассивный и активный эксперименты);

4) степени участия человека (эксперименты с использованием автоматических, автоматизированных и неавтоматизированных средств проведения эксперимента).

Результатом эксперимента в широком смысле является теоретическое осмысление экспериментальных данных и установление законов и причинно-следственных связей, позволяющих предсказывать ход интересующих исследователя явлений, выбирать такие условия, при которых удается добиться требуемого или наиболее благоприятного их протекания. В более узком смысле под результатом эксперимента часто понимается математическая модель, устанавливающая формальные функциональные или вероятностные связи между различными переменными, процессами или явлениями.

ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

Исходная информация для построения математической модели исследуемого явления добывается с помощью средств проведения эксперимента, представляющих собой совокупность средств измерений различных типов (измерительных устройств, преобразователей и принадлежностей к ним), каналов передачи информации и вспомогательных устройств для обеспечения условий проведения эксперимента. В зависимости от целей эксперимента иногда различают измерительные информационные (исследование), измерительные контролирующие (контроль, испытание) и измерительные управляющие (управление, оптимизация) системы, которые различаются как составом оборудования, так и сложностью обработки экспериментальных данных. Состав средств измерений в существенной степени определяется математической моделью описываемого объекта.

В связи с возрастанием сложности экспериментальных исследований в состав современных измерительных систем включаются вычислительные средства различных классов (ЭВМ, программируемые микрокалькуляторы). Эти средства выполняют как задачи сбора и математической обработки экспериментальной информации, так и задачи управления ходом эксперимента и автоматизации функционирования измерительной системы. Эффективность применения вычислительных средств при проведении экспериментов проявляется в следующих основных направлениях:

1) сокращение времени подготовки и проведении эксперимента в результате ускорения сбора и обработки информации;

2) повышение точности и достоверности результатов эксперимента на основе использования более сложных и эффективных алгоритмов обработки измерительных сигналов, увеличении объема используемых экспериментальных данных;

3) сокращение числа исследователей и появление возможности создания автоматических систем;

4) усиление контроля за ходом проведения эксперимента и повышение возможностей его оптимизации.

Таким образом, современные средства проведения эксперимента представляют собой, как правило, измерительно-вычислительные системы (ИВС) или комплексы, снабженные развитыми вычислительными средствами. При обосновании структуры и состава ИВС необходимо решить следующие основные задачи:

1) определить состав аппаратной части ИВС (средств измерения, вспомогательного оборудования);

2) выбрать тип ЭВМ, входящей в состав ИВС;

3) установить каналы связи между ЭВМ, устройствами, входящими в аппаратную часть ИВС, и потребителем информации;

4) разработать программное обеспечение ИВС.

2. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА И СТАТИСТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Большинство исследований проводят для установления с помощью эксперимента функциональных или статистических связей между несколькими величинами или для решения экстремальных задач. Классический метод постановки эксперимента предусматривает фиксирование на принятых уровнях всех переменных факторов, кроме одного, значения которого определенным образом изменяют в области его определения. Этот метод составляет основу однофакторного эксперимента (такой эксперимент часто называют пассивным). При однофакторном эксперименте, варьируя один фактор и стабилизируя все прочие на выбранных уровнях, находят зависимость исследуемой величины только от одного фактора. Производя большое число однофакторных экспериментов при изучении многофакторной системы, получают частотные зависимости, представленные многими графиками, имеющими иллюстративный характер. Найденные таким образом частные зависимости невозможно объединить в одну большую. В случае однофакторного (пассивного) эксперимента статистические методы применяют после окончания экспериментов, когда данные уже получены.

Использование однофакторного эксперимента для всестороннего исследования многофакторного процесса требует постановки очень большого числа опытов. Для их выполнения в ряде случаев необходимо значительное время, в течение которого влияние неконтролируемых факторов на результаты опытов может существенно измениться. По этой причине данные большого числа опытов оказываются несопоставимыми. Отсюда следует, что результаты однофакторных экспериментов, полученные при исследовании многофакторных систем, часто малопригодны для практического использования. Кроме того, при решении экстремальных задач данные значительного числа опытов оказываются ненужными, так как получены они для области, далекой от оптимума. Для изучения многофакторных систем наиболее целесообразным является применение статистических методов планирования эксперимента.

Под планированием эксперимента понимают процесс определения числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

Планирование эксперимента – это раздел математической статистики. В нем рассматриваются статистические методы планирования эксперимента. Эти методы позволяют во многих случаях при минимальном числе опытов получать модели многофакторных процессов.

Эффективность использования статистических методов планирования эксперимента при исследовании технологических процессов объясняется тем, что многие важные характеристики этих процессов являются случайными величинами, распределения которых близко следуют нормальному закону.

Характерными особенностями процесса планирования эксперимента являются стремление минимизировать число опытов; одновременное варьирование всех исследуемых факторов по специальным правилам – алгоритмам; применение математического аппарата, формализующего многие действия исследователя; выбор стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.

При планировании эксперимента статистические методы применяются на всех этапах исследования и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в ходе эксперимента, при обработке результатов и после эксперимента, принимая решения о дальнейших действиях. Такой эксперимент называют активным и он предполагает планирование эксперимента.

Основные преимущества активного эксперимента связаны с тем, что он позволяет:

1) минимизировать общее число опытов;

2) выбирать четкие логически обоснованные процедуры, последовательно выполняемые экспериментатором при проведении исследования;

3) использовать математический аппарат, формализующий многие действия экспериментатора;

4) одновременно варьировать всеми переменными и оптимально использовать факторное пространство;

5) организовать эксперимент таким образом, чтобы выполнялись многие исходные предпосылки регрессионного анализа;

6) получать математические модели, имеющие лучшие в некотором смысле свойства по сравнению с моделями, построенными из пассивного эксперимента;

7) рандомизировать условия опытов, т. е. многочисленные мешающие факторы превратить в случайные величины;

8) оценивать элемент неопределенности, связанный с экспериментом, что дает возможность сопоставлять результаты, получаемые разными исследователями.

Чаще всего активный эксперимент ставят для решения одной из двух основных задач. Первую задачу называют экстремальной. Она заключается в отыскании условий процесса, обеспечивающих получение оптимального значения выбранного параметра. Признаком экстремальных задач является требование поиска экстремума некоторой функции (*проиллюстрировать графиком*). Эксперименты, которые ставят для решения задач оптимизации, называют экстремальными.

Вторую задачу называют интерполяционной. Она состоит в построении интерполяционной формулы для предсказания значений изучаемого параметра, зависящего от ряда факторов.

Для решения экстремальной или интерполяционной задачи необходимо иметь математическую модель исследуемого объекта. Модель объекта получают, используя результаты опытов.

При исследовании многофакторного процесса постановка всех возможных опытов для получения математической модели связана с огромной трудоемкостью эксперимента, так как число всех возможных опытов очень велико. Задача планирования эксперимента состоит в установлении минимально необходимого числа опытов и условий их проведения, в выборе методов математической обработки результатов и в принятии решений.

 

ОСНОВНЫЕ ЭТАПЫ И РЕЖИМЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. Содержательный анализ эксперимента, построение априорной вероятностной математической модели источника экспериментальных данных.

2. Составление плана эксперимента, в частности, определение значений независимых переменных, выбор тестовых сигналов, оценка объема наблюдений. Предварительное обоснование и выбор методов и алгоритмов статистической обработки экспериментальных данных.

3. Проведение непосредственно экспериментальных исследований, сбор экспериментальных данных, их регистрация и ввод в ЭВМ.

4. Предварительная статистическая обработка данных, предназначенная, в первую очередь, для проверки выполнения предпосылок, лежащих в основе выбранного статистического метода построения стохастической модели объекта исследований, а при необходимости – для коррекции априорной модели и изменения решения о выборе алгоритма обработки.