Пространственное вращение

Пространственное вращение

Пространственное вращение – один из важнейших видов периоди­ческого движения в стационарных квантовых системах. Напомним, что в классической механике наиболее рациональное описание такого дви­жения достигается при использовании сферической системы координат, с которой мы и начнём свой анализ.

Сферическая система координат

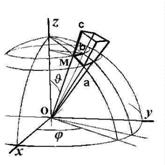
4.3.1.1. Сферическая система координат хорошо известна из географии и астрономии. Положение частица на сфере в этом случае определяется с помощью широты и долготы, которые задаются посредством двух углов и , отсчитываемых относительно фиксированных осей, например, декартовых, как это показано на рис. 4.2. Вводя рас­стояние от центра вращения, переменный радиус r , получаем третью координату, необходимую для описания пространственного вращатель­ного движения

Шаровые координаты:

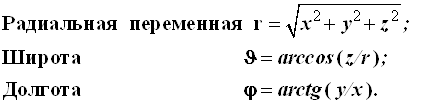
 Декартовы координаты:

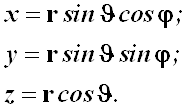(4.28)

Рис. 4.2. Сферическая система координат

При описании переменных данной задачи обязательно следует указать пределы их изменения

 или

 или

 или

4.3.1.2. Вычисление элемента объема в сферической системе ко­ординат проиллюстрируем рис. 4.2. Величина dV понадобится нам в дальнейших расчётах.

 (4.29)

4.3.2. Преобразование оператора Лапласа

4.3.2.1. Лапласиан – основа выражения оператора кинетической энергии и, следовательно, гамильтониана . Поэтому проследим подробно всю схему его преобразования при замене декартовой системы координат на сферическую. С подобной , но более простой процеду­рой мы уже имели дело при рассмотрении плоского ротатора.

4.3.2.2. В теории поля лапласиан является скалярным произве­дением вектор-оператора Гамильтона "набла" самого на себя– скаляр­ным "квадратом" : Поэтому вначале преобразуем оператор "набла"

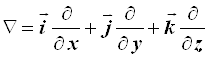. (4.30)

В соответствии с (4.28) x,y,z выражаются как функции сфе­рических координат, поэтому производные, составляющие оператор "набла", предстанут в следующем виде

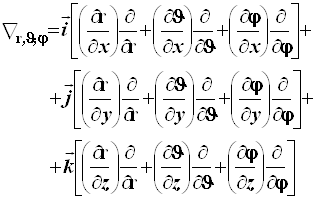(4.31)

4.3.2.3. Наборы частных производных в (4.30) образуют квадрат­ную матрицу коэффициентов, при умножении на которую происходит пе­реход от одного базисного вектор-столбца к другому:

(4.32)

Вычислим все производные, являющиеся элементами квадратной матрицы, дифференцируя выражения (4.28)

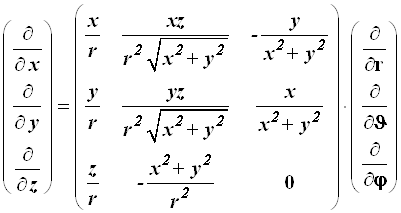или

(4.33)

Напомним, что перемножение матриц подчиняется правилу "строка на столбец". В итоге элементы искомого вектор-столбца предстанут в виде суммы:

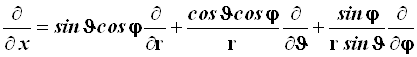(4.34)

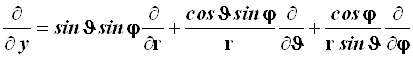(4.35)

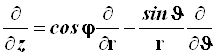(4.36)

4.3.2.4. Следующий этап преобразований – построение оператора Лапласа в переменных .

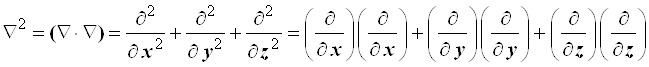(4.37)

Для этого, согласно уравнению (4.35), необходимо перемножить сами на себя выражения операторов однократного дифференцирования по координатам х,у,z через сферические переменные (4.32)–(.4.34) и затем взять сумму этих произведений. При этом следует учитывать, что перемножаются не числа, а операторы, и действие оператора из левой скобки на каждое слагаемое правой выполняется по правилам, аналогичным правилам дифференцирования произведения функций, т.е.

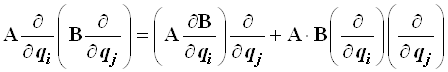(4.38)

4.3.2.5. Ход преобразований продемонстрируем на примере одно­го из слагаемых лапласиана, например при этом, для сохранения упорядоченного характера записи выпишем новые слагаемые, получающиеся в результате дифференцирования, в столбец под каждым преобразуемым выражением. Это в некотором роде изменение привычного математического синтаксиса, цель которого – порядок и наглядность в записи

  

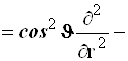
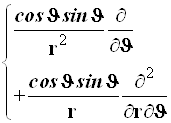
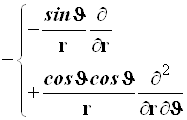
Cуммируя, получаем

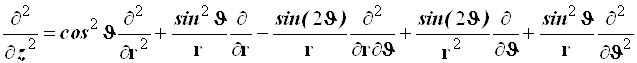. (4.37)