Навигация
Аналогично получаются другие слагаемые лапласиана
6481
знак
2
таблицы
6
изображений
4.3.2.6. Аналогично получаются другие слагаемые лапласиана.
Результаты преобразований представлены в таблице 4.2. В её левом столбце перечислены слагаемые оператора Лапласа в декартовых координатах, а в верхней строчке – все операторы дифференцирования первого и второго порядков по всем сферическим переменным 
, включая перекрёстные, которые возникают в ходе преобразований. На пересечении строк и столбцов указаны коэффициенты перед последними – функции от , которые получаются при преобразовании слагаемых лапласиана, стоящих в левом столбце. Самая нижняя строчка представляет суммы по столбцам. Домножая эти суммы справа на соответствующие операторы верхней строки и суммируя результаты, получаем окончательное искомое выражение оператора Лапласа в сферической системе координат:
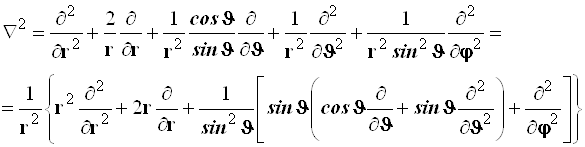(4.38)
4.3.2.7. Сгруппируем некоторые из слагаемых в (4.38) для более компактной записи
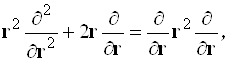(4.39)
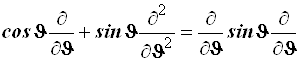, (4.40)
В результате лапласиан приобретает вид
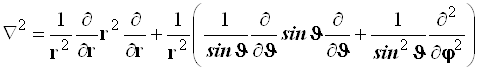(4.41)
Таблица 4.2.
Коэффициенты преобразования оператора Лапласа.
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
| ||
|
|
|
| |||
|
|
|
|
|
| |
|
|
|
|
| ||
|
|
|
| |||
|
|
|
|
| ||
|
|
|
| |||
|
|
|
| 0 | 1 | 0 |
Табл. 4.2.1. Продолжение.
|
|
|
|
| |
|
|
| |||
|
|
| |||
|
|
|
| ||
|
|
| |||
|
|
| |||
|
|
|
|
| |
|
| ||||
|
| ||||
|
| 0 |
| 0 |
|
4.3.2.8. Отдельные фрагменты лапласиана, построенные на разных переменных, удобно обозначить самостоятельными символами. Для краткости переменные отметим в качестве индексов
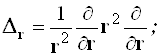(4.42)
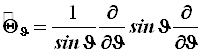(4.43)
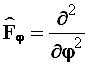. (4.44)
Вся чисто угловая часть лапласиана, заключенная в скобки в формуле (4.41) называется оператором Лежандра 
.
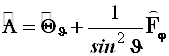(4.45)
В целом же лапласиан оказывается такой комбинацией трёх операторов, которая обеспечивает далее разделение переменных во многих дифференциальных уравнениях, в том числе и в уравнении Шредингера, построенных на его основе:
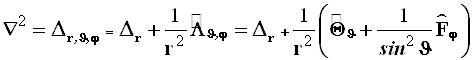(4.46)
4.3.2.9. Напомним, что с оператором 
(4.44) составляющим самую внутреннюю часть конструкции и оператора Лапласа, и оператора Лежандра
мы уже имели дело при рассмотрении одномерного вращения (раздел 3.2.). Были найдены его собственные волновые функции, которые далее войдут в качестве одного из сомножителей 
общих собственных функций этих операторов.
Присутствие радиального слагаемого 
в этом случае заставляет представить оператор кинетической энергии 
в виде суммы
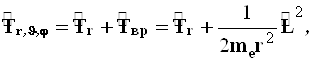(4.50)
4.3.3.3. В силу того, что оператор кинетической энергии частицы отличается от лапласиана только множителем 
(см. уравнение 2.15), домножив на него формулу (4.46), получим
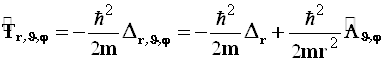(4.51)
Сравнивая формулы (4.50) и (4.51), приходим к фундаментальному соотношению
, (4.52)
т.е. оператор квадрата момента импульса совпадает с оператором Лежандра с точностью до постоянного множителя 
. Заметим, что размерность собственных значений оператора 
совпадает с размерностью постоянной Планка 
.
4.3.3.4. Этот же результат можно получить и последовательными математическими преобразованиями компонент операторов 
и
. Процедура перехода к сферическим координатам для компонент 
аналогична той, что была осуществлена в разделе 3.2.2. при переводе 
к плоской полярной системе координат. Кстати говоря, в сферических координатах имеет тот же самый вид (3.24). Используя уравнения (4.52) и (4.34), читатель сам легко получит выражения
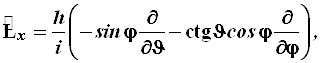(4.53)
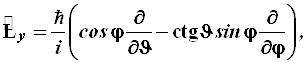(4.54)
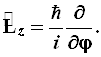(3.24)
Суммируя результаты возведения в квадрат найденных выражений для операторов проекций момента импульса, получаем формулу (4.52), которая в развернутой форме с учетом (4.45) имеет вид
(4.55)
Похожие работы
... вращении частиц в электрон-позитронной системе, известной как атом позитрония. Такое движение называется центральным, а сама задача Кеплеровой. Электрон невозможно зафиксировать на сфере постоянного радиуса – это запрещено принципом неопределенности. При движении электрона как бы образуется пространственное облако. Тем не менее, можно обратиться к аналогии с классической механикой, которая ...
... логический смысл безразмерной постоянной тонкой структуры выражается в том, что она показывает соответствие между континуумом Минковского и квартернионным время-пространством. Я полагаю, что Вольфганг Паули, который настаивал на теоретическом обосновании физического статуса этого загадочного числа 137,0306..., имел в виду нечто подобное. Однако формальных аргументов здесь не достаточно. Мы должны ...
... в пределах 1000 миль от горизонта событий. Динамические модели предсказывали и раньше, что Cygnus XR-1's относится к черной дыре. Газ не может непосредственно падать в нее, как в канаву, но образовывает завихрение в виде сглаженного спирального диска. 7. Пространственно-временные парадоксы. Теории о путешествиях во времени, всегда остаются одними из самых впечатляющих вслед за разработками в ...
... в двадцать пять лет. Многие из этих качеств переносились на женщин, которых они могли любить, бояться или ненавидеть за то, что те имеют такие качества. 5. Модель поведения Разворачивая тему половой дифференциации мышления, я перехожу к структуре, к модели поведения мужчин и женщин. Рассмотрение модели поведения, позволит нам перейти к сущности мужчин и женщин, т. е. к существованию этих, как бы ...
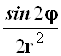
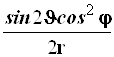
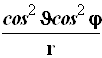
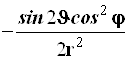
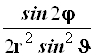
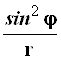
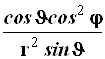
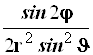
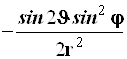
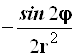
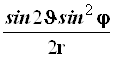
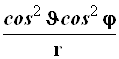
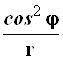
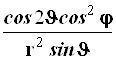
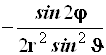
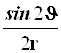
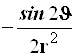
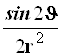
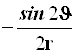
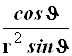
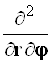
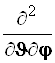
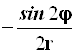
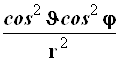
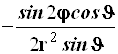
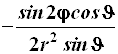
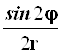
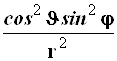
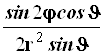
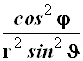
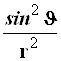
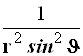
0 комментариев