Навигация
Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
6. Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
Якщо хвилі, поширюючись в пружному середовищі з кінцевою швидкістю, переносять енергію, то вони називаються біжучими. Перенос енергії в хвильовому русі кількісно характеризується вектором густини потоку енергії. Вектор потоку енергії вперше для механічних пружних хвиль був введений російським фізиком Умовим і називається вектором Умова. Напрямок вектора Умова збігається з напрямком переносу енергії, а його модуль дорівнює енергії, яка переноситься хвилею через одиничну площадку, розташовану перпендикулярно до напрямку поширення хвилі, за одиницю часу.
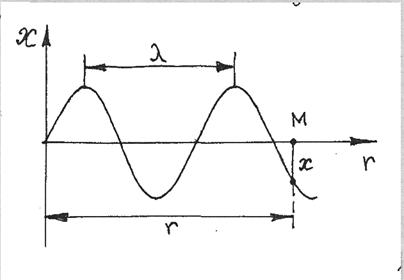
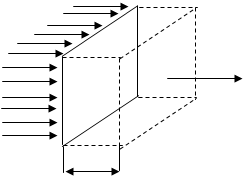
Для одержання рівняння біжучої хвилі ─ залежності зміщення коливної точки пружного середовища від координати і часу ─ розглянемо плоску синусоїдальну хвилю, допустивши, що вісь х збігається з напрямком поширення хвилі (рис. 21). У даному випадку хвильові поверхні, тобто поверхні однакової фази, перпендикулярні до осі х, а тому всі точки пружного середовища на цих поверхнях коливаються однаково. Зміщення будь якої точки пружного середовища від положення рівноваги в цьому випадку залежить лише від координати х і часу t, а його величина буде дорівнювати ![]()
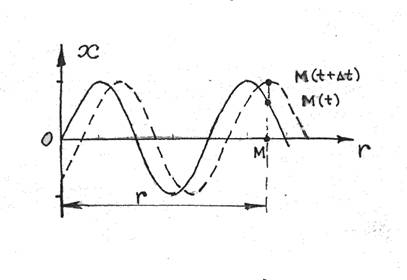
Розглянемо деяку точку В, яка перебуває на відстані х від джерела коливань (рис. 1). Якщо коливання точок пружного середовища, які лежать у площині х = 0, описуються функцією U(0,t) = A cos![]() , то точка В пружного середовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х потрібен час τ =
, то точка В пружного середовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х потрібен час τ = ![]() , де
, де ![]() – швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х, буде мати вигляд
– швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х, буде мати вигляд
![]() (2)
(2)
де А – максимальне зміщення виділеної коливної точки В від положення рівноваги; ω – циклічна частота генератора коливань джерела.
Рівняння (2) є рівняння біжучої хвилі. Якщо плоска хвиля поширюється в протилежному напрямку, то
![]()
В загальному випадку рівняння плоскої синусоїдальної хвилі, яка поширюється без поглинання енергії уздовж позитивного напрямку осі х, має вигляд
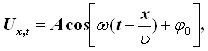 (3)
(3)
де А – амплітуда хвилі; ω – циклічна частота хвилі;![]() – початкова фаза коливань, обумовлена вибором початкових значень х і t; [ω (t - x/υ) + φ0] – фаза плоскої хвилі.
– початкова фаза коливань, обумовлена вибором початкових значень х і t; [ω (t - x/υ) + φ0] – фаза плоскої хвилі.
В рівнянні (3) синусоїдальний характер хвилі характеризують хвильовим числом, яке дорівнює
![]() (4)
(4)
З врахуванням (4) рівняння (3) матиме вигляд
![]() (5)
(5)
Рівняння хвилі, яка поширюється в сторону менших значень осі х, відрізняється від (5) тільки знаком члена kх.
Розглянемо випадок, коли в процесі хвильового руху, фаза коливань не змінюється з часом, тобто
![]() (4.6)
(4.6)
Диференціюємо вираз (6) за часом, одержимо
![]() ,
,
звідки
![]()
Отже, швидкість υ поширення хвилі в рівнянні (6) є не що інше, як швидкість переміщення фази хвилі, а тому її називають фазовою швидкістю.
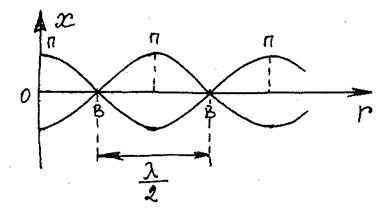
Сферичні хвилі утворюються в однорідному і ізотропному середовищі від точкових джерел коливань. Якщо повторити хід міркувань для плоскої хвилі, можна показати, що рівняння сферичної синусоїдальної хвилі – хвилі, хвильові поверхні якої мають вигляд концентричних сфер, записується так
![]() (7)
(7)
де r – відстань від точкового джерела сферичних хвиль до виділеної точки пружного середовища.
У випадку сферичної хвилі навіть у середовищі, яке не поглинає енергії, амплітуда коливань не залишається постійною, а зменшується з відстанню за законом ![]() Рівняння (7) має місце лише для великих r, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим).
Рівняння (7) має місце лише для великих r, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим).
З рівняння (3) можна одержати, що
![]()
тобто фазова швидкість синусоїдальних хвиль залежить від їхньої частоти. Це явище називають дисперсією хвиль, а середовище, у якому спостерігається дисперсія хвиль, називається дисперсним середовищем.
Похожие работы
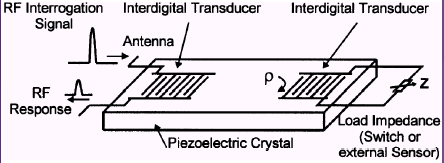
... чено раніше, якщо вибрати правильний напрямок поширення хвилі, можна створити бездротової датчик температури. Середовище поширення міняється разом з температурою, впливаючи на дані на виході. Нижче наведені деякі найбільш загальні способи застосування датчиків акустичних хвиль. Термодатчик будується на термозалежності швидкості поверхневих хвиль, яка визначається напрямком і типом кристалічного ...
... є поширення гіперзвуку в п’єзоелектричних матеріалах (напр., кристалах CdS), де пружні хвилі супроводжуються електромагнітними хвилями, і навпаки. У таких кристалах згасання і дисперсія гіперзвуку відбуваються в результаті його взаємодії з просторовими зарядами, зумовленими внутрішніми електричними полями. У цьому випадку діє також механізм електрон-фононної взаємодії, який обумовлений електричною ...
... – 2007. Міжнародна наукова конференція. Матеріали конференції. – Дніпропетровськ, Дніпродзержинськ. – 2007. – С.105. АНОТАЦІЯ Головко К.Г. Осесиметричні коливання дискретно підкріплених оболонкових елементів конструкцій на пружній основі при імпульсних навантаженнях. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за фахом 01.02.04 - механіка деформівного твердого ...
... різних точок середовища в один і той же момент часу, а на графіку гармонічного коливного руху зображено положення однієї і тієї ж точки, що коливається, в різні моменти часу. 3.Енергія хвилі. Вектор Умова Процес поширення хвилі в якому-небудь напрямі в середовищі супроводжується переносом енергії коливань в цьому напрямі. Розглянемо плоску хвилю. Нехай S- це частина її фронту в момент часу ...
0 комментариев