Навигация
Одномірне хвильове рівняння. Швидкість поширення хвиль
7. Одномірне хвильове рівняння. Швидкість поширення хвиль
Рівняння довільної хвилі є розв'язком рівняння, яке називається хвильовим.
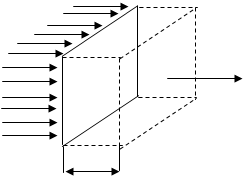
Для виведення цього рівняння скористаємось рівняння плоскої хвилі, яка поширюється в напрямку осі х. Розглянемо ділянку пружного середовища, яке характеризується модулем пружності Е (рис. 2). З рисунка видно, що виділений елемент має переріз S і довжину Δх. Під дією зовнішньої сили F виділена ділянка пружного середовища деформується на величину ΔU.
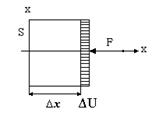
Рис. 2
Оскільки середовище є пружним, то для виділеної ділянки можна застосувати закон Гука
![]() (8)
(8)
де Е ─ модуль Юнга; ![]() ─ відносна деформація; F ─ зовнішня сила; S ─ площа виділеної ділянки пружного середовища в напрямі осі х.
─ відносна деформація; F ─ зовнішня сила; S ─ площа виділеної ділянки пружного середовища в напрямі осі х.
В граничному випадку при ![]() , рівняння (8) запишеться так
, рівняння (8) запишеться так
![]() (9)
(9)
Якщо збуджувати поздовжню хвилю в деякому пружному середовищі, яким є наприклад стержень перерізом S з модулем Юнга Е, то на виділену ділянку будуть діяти дві сили (рис.3). Запишемо для цієї ділянки другий закон Ньютона
![]() (10)
(10)
Сили в рівнянні (10) є пружними силами, а тому відповідно до рівняння (9) запишуться так
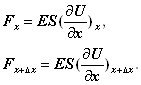
![]() (11)
(11)
Якщо підставити ці сили (11) в другий закон Ньютона (10), то після деяких перетворень одержимо
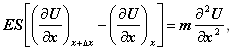 (12)
(12)
де m ─ маса виділеної ділянки пружного середовища.
Масу виділеної ділянки пружного середовища можна виразити через об’єм і густину речовини стержня так
m = ρSΔx. (13)
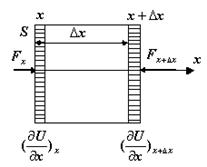
Рис.3
З урахуванням значення маси (13) і нескладних перетворень рівняння (12) запишеться так
![]() (14)
(14)
Розглянувши граничний випадок при якому![]() , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням
, з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням
![]() (15)
(15)
Рівняння (15) є лінійним диференціальним рівнянням другого порядку в частинних змінних. Розв’язком такого рівняння є уже відоме рівняння плоскої хвилі
![]() (16)
(16)
Знайдемо другі частинні похідні за часом t і координатою х від рівняння (16)
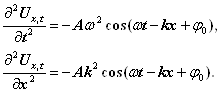 (17)
(17)
Після підстановки похідних (17) в рівняння (15) та необхідних скорочень одержимо
![]() (18)
(18)
Але оскільки ![]() , то хвильове рівняння (15) буде мати інший вигляд
, то хвильове рівняння (15) буде мати інший вигляд
![]() (19)
(19)
Таким чином швидкість поширення механічних хвиль у пружному середовищі залежить від пружних властивостей цього середовища і його густини
![]() (20)
(20)
Оскільки модуль Юнга характеризує стиснення або розтягування пружного середовища, то одержана швидкість (20) є фазовою швидкістю лише поздовжніх хвиль.
Фазова швидкість поперечних хвиль, які можуть існувати лише в твердому пружному середовищі, визначають заміною модуля Юнга в (20) на модуль зсуву G
![]() (21)
(21)
Розрахунки показують, що в твердому середовищі модуль Юнга E майже на порядок перевищує модуль зсуву G, тому фазова швидкість поздовжньої хвилі тут більша за швидкість поперечної хвилі, тобто
![]() (22)
(22)
Важливо відмітити, що для механічних хвиль, які мають велику довжину λ рівняння (15) і (19) будуть нелінійними.
Якщо механічна хвиля поширюється в однорідному ізотропному середовищі, то хвильове рівнянням буде мати вигляд:
![]() (23)
(23)
Для механічних хвиль властивий принцип суперпозиції. Це означає, що при накладанні механічних хвиль відсутнє їх спотворення.
8. Енергія пружних хвиль. Потік і густина потоку енергії хвиль
Нехай в деякому пружному середовищі в напрямі осі х поширюється плоска поздовжня хвиля
![]() . (24)
. (24)
Виділимо в цьому середовищі елементарний об’єм ΔV, настільки малий, щоб швидкість хвилі ![]() і швидкість деформації
і швидкість деформації ![]() у всіх його точках були однакові.
у всіх його точках були однакові.
Повну механічну енергію, локалізовану у виділеному об’ємі розраховують за формулою
![]()
де ![]() - кінетична енергія виділеного об’єму;
- кінетична енергія виділеного об’єму; ![]() - потенціальна енергія пружної деформації цього об’єму.
- потенціальна енергія пружної деформації цього об’єму.
Кінетичну енергію, яку має виділений об’єм пружного середовища знаходимо за формулою
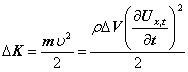 , (25)
, (25)
де ρ - густина середовища виділеного об’єму.
Першу похідну за часом від (24) підставимо в (25), одержимо
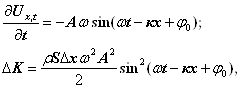 (26)
(26)
де ![]() ─ хвильове число.
─ хвильове число.
У відповідності з рис. 4 потенціальну енергію пружної деформації виділеного об’єму знаходимо так:
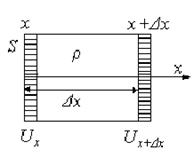
Рис. 4
![]() (27)
(27)
де k – коефіцієнт пружності середовища, який відповідно до закону Гука (8) дорівнює ![]() ;
; ![]() ─ величина деформації виділеного об’єму пружного середовища.
─ величина деформації виділеного об’єму пружного середовища.
З урахуванням цих позначень (27) матиме вигляд
![]() . (28)
. (28)
Помножимо й поділимо (28) на Δх2, одержимо
![]() (29)
(29)
В граничному випадку при Δх=0 одержуємо
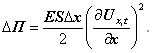 (30)
(30)
Підставимо у формулу (30) значення модуля Юнга ![]() , і швидкість деформації
, і швидкість деформації ![]() , одержимо
, одержимо
![]() (31)
(31)
Повну енергію, локалізовану у виділеному об’ємі пружного середо-вища, одержимо при додаванні кінетичної енергії (26) і потенціальної енергії (31)
![]() (32)
(32)
Якщо врахувати, що середнє значення квадрата синуса за час в один період дорівнює ![]() , то одержимо середнє значення повної енергії буде дорівнювати
, то одержимо середнє значення повної енергії буде дорівнювати
![]() (33)
(33)
де ΔV=SΔx ─ елементарних об’єм пружного середовища.
Середнє значення густини енергії легко одержати, якщо (33) поділити її на величину виділеного об’єму пружного середовища
![]() . (34)
. (34)
Нехай через площадку S (рис.4), яка є перпендикулярною до напрямку поширення хвилі, за час Δt переноситься енергія ΔW. Тоді вектор густини енергії буде дорівнювати
![]() , (35)
, (35)
де ![]() ─ вектор густини потоку енергії;
─ вектор густини потоку енергії; ![]() ─ середня густина перенесеної хвилями енергії;
─ середня густина перенесеної хвилями енергії; ![]() ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії.
─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії.
Вектор потоку енергії ![]() вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова.
вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова.
Похожие работы
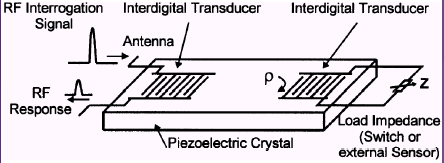
... чено раніше, якщо вибрати правильний напрямок поширення хвилі, можна створити бездротової датчик температури. Середовище поширення міняється разом з температурою, впливаючи на дані на виході. Нижче наведені деякі найбільш загальні способи застосування датчиків акустичних хвиль. Термодатчик будується на термозалежності швидкості поверхневих хвиль, яка визначається напрямком і типом кристалічного ...
... є поширення гіперзвуку в п’єзоелектричних матеріалах (напр., кристалах CdS), де пружні хвилі супроводжуються електромагнітними хвилями, і навпаки. У таких кристалах згасання і дисперсія гіперзвуку відбуваються в результаті його взаємодії з просторовими зарядами, зумовленими внутрішніми електричними полями. У цьому випадку діє також механізм електрон-фононної взаємодії, який обумовлений електричною ...
... – 2007. Міжнародна наукова конференція. Матеріали конференції. – Дніпропетровськ, Дніпродзержинськ. – 2007. – С.105. АНОТАЦІЯ Головко К.Г. Осесиметричні коливання дискретно підкріплених оболонкових елементів конструкцій на пружній основі при імпульсних навантаженнях. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за фахом 01.02.04 - механіка деформівного твердого ...
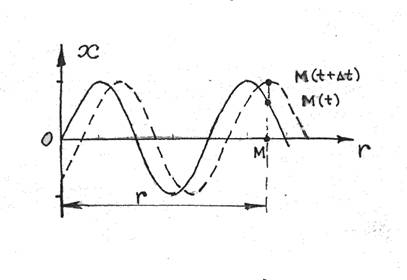
... різних точок середовища в один і той же момент часу, а на графіку гармонічного коливного руху зображено положення однієї і тієї ж точки, що коливається, в різні моменти часу. 3.Енергія хвилі. Вектор Умова Процес поширення хвилі в якому-небудь напрямі в середовищі супроводжується переносом енергії коливань в цьому напрямі. Розглянемо плоску хвилю. Нехай S- це частина її фронту в момент часу ...
0 комментариев