Навигация
Вычисляем фактические контактные напряжения
13084
знака
0
таблиц
4
изображения
2.9.4 Вычисляем фактические контактные напряжения
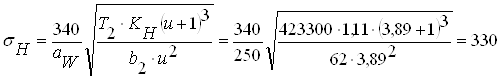МПа ;
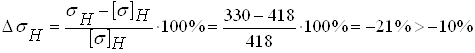
Принимаем b2 = 45 мм, тогда
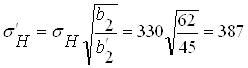МПа
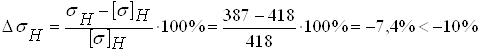
Принимаем b1 = 50 мм и уточняем Ψbd= b2/d1 = 45/100 = 0,45 .
2.9.5 Проверяем зубья на выносливость по напряжениям изгиба
Уточняем коэффициент нагрузки:
КF = КFβ· КFυ = 1,08 · 1,45 = 1,57 ;
Принимаем:
КFβ = 1,08[2]
КFυ = 1,45[2]
YF – коэффициент, учитывающий форму зуба;
YF1 = 3,7[2]
YF2 = 3,6[2]
Вычисляем напряжения изгиба:
;
МПа < [σ]F1 ;
МПа < [σ]F2 ;
2.9.6 Выполняем проверочный расчет на статическую прочность от действия перегрузок.
;
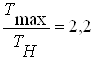Определяем коэффициент перегрузки:
;
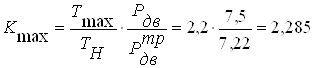Находим контактное напряжение:
σHmax = σH · 
= 387 · 
= 585 МПа ;
Находим изгибные напряжения:
σFmax1= σF1· Кmax = 105 · 2,285 = 240 МПа ;
σFmax2= σF2· Кmax = 114 · 2,285 = 260 МПа .
Для термообработки улучшение и нормализация:
[σ]Hmax= 2,8 · σТ[3]
[σ]Fmax= 0,8 · σТ
где σТ – предел текучести материала.
Для колеса σТ = 340 МПа ;
[σ]H2max= 2,8 · 340 = 952 МПа > σHmax;
[σ]F2max= 0,8 · 340 = 272 МПа > σF2max;
Условие статической прочности выполняется.
3. Расчёт зубчатой передачи быстроходной ступени редуктора
3.1 Выбор материалов
Принимаем для изготовления зубчатых колес быстроходной ступени редуктора тот же материал и термообработку, что и для тихоходной ступени. Такой выбор уменьшает номенклатуру материалов.
Шестерня – сталь 45, термообработка – улучшение;
(192…240) НВ,НВср=Н1=215 ;
Н1≥Н2 + (10…15)НВ;[3]
Колесо – сталь 45, термообработка – нормализация;
(170…217)НВ,НВср=Н2=195.
3.2 Определяем базовое число циклов перемены напряжений.
а) по контактным напряжениям:
NН0 = 30 · НВ2,4;
для шестерни N01 = 
;
для колеса N02 = 
;
б) по напряжениям изгиба:
NF0 = 4 · 106.
3.3 Определяем фактическое число циклов перемены напряжений.
а) по контактным напряжениям:
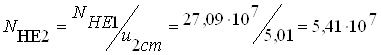
б) по напряжениям изгиба:
где m – показатель степени кривой усталости. При твёрдости меньше 350НВ m = 6.
Тогда,
;
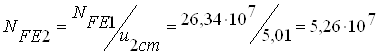3.4 Вычисляем коэффициент долговечности
а) по контактным напряжениям.
;
Для шестерни:
;
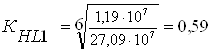Так как NНЕ1> NН01, то принимаем KHL1=1;
Для колеса:
;
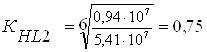Так как NНЕ2> NН02, то принимаем KHL2=1.
б) по напряжениям изгиба.
Так как NFE1 > 4∙106 и NFE2 > 4∙106, то принимаем KFL1=1 и KFL2=1.
3.5 Вычисляем базовое значение предела выносливости:
а) для контактных напряжений
Для термообработки улучшения
σ0нlimb=2·HB+70 [2]
Для шестерни:
σ0нlimb1 = 2·215 + 70 = 500 МПа.
Для колеса:
σ0нlimb2 = 2·195 + 70 = 460 МПа.
б) для напряжений изгиба
Для термообработки улучшение и нормализация:
σ0Flimb= 1,8 НВ;[2]
σ0Flimb1= 1,8 · 215 = 387 МПа;
σ0Flimb2= 1,8 · 195 = 351 МПа.
3.6 Определяем допускаемые контактные напряжения:
;
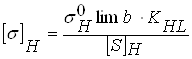- коэффициент запаса.
При термообработке нормализация и улучшение принимаем 
[2]
МПа;
МПа;
Для шевронных передач, согласно рекомендации книги [2]
МПа ;
[2]
МПа > 393 МПа ;
Так как 
, то принимаем 
МПа .
3.7 Определяем допускаемые напряжения изгиба:
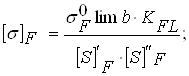
где 
- коэффициент, зависящий от вероятности безотказной работы. Принимаем = 1,75 [2]
- коэффициент, зависящий от способа изготовления заготовки, Для проката = 1,15[2]
МПа;
МПа.
3.8 Проектный расчет цилиндрической прямозубой передачи.
3.8.1 Определяем межосевое расстояние из условия обеспечения контактной прочности зуба.
;
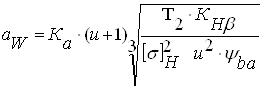Предварительно принимаем КНβ = 1,1[2]
Ψba-ширина зубчатого венца;
Принимаем для прямозубой передачи Ψba= 0,4 и Ка = 43 [2]
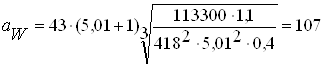мм;
Принимаем ближайшее стандартное значение аW ГОСТ=125 мм [2]
3.8.2 Определяем модуль зацепления:
mn=(0,01…0,02)·аW=(0,01…0,02)·125=1,25…2,5 мм
принимаем mn=2 мм [2]
3.8.3 Определяем основные параметры зубчатых колес:
а) назначаем угол наклона зубьев
β = 30º[2]
б) определяем значение торцевого модуля
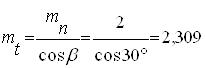мм ;
в) суммарное число зубьев:
Z∑=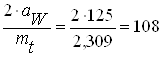
г) уточняем значение mt и β:
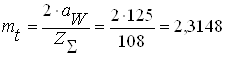мм ;
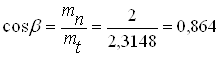
βº = 30,23066º
д) число зубьев шестерни:
Z1= Z∑/(u+1)=108/(5,01+1)=18;
число зубьев колеса:
Z2= Z∑ – Z1 =108 – 18 = 90;
Проверка: аW= (Z1 + Z2) · mt /2 ;
125 = (18 + 90) · 2,3148/2 ;
125 =125 ;
е) диаметры делительных окружностей
d = mt· z;
d1 = 2,3148 · 18 = 41,666 мм;
d2 = 2,3148 · 90 = 208,332 мм;
ж) диаметры окружностей вершин:
da1 = d1 + 2·mn = 41,666 + 2·2 = 45,666 мм;
da2 = d2 + 2·mn = 208,332 + 2·2 = 212,332 мм;
з) диаметры окружностей впадин:
df1 = d1 – 2,5·mn= 41,666 – 2,5·2 = 36,666 мм;
df2 = d2 – 2,5·mn= 208,332 – 2,5·2 = 203,332 мм;
и) ширина колеса и шестерни:
b2 = Ψba· aW= 0,4 · 125 = 50 мм;
b1 = b2 + 4…8 = 50 + 4…8 = 54…58 мм;
Принимаем b1 = 55 мм.
3.9 Проверочный расчет шевронной зубчатой передачи.
3.9.1 Уточняем коэффициент нагрузки:
Для отношения Ψbd= b2/d1 = 50/41,666 = 1,2 , при несимметричном расположении колес относительно опор, КНβ = 1,15[2]
3.9.2 Определение окружной скорости колес и степени точности передачи:
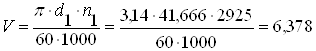м/с;
Принимаем 8-ю степень точности по ГОСТ 1643-81[2]
3.9.3 Определяем коэффициент нагрузки:
KH=KHβ·KHα·KHV= 1,15·1,13·1,01 = 1,31 ;
где KHα- коэффициент неравномерности нагрузки между зубьями;
KHα=1,13 [2]
KHV- коэффициент динамической нагрузки,
KHV=1,01 [2]
3.9.4 Вычисляем фактические контактные напряжения
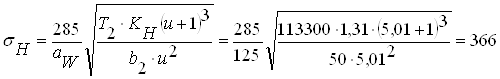МПа ;
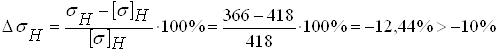
Принимаем b2 = 45 мм, тогда
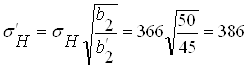МПа
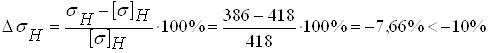
Принимаем b1 = 50 мм и уточняем Ψbd= b2/d1 = 45/41,666 = 1,08 .
3.9.5 Проверяем зубья на выносливость по напряжениям изгиба
Уточняем коэффициент нагрузки:
КF = КFβ· КFυ = 1,26 · 1,3 = 1,64 ;
Принимаем:
КFβ = 1,26[2]
КFυ = 1,3 [2]
Вычисляем коэффициент торцового перекрытия εα :
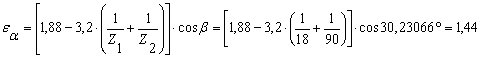
Определяем коэффициент, учитывающий многопарность зацепления
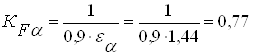
Определяем коэффициент, учитывающий наклон контактной линии:
;
Определяем эквивалентное число зубьев:
;
;
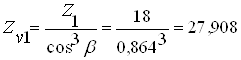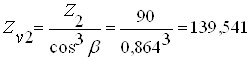YF – коэффициент, учитывающий форму зуба;
YF1 = 3,85[2]
YF2 = 3,6[2]
Вычисляем напряжения изгиба:
;
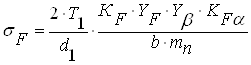МПа < [σ]F1 ;
МПа < [σ]F2 ;
3.9.6 Выполняем проверочный расчет на статическую прочность от действия перегрузок
;
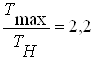Определяем коэффициент перегрузки:
;
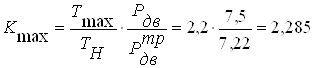Находим контактное напряжение:
σHmax = σH · = 386 · = 583 МПа ;
Находим изгибные напряжения:
σFmax1= σF1· Кmax = 42 · 2,285 = 96 МПа ;
σFmax2= σF2· Кmax = 44 · 2,285 = 101 МПа .
Для термообработки улучшение и нормализация:
[σ]Hmax= 2,8 · σТ[3]
[σ]Fmax= 0,8 · σТ
где σТ – предел текучести материала.
Для колеса σТ = 340 МПа ;
[σ]H2max= 2,8 · 340 = 952 МПа > σHmax;
[σ]F2max= 0,8 · 340 = 272 МПа > σF2max;
Условие статической прочности выполняется
Похожие работы
... и отдельных элементов привода [Л1] (табл. 1.2.1). Для нашего привода (рис.1): Рисунок 1 – Схема привода: 1 – электродвигатель, 2 – ременная передача, 3 – редуктор конический одноступенчатый, 4 – цепная передача. Расчетная мощность электродвигателя, кВт: ; (1.2) На основании рекомендуемых min и max величин передаточных чисел u для ...
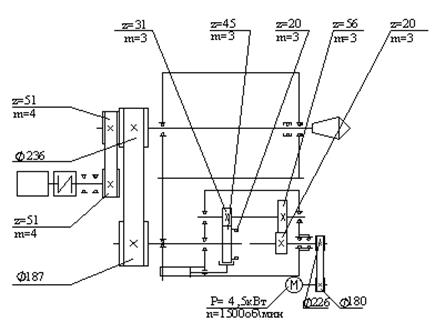
... двигателя и добиваемся его реализации путем изменения числа зубьев в приводе, сохраняя при этом общее число зубьев в сумме. На рисунке 1 приведена принципиальная кинематическая схема привода главного движения станка с учетом индивидуального задания, согласно которому общее передаточное отношение . Рисунок 1 – Кинематическая схема привода 1.1.2 Выбор двигателя Для выбора двигателя ...
ский расчет привода главного движения 3.1 Определение предельных чисел оборотов шпинделя 3.2 Определение числа ступеней АКС 3.3 Определение передаточных отношений 3.4 Расчет числа зубьев передач 4 Расчет поликлиноременной передачи 5 Выбор материала для изготовления зубчатых передач АКС 6 Расчет закрытой зубчатой передачи 7 Проверочный расчет зубчатых передач 8 Расчет валов АКС. 9 Расчет ...
... w и Т заносятся в таблицу 3.1. Примечание. Для одноступенчатого редуктора крутящий момент определяется по формуле , [Н·м]; , [Н·м]; [Н·м]; , [Н·м]. [Н·м]. Расчет клиноременной передачи Расчет клиноременной передачи проводим исходя из ранее рассчитанной мощности электродвигателя, Рэд и принятого передаточного отношения клиноременной передачи iр.п.=2. Определение сечения ремня ...
0 комментариев