Навигация
Расчёт сложных цепей переменного тока символическим методом
3 Расчёт сложных цепей переменного тока символическим методом
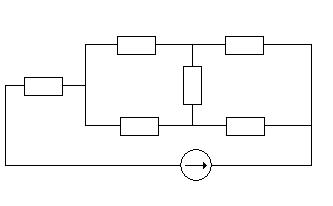
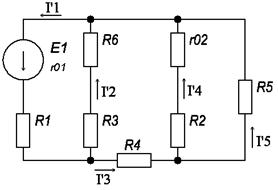
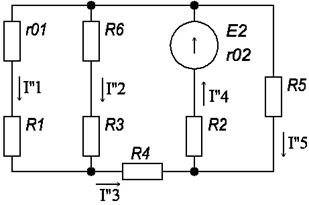
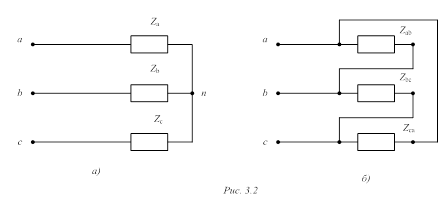
Электрическая схема цепи и комплексная схема замещения представлены на рисунке 5а и б соответственно.
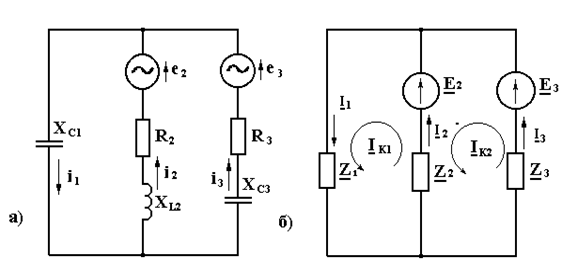
Рисунок 5
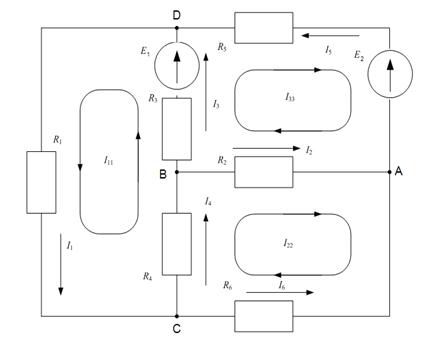
Намечаем в независимых контурах заданной цепи, как показано на рисунке 5б, контурные токи IK1 и IK2 – некоторые расчётные комплексные величины, которые одинаковы для всех ветвей выбранных контуров. Направления контурных токов принимаются произвольно. Для определения контурных токов составляем два уравнения по второму закону Кирхгофа:
![]() IK1*(Z1 + Z2) – IK2*Z2 = E2
IK1*(Z1 + Z2) – IK2*Z2 = E2
- IK1*Z2+IK2*(Z2+Z3)= E3 - E2
Подставляем данные в систему:
IK1*(- j65+14+j56) – IK2*(14+j56) = 230
-IK1*(14+j56) +IK2 *(14+j56+56 – j23) = j240-230
IK1*(14-j9) – IK2*(14+j56) = 230
-IK1*(14+j56) + IK2*(70+j33) = -230+ j240
Решаем систему с помощью определителей. Определитель системы:
 =1277-j168+2940– j1568=4217-j1736
=1277-j168+2940– j1568=4217-j1736
Частные определители :
![]() =
= 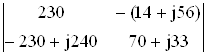 = 16100+j7590–16660-j9520= -560–j1930.
= 16100+j7590–16660-j9520= -560–j1930.
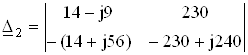 =-1060+j5430+3220+j12880 = 2160+j18310
=-1060+j5430+3220+j12880 = 2160+j18310
Определяем контурные токи:
IK1 = ![]() =
= 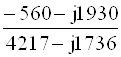 = 0.0476-j0.438 A.
= 0.0476-j0.438 A.
IK2 = ![]() =
= 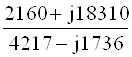 = - 1.09+ j3.89 A.
= - 1.09+ j3.89 A.
Действительные токи в ветвях цепи определяем как результат наложения контурных токов:
I1 = IK1 = 0.0476 – j0.438 = 0.441![]() A
A
I2 = IK1-IK2 = 0.0476.- j0.438+1.09- j3.89 = 1.14 – j4.33 = 4.48![]() A
A
I3 = IK2 = -1.09 + j3.89 = 4.04![]() A.
A.
Составляем уравнение баланса мощностей в заданной электрической цепи. Определяем комплексные мощности источников:
SE2 = E2*![]() =230(1.14+j4.33) = 262+j996=1030
=230(1.14+j4.33) = 262+j996=1030![]() B*A
B*A
SE23= E3*![]() = j240*(-1.09 – j3.89) = 912 – j262 = 949
= j240*(-1.09 – j3.89) = 912 – j262 = 949![]() B*A
B*A
Определяем комплексные мощности приёмников электрической энергии:
S1 = I12*Z1 =0.4412*( – j65) = – j12.6 =12.6![]() B*A
B*A
S2 = I22*Z2 = 4.482*(14+j56) = 281+j1124=1159![]() B*A
B*A
S3 = I32*Z3 = 4.042*(56 – j23) = 914– j375 =988![]() B*A.
B*A.
Уравнение баланса комплексных мощностей!
SЕ1 + SE2 = S1 + S2 + S3;
262+j996+912-j262 = – j12.6+281+j1124+914– j375
1174+ j734 @ 1182+ j749; 1385![]() @ 1400
@ 1400 ![]()
Относительная и угловая погрешности незначительны.
Для построения векторной диаграммы задаёмся масштабами токов MI = 0.25 А/см и ЭДС ME = 50 В/см. Векторная диаграмма в комплексной плоскости построена на рисунке 6.
4 Расчёт трёхфазной цепи при соединении приемника в звезду
Схема заданной цепи изображена на рисунке 7.
Определяем систему фазных напряжений генератора. Фазное напряжение:
UФ = Uл/![]() = 380/1,73=220 В.
= 380/1,73=220 В.
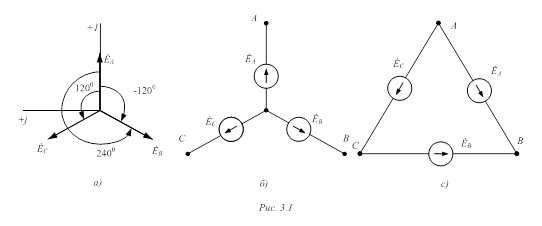
Комплексные фазные напряжения генератора:
UA = UФ = 220 B
UB = UAe-j120 = 220e-j120 = –110 – j191 B
UC = UAej120 = 220ej120 = –110 + j191 B
Определяем полные проводимости фаз приёмника:
YA = 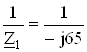 = j0,01538 См.
= j0,01538 См.
YB =  = 0.0042-j0.0168 См.
= 0.0042-j0.0168 См.
YC = 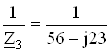 = 0.0153+j0.00628Cм.
= 0.0153+j0.00628Cм.
YN=![]() =
=![]() = j0.03125 См.
= j0.03125 См.
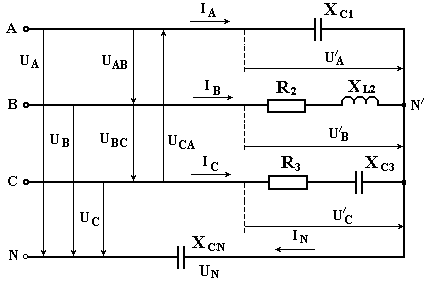
Рисунок 7
Узловым напряжением является в данном случае напряжение смещения нейтрали, которое определяется по формуле:
UN=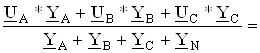
![]()
![]()
= (j3.38-3.67+j1.05-2.88+j2.23)/(0.05075+j0.00486) = (-6.55+j6.66)/(0.0195+j0.03611)= 67+j218 = 228![]() B.
B.
Определяем фазные напряжения на нагрузке:
UA/ = UA – UN = 220- (67+j218) = 153-j218 = 266![]() B.
B.
UB/ = UB – UN = (–110-j191) - (67+j218) = -177-j409 =446![]() B.
B.
UC/ = UC–UN=(–110+j191) - (67+j218) = -177 – j27 = 179![]() B.
B.
Определяем токи в фазах нагрузки:
IA = UA/*YA = (153-j218)*(j0.01538) = 3.35+j2.35 = 4.1![]() A.
A.
IB = UB/*YB = (-177-j409)*(0.0042-j0.0168) = -7.61+j1.26 =7.72![]() A.
A.
IC=UC/*YC= (-177 – j27)*(0.0153+j0.00628)=- 2,53–j1,52= 2,96![]() A.
A.
IN= UN*YN = (67+j218)*j0.03125 = - 6,8 + j2,09 = 7,12*![]()
Проверяем правильность определения токов по первому закону Кирхгофа для точки N’:
IA + IB + IC =IN
3.35+j2.35 -7.61+j1.26 - 2,53 – j1,52 @ - 6,8 + j2,09;
- 6,79+j2.09 @ - 6,8 + j2,09.
Определяем комплексные мощности фаз и всей цепи:
SA = IA2 * Z1 = 4,12*(-j65) = -j1092=1092![]() B*A.
B*A.
SB = IB2 * Z2 = 7,722*(14+j56) = 834+j3338 =3440![]() B*A
B*A
SC = IC2 * Z3 = 2,962*(56-j23) = 491 – j 202 = 530![]() B*A.
B*A.
S= SA + SB + SC = -j1092+ 834+j3338+ 491 – j 202 = 1325+j2044 =
= 2436![]() B*A.
B*A.
Для построения векторной диаграммы задаёмся масштабами токов MI = 1 А/см и напряжений MU = 40 B/см. Векторная диаграмма на комплексной плоскости построена на рисунке 8.
5 Расчёт трёхфазной цепи при соединении приёмника в треугольникСхема заданной цепи изображена на рисунке 9
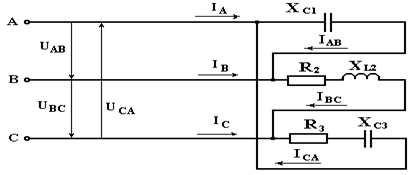
Рисунок 9.
В данном случае линейные напряжения генератора являются фазными
напряжениями нагрузки:
UAB = UЛ = 380 В.
UBC = 380![]() = -190-j329 B.
= -190-j329 B.
UCA = 380![]() = -190+j329 B.
= -190+j329 B.
Определяем систему фазных токов нагрузки:
IAB =![]() =
= ![]() = j5,85 = 5,85
= j5,85 = 5,85![]() A
A
IBC = ![]() =
= 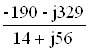 = -6,32+j1,81 = 6,58
= -6,32+j1,81 = 6,58![]() A
A![]()
ICA = ![]() =
= 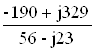 = -4,96+j3,83 = 6,27
= -4,96+j3,83 = 6,27![]() A
A
Систему линейных токов определяем из соотношений:
IA = IAB – ICA = j5,85+4,96-j3,83 = 4,96+j2,02 = 5,36![]() A
A
IB = IBC – IAB = -6,32+j1,81-j5,85 = -6,32-j4,04 = 7,5![]() A
A
IC = ICA – IBC = -4,96+j3,83+6,32-j1,81 = 1,36+j1,92 =2,35![]() A
A
Определяем мощности фаз приемника:
SAB=IAB2*Z1 = 5,852*(-j65) = -j2224 = 2224![]() B*A.
B*A.
SBC = IBC2*Z2 = 6,582*(14+j56) = 606+j2425 = 2499![]() B*A.
B*A.
SCA = ICA2*Z3 = 6,272*(56 – j23) =2201– j904 = 2380*![]() B*A.
B*A.
Определяем мощность трехфазной нагрузки:
SAB+SBC +SCA = -j2224+606+j2425+2201– j904 =2807 – j703 =
= 2894![]() B*A.
B*A. ![]()
Для построения векторной диаграммы задаёмся масштабами токов MI =1 A/см и напряжений MU = 50A/см. Векторная диаграмма построена на рисунке 10.
6 Расчёт неразветвлённой цепи с несинусоидальными напряжениями и токами
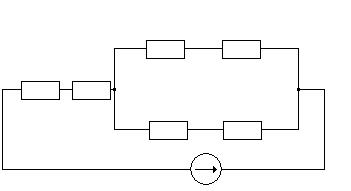
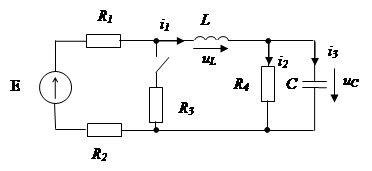
Составляем схему заданной цепи, подключая последовательно соединённые приёмники к источнику несинусоидального напряжения, под действием которого в цепи возникает ток с мгновенным значением
i=7Sin(wt+130)+1,2Sin(2wt-860)+0,4Sin3wt A, который на схеме замещения представляем как последовательно соединённые три источника переменного напряжения u1, u2 и u3 c разными частотами (рисунок 11)
Величины сопротивлений заданы для частоты первой гармоники:
XC11 = 18 Ом, R2 = 23 Ом, XL21 = 14 Ом, R3 = 12 Ом, XC31 = 62 Ом. Поскольку напряжения источников имеют разные частоты, то и реактивные сопротивления для них будут иметь разные величины. Активные сопротивления считаем от частоты не зависящими. Поэтому расчёт ведём методом наложения, то есть отдельно для каждой гармоники.
. 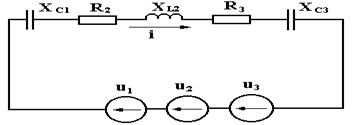
Рисунок 11.
Первая гармоника
Определяем активное и реактивное сопротивления всей цепи:
R = R2 + R3 = 14+56 = 70 Ом. X1 = -XC11+ XL21- XC31 = - 65+56–23 =
= -32 Ом.
Полное сопротивление цепи:
Z1 = ![]() =
= ![]() = 76,7 Ом.
= 76,7 Ом.
Амплитудные значения напряжения и тока:
Im1 = 7 A, Um1 = Im1*Z1= 7*76.7 =537 B.
Действующие значения напряжения и тока:
U1 = Um1 / ![]() = 537 / 1,41 = 381 B.
= 537 / 1,41 = 381 B.
I1 = Im1 / ![]() = 7 / 1,41 = 4.96 A.
= 7 / 1,41 = 4.96 A.
Угол сдвига фаз между напряжением и током определяем по синусу:
Sinφ1 = X1/Z1 = -32/76.7 = - 0.4172. j1= - 24.66°, Cosφ1=0.9088.
Активная и реактивная мощности первой гармоники:
P1 = I12 * R = 4.962 * 70 =1722 Вт.
Начальная фаза тока определяется из соотношения:
φ1 = yU1 – yI1, отсюда yU1 =yI1 + j1 = 13°- 24.66°= - 11.66°
Мгновенное значение напряжения первой гармоники
u1= Um1 * Sin (ωt + yU1) = 537 * Sin (ωt – 11.66°) B.
Вторая гармоника.
Для остальных гармоник напряжения расчёты приводим без дополнительных разъяснений.
X2= XC11/ 2 + XL21* 2 - XC31 / 2 = -65/ 2 + 56* 2 - 23 / 2 = 68 Ом.
Z2=![]() =
=![]() =97.6 Ом,
=97.6 Ом,
Im2=1.2 A, Um2= Im2 *Z2=1.2*97.6 =117 B.
U2= Um2/![]() =117 / 1,41 = 83 B.I2= Im2/
=117 / 1,41 = 83 B.I2= Im2/![]() = 1.2 / 1,41 = 0.85 A.
= 1.2 / 1,41 = 0.85 A.
Sin φ2= X2/ Z2= 68/97.6= 0,6967.j2 = 44.16°, Cos φ2 = 0,7173.
P2 = I22 * R2 = 0.852 *70 = 51 Вт.
yU2 =yI2 + j2 = -86°+ 44.16°= - 41.9°
u2= Um2 * Sin (2ωt + yU2) = 117 * Sin (2ωt – 41.9°) B.
Третья гармоника
X3= XC11 /3 + XL11* 3 – XC31 / 3 = - 65 / 3 + 56* 3 - 23 / 3 =139 Ом.
Z3 = ![]() = 156 Ом. Im3 =0.4 A, Um3 = Im3 *Z3 =0.4 *156 =
= 156 Ом. Im3 =0.4 A, Um3 = Im3 *Z3 =0.4 *156 =
= 62.4 B.
U3= Um3/ ![]() =62.4/
=62.4/ ![]() = 44.3 B. I3 = Im3/
= 44.3 B. I3 = Im3/![]() = 0.4 / 1,41 = 0.28 A.
= 0.4 / 1,41 = 0.28 A.
Sin φ3 = X3 / Z3 =139 /156 = 0,891. j3 = 63°. Cos φ3 = 0,454.
P3 = I32 * R = 0.282 *70 = 0.5 Вт.
yU3 =yI3 + j3 = 63°.
u3= Um3 * Sin (3ωt + yU3) =44.3 * Sin (3ωt +63°) B.
Определяем действующие значения тока и напряжения:
I = ![]() =
= ![]() = 5.04 A.
= 5.04 A.
U = ![]() =
= ![]() = 559 B.
= 559 B.
Активная и реактивная мощности цепи:
P = P1+P2+P3=1722+51+0.5=1774 Вт.
Средневзвешенный коэффициент мощности цепи:
Cos Х = Р / (U * I) = 1774/ (559 *5.04) = 0,6296.
Уравнение мгновенных значений напряжения между зажимами цепи:
u=u1+u2+u3=537 * Sin (ωt – 11.66°)+117 * Sin (2ωt – 41.9°)+
+44.3 * Sin (3ωt +63°) B.
Литература
1. Ф.Е. Евдокимов. Теоретические основы электротехники. - М. “Высшая школа “,1981 г.
2. В.С. Попов. Теоретическая электротехника. – М. “Энергия”,
1978 г.
3. Ю.В. Буртаев, П. И. Овсянников. Теоретические основы электротехники.– М. “Энергоатомиздат”, 1984 г.
4. Л.А. Частоедов. Электротехника. - М. “Высшая школа”, 1984 г.
5. М.Ю. Зайчик. Сборник задач и упражнений по теоретической электротехнике. – М. “Энергоатомиздат” , 1988 г.
Похожие работы
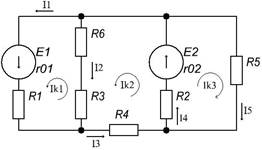
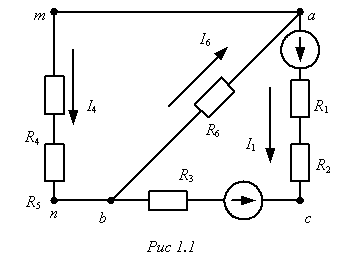
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
... по частям, как в пункте I}= II. В результате получаем закон изменения искомой величины при подаче на вход цепи импульса заданной формы: Расчет и построение графика спектральной плотности прямоугольного импульса Основой спектрального анализа является то, что любой непрерывный сигнал можно представить как периодический с периодом . Энергия ...
чает в себя источники мощности (активные элементы) и приемники (пассивные элементы). В качестве пассивного линейного элемента в цепях постоянного тока выступает резистор, имеющий электрическое сопротивление R. Единица измерения Ом. Величина, обратная сопротивлению, называется электрической проводимостью: G = 1/R. Единица измерения См - сименс. В качестве активных элементов - источников ...

0 комментариев