Навигация
Термодинамические основы термоупругости
1 Термодинамические основы термоупругости
1.1 Термоупругость
Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации ![]() отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
отнесенные к системе прямоугольных осей х1 x2 x3 определяются выражением (1.1.1)
![]() , (1.1.1)
, (1.1.1)
Допускается, что ![]() достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
достаточно мало для того, чтобы термические свойства тела оставались постоянными на том отрезке времени, который нас интересует. Суммарная деформация тела выражается через компоненты вектора перемещения u1 следующим уравнением:
![]() (1.1.2)
(1.1.2)
где ![]() обозначает частную производную
обозначает частную производную![]()
![]() . Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой
. Эта суммарная деформация состоит из термической деформации и упругой деформации, компоненты которой ![]() определяются соотношением (1.1.1)
определяются соотношением (1.1.1)
![]() , (1.1.3)
, (1.1.3)
где τij — компоненты тензора напряжений; величина
θ = τij (1.1.4)
является суммой главных напряжений; λ и μ — упругие постоянные Ламе для тела. Подставляя соотношения (1.1.1) — (1.1.3) — в уравнение
![]()
получим тензорное уравнение
![]() , (1.1.5)
, (1.1.5)
Решая это тензорное уравнение относительно компонентов тензора напряжений, найдем
![]() (1.1.6)
(1.1.6)
где
![]() (1.1.7)
(1.1.7)
обозначает расширение тела и
γ = α(3λ + 2μ). (1.1.8)
Физический закон, выраженный тензорным соотношением (1.1.6), называется законом Дюамеля — Неймана
Термодинамическими переменными, описывающими состояние упругого тела, являются компоненты деформации (1.1.2) и абсолютная температура Т +![]() .
.
Используя методы термодинамики обратимых процессов, Био показал, что энтропия s единицы объема тела определяется соотношением
![]() (1.1.9)
(1.1.9)
где аддитивная постоянная, входящая в определение энтропии, была выбрана таким образом, что энтропия была равна нулю в начальном состоянии. В этом уравнении ρ — плотность тела, с — удельная теплоемкость единицы массы (принимаемая независимой от температуры вблизи равновесной температуры T), и γ определяется формулой (1.1.8). Если ![]() мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
![]() (1.1.10)
(1.1.10)
Таким образом, количество тепла, поглощаемое единицей объема в процессе малых деформаций и малых изменении температуры, определяется формулой
h=Ts = ρс![]() + γTΔ (1.1.11)
+ γTΔ (1.1.11)
Из теории теплопроводности в твердых телах известно, что изменение температуры внутри изотропного тела подчиняется уравнению
![]() (1.1.12)
(1.1.12)
k — коэффициент теплопроводности тела;
q — количество тепла;
выделяемого в единице объема тела. Подставляя выражение (1.1.10) в соотношение (1.1.11), найдем
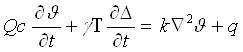 (1.1.13)
(1.1.13)
Если ввести коэффициент температуропроводности
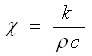 ,
,
то последнее уравнение можно записать в форме
![]() (1.1.14) где
(1.1.14) где
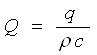 ,
, 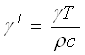
Для того чтобы дополнить систему основных уравнений, присоединим к ней уравнения движения в виде
![]() , (1.1.15)
, (1.1.15)
где (F1 , F2 ,F3) обозначает массовую силу в точке (х1, х2 , х3) и — i-й компонент ускорения д2и/дt2 бес конечно малого элемента, сосредоточенного около этой точки.
Система шестнадцати уравнений (1.1.2), (1.1.6), (1.1.14) и (1.1.15) вместе с соответствующими граничными условиями достаточна для определения изменения температуры и компонентой напряжений и перемещения в случае» когда источники тепла и массовые силы заданы.
Безразмерная форма уравнений. Основные уравнения термоупругости удобно записать в безразмерной форме. Если характерный линейный размер ![]() принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
принять в качестве единицы длины» время τ в качестве единицы времени, температуру начала отсчета T за единицу измерения температуры и модуль сдвига μ принять в качестве единицы измерения, напряжения то в результате найдем, что уравнения (1.1.6), (1.1.14) и (1.1.15) примут соответственно следующую безразмерную форму:
![]() , (1.1.16)
, (1.1.16)
![]() (1.1.17)
(1.1.17)
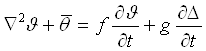 где
где
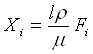 ,
, 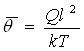
обозначают новые функции и
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При определении а величина ![]() была заменена скоростью с2 распространения S-волн в теле. Величинa
была заменена скоростью с2 распространения S-волн в теле. Величинa ![]() представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде
представляет квадрат отношения скорости Р – волн к скорости S – воли. В зависимости от коэффициента Пуассона величину β можно записать в виде ![]() .
.
Задачи об установившихся состояниях. Если массовые силы и источники тепла не зависят от времени и если поверхностные нагрузки являются статическими нагрузками, то тогда основная система уравнений (1.1.16), (1.1.14) и (1.1.15) примет вид
![]() (1.1.19)
(1.1.19)
![]() , (1.1.20)
, (1.1.20)
![]() (1.1.21)
(1.1.21)
Подставив в уравнение (1.1.19) модуль Юнга Е и коэффициент Пуассона υ, получим следующее уравнение:
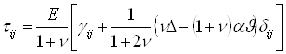 (1.1.22)
(1.1.22)
Для упругого тела, свободного от массовых сил, полагая Fi = 0 и используя формулу
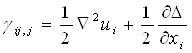
найдем, подставляя соотношение (1.1.22) в уравнение (1.1.21):
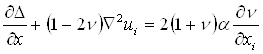 (1.1.23)
(1.1.23)
Для того чтобы решить это уравнение, Гудьер вводит термоупругий потенциал φ, с помощью которого вектор перемещения u1, u2, и3 определяется в виде
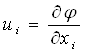 (1.1.24)
(1.1.24)
Подставляя выражение (1.1.24) в уравнение (1.1.23), получаем условие, накладываемое на φ:
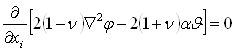
Таким образом, если выбрать φ так, что
![]() , (1.1.25)
, (1.1.25)
где
![]()
то вектор перемещения, определяемый уравнением (1.1.24), является решением уравнений, описывающих установившийся процесс термоупругости.Уравнение (1.1.25) в точности соответствует уравнению Пуассона и хорошо известно, что частный интеграл этого уравнения имеет вид
 (1.1.26)
(1.1.26)
где интегрирование распространяется на все тело.
Напряженное и деформированное состояния, представляемые частным интегралом (1.1.26), требуют не только заданного распределения температуры, но также и определенных поверхностных нагрузок, которые могут быть вычислены посредством выражения (1.1.22) и условии равновесия на границе. Для полного решения задачи требуется лишь определить распределение дополнительных напряжениий, обусловленных равными и прямо противоположными нагрузками на границе, что представляет собой задачу теории упругости при заданных нагрузках на границе. Тот факт, что тело нагрето, не играет роли до тех пор, пока упругие постоянные остаются неизменными. Интегралы типа (1.1.26) были использованы Борхардтом при общем анализе теории термоупругости и при решении некоторых частных задач в случае несимметричных распределений температуры в теле со сферическими или цилиндрическими границами. Распределение напряжений, обусловленное специальным распределением температуры в бесконечном и полубесконечном телах, обсуждалось различными авторами. Имеется очень мало точных решений даже этих уравнений, описывающих установившееся состояние, а те, которые имеются, относятся к сферам и цилиндрам, однако в главе 14 книги Тимошенко и Гудиера «Theory of Elasticity» (New York, 1951) рассматривается несколько приближенных решений инженерных задач, касающихся термических напряжений в пластинах и стержнях
Похожие работы
... отход от классических представлений и понятий и положили начало созданию новой физической картины мира – квантово-релятивистской. Переход от классической физики к современной характеризовался не только возникновением новых идей, открытием новых неожиданных фактов и явлений, а преобразованием ее духа в целом, возникновением нового способа физического мышления, глубоким изменением методологических ...
... циклов. Полезные космические грузы типа солнечных батарей или антенн спутников сейчас используют в основном пиротехнические способы раскрытия, которые создают множество проблем. Использование материалов с памятью формы позволит устранить все эти проблемы, также предоставит возможность неоднократно проверить работоспособность системы еще на земле. Недавнее исследование относительно Ni-Ti сплавов ...
... через окна, без проблем защитит человека от огня и некоторых техногенных происшествий. Многослойное стекло – одно из составляющих частей изолирующих стеклопакетов. Ламинирование не служит для увеличения прочности стекла, его основная функция предотвратить разлетание осколков в разные стороны, путем воздействия эластичной пленки. Так же стоит отметить, что многослойное стекло хорошо защищает от ...
... – Саратов: Изд-во Саратовского университета. –1986. – 153 с. 22. Лапшин В.И., Саутин А.З., Круглов Ю.И., Ильин А.Ф., Масленников А.И. Особенности газотермодинамических и геохимических характеристик Астраханского газоконденсатного месторождения//Теория и практика добычи, транспорта и переработки газоконденсата. Вып. 1. 1999. С. 109-112. 23. Лапшин В.И., Шугаев А.П., Елфимов В.В., Алексеева ...
0 комментариев