Навигация
2 Модель термоупругой среды
2.1 Понятие модели сплошной среды: простые и сложные
Дифференциальные уравнения и соотношения, выражающие законы сохранения массы, импульса, энергии и второй закон термодинамики нужны для общего случая независимо от того, какими конкретными физико-механическими свойствами обладает деформируемая среда, и в силу этого имеют универсальный характер, т.е. справедливы для любых сред. Однако при попытке математического описания движения какой-либо конкретной деформируемой среды (газообразной, жидкой или твердой) довольно легко установить, что имеющихся в распоряжении универсальных дифференциальных уравнений и соотношений не достаточно для составления замкнутой системы уравнений, которая могла бы послужить основой для последующего нахождения единственного решения и получения количественной информации о характере движения и изменения состояния деформируемой среды. При этом очевидна закономерность: количество входящих в составляемую систему уравнений неизвестных величин (характеристических функций) на 6 единиц больше имеющихся в распоряжении уравнений, где 6 — количество независимых компонент симметричных тензоров напряжений и деформаций. Например, приведенная ниже система уравнений адиабатического движения деформируемой среды включает 20 уравнений (одно уравнение неразрывности (2.1.1), три уравнения движения (2.1.2), одно уравнение энергии (2.1.3), три кинематических соотношения взаимосвязи компонент скорости и перемещения (2.1.4), шесть геометрических соотношений (2.1.5) и шесть кинематических соотношений (2.1.6) и 26 неизвестных характеристических функций (плотность, удельная внутренняя энергия, по три компоненты векторов перемещения и скорости, по шесть независимых компонент симметричных тензоров напряжений, деформаций и скоростей деформаций) [53]:
div υ=0, (2.1.1)
, (2.1.2)
, (2.1.3)
, (2.1.4)
, (2.1.5)
, (2.1.6)
Анализ приведенной системы уравнений показывает, что в ней отсутствуют соотношения, учитывающие реакцию деформируемой среды на процесс деформирования и показывающие, какие внутренние напряжения возникают в ней в ответ на деформации. Подобные соотношения в самом общем виде можно записать как
(2.1.7)
Соотношения вида (2.1.7) называются физическими соотношениями, они определяют специфику той или иной деформируемой среды в отношении оказания сопротивления деформированию и тесно связаны с понятием модели сплошной среды.
Модель сплошной среды — это некоторое идеализированное представление реальной деформируемой среды, учитывающее основные ее свойства сопротивления деформированию и подчиняющееся определенному математическому описанию в виде физических соотношений (2.1.7). Выбор модели сплошной среды для реальной деформируемой среды и соответствующий выбор физических соотношений (2.1.7) позволяет составить замкнутую систему дифференциальных (2.1.1)—(2.1.6) и конечных функциональных (2.1.7) уравнений для математического описания движения и внутреннего состояния исследуемой среды.
Под простыми моделями сплошных сред понимаются идеализированные представления реальных деформируемых сред, учитывающие какое-либо одно из основных механических свойств. К числу простых относятся следующие четыре модели: модель идеальной среды (идеальная жидкость или идеальный газ, не способные оказывать сопротивление формоизменению); модель вязкой жидкости (учитывается лишь свойство вязкости); модель упругой среды (принимается во внимание лишь проявление свойства упругости); модель жесткопластической среды (проявляется только свойство пластичности). Рассмотрим перечисленные выше простые модели сплошных сред, придерживаясь следующей последовательности: определение модели, общие соображения относительно сопротивления деформированию данной среды, определяющие уравнения, физические соотношения, примеры использования данной модели при физико-математическом моделировании и ее термодинамические особенности. Упругая (идеально, или совершенно, упругая) среда — это изотропная сплошная среда, сдвиговое и объемное сопротивления которой линейно зависят от деформаций. В качестве определяющих уравнений для модели упругой среды выступают уравнения, устанавливаемые на основе опытных данных по деформированию твердых тел (металлов и их сплавов, пластмасс и т.п.) при малых деформациях. Этим же обстоятельством определяется область практического использования данной модели сплошной среды.
Так, из экспериментов по всестороннему сжатию твердых тел при малых объемных деформациях устанавливается прямо пропорциональная зависимость среднего напряжения от средней деформации, выражаемая уравнением Бриджмена (2.1.8) и определяющая физическое поведение упругой среды.
(2.1.8)
В более общем случае, с учетом влияния температуры, физическое поведение упругой среды описывается уравнением Дюамеля — Неймана:
(2.1.9)
К — модуль объемного сжатия;
— коэффициент линейного теплового расширения материала;
Т и 
— соответственно текущая и начальная температуры материала.
Уравнение Дюамеля — Неймана может быть представлено в более "прозрачном" для понимания виде: 
, показывающем, что вклад в объемную деформацию 
при деформировании индивидуальных частиц упругой среды вносят всестороннее сжатие или растяжение и нагрев, при этом влияние фактора нагрева проявляется в зависимости от коэффициента объемного теплового расширения 
.
Вто же время из экспериментов по кручению тонкостенных металлических труб, в индивидуальных частицах среды реализуется напряженно-деформированное состояние чистого сдвига, устанавливается прямо пропорциональная зависимость касательных напряжений от сдвиговых деформаций, приводящая к выводу о существовании следующей взаимосвязи между девиаторами напряжений деформаций:
(2.1.10)
где G – модуль упругости второго рода (модуль сдвига).
Уравнение (3.21) принимается в качестве определяющего механическое поведение упругой среды. Из уравнения (3.21) следует скалярное определяющее уравнение — прямо пропорциональная зависимость интенсивности напряжений от интенсивности деформаций:
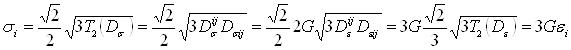
Из определяющих уравнений (3.12)(или (3.20)) и (3.21) следуют физические соотношения для моделей упругой среды,принимающие форму обобщенного закона Гука. Компоненты девиатора напряжений (см. (3.21)) могут быть выражены через компоненты девиатора деформаций как 
. Отсюда в случае выражения среднего напряжения σ через среднюю деформацию ε из уравнения Бриджмена (3.12) следуют прямые физические соотношения в виде зависимостей компонент тензора напряжений от компонент тензора деформаций:
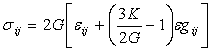(2.1.11)
Обратные физические соотношения (зависимости компонент тензора деформаций от компонент тензора напряжений) получаются аналогичным образам и имеют вид
(2.1.12)
Обобщенный закон Гука описывает все частные проявления упругого поведения деформируемых сред, реализующиеся в простых случаях напряженно-деформированного состояния. Так, для деформированного состояния чистого сдвига (ε12
0,ε11 = ε22 = ε33 = ε13 = ε23 =0) согласно (2.1.12) реализуется напряженное состояние σ12 = 2Gε12,σ11 = σ22 = σ33 = σ13 = σ23 =0 с прямо пропорциональной зависимостью касательных напряжений от сдвиговых деформаций. Деформированному состоянию всестороннего равноосного растяжения или сжатия ε11 = ε22 = ε33 = ε 0, εij = 0 при i j) соответствует такое же напряженное состояние: σ11 = σ22 = σ33 = σ = 3Kε, σ12 = σ13 = σ23 =0.Напряженному состоянию одноосного растяжения (σ11 0, σ22 = σ33 = σ12 = σ13 = σ23 = 0, σ = σ11/3 отвечает трехосное деформированное состояние: εij = 0 при i j и
(2.1.13)
где Е = 18KG/(6K + 2G) — модуль упругости первого рода (модуль Юнга), a v = (ЗК - 2G)/(6K + 2G) — коэффициент Пуассона.
Модуль Юнга Е и коэффициент Пуассона v в дополнение к модулю сдвига G и модулю объемного сжатия К являются еще одной парой упругих характеристик, через которые может быть представлен обобщенный закон Гука. Выражая модуль объемного сжатия и модуль сдвига через модуль Юнга и коэффициент Пуассона как
, 
(2.1.14)
можно получить запись физических соотношений для моделей упругой среды в форме
;
.
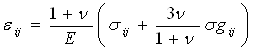Следует отметить, что имеющаяся взаимосвязь между парами упругих характеристик (2.1.14) позволяет ограничиться экспериментальным определением лишь двух из них с последующим расчетом двух других. Наиболее просто определяются из опытов значения модуля Юнга Е (одноосное растяжение образцов) и модуля сдвига G (кручение образцов с реализацией напряженно-деформированного состояния чистого сдвига).
Уравнения (2.1.8), (2.1.10) и (2.1.13) позволяют истолковать физический смысл упругих характеристик G, E, v, К. Как следует из (2.1.10), модуль сдвига G определяет касательные напряжения, возникающие в упругой среде при чистом сдвиге. В соответствии с (2.1.13) модуль Юнга Е определяет продольные деформации, возникающие при одноосном растяжении, а коэффициент Пуассона v — соотношение поперечной и продольной деформаций в этом же случае. Согласно уравнению Бриджмена (2.1.8), модуль объемного сжатия К определяет среднее напряжение в зависимости от объемной деформации в и, напротив, характеризует объемную деформацию, возникающую в частицах упругой среды, когда в них существует давление р = — σ: = Зε = σ/К.
Важным частным случаем модели упругой среды является так называемая несжимаемая упругая среда, объем индивидуальных частиц, которой не изменяется при любом уровне давления (или среднего напряжения). Для такой среды 
, модуль объемного сжатия К = ∞, а коэффициент Пуассона v = 0,5 в соответствии с (2.1.14). Для реальных же твердых тел, обладающих сжимаемостью и по своим свойствам близких к модели упругой среды, коэффициент Пуассона v = 0,2...0,3.
Термодинамические особенности модели упругой среды определяются тем обстоятельством, что процесс адиабатического деформирования ее частиц является обратимым и в случае снятия нагрузок сопровождается самопроизвольным протеканием в обратном направлении с уменьшением до нуля напряжений и деформаций и возвратом в исходное состояние. Для такой среды отсутствует переход механической работы деформации во внутреннюю тепловую энергию (χ = 0), энтропия индивидуальных частиц может изменяться только за счет теплообмена с окружающими частицами:
. Деформирование же упругой среды в адиабатических условиях (
) имеет изоэнтропический характер dS/dt =0.
Под сложными моделями сплошных сред понимаются модели, в которых учитываются два и более основных механических свойства. К числу таких моделей относятся, например, упругопластическая, вязкоупругая, вязкопластическая, упруговязкопластическая среды. В этом разделе рассматривается одна из сложных моделей — модель упругопластической среды, наиболее широко используемая при математическом моделировании процессов деформирования твердых тел. Модель упругопластической среды соответствует твердым телам (главным образом, металлам и их сплавам), которые при нагружении работают упруго, пока не выполняется некоторое предельное условие, называемое условием пластичности, а при дальнейшем нагружении такой среды в ней развиваются не только упругие, но и пластические деформации.
Для реальных упругопластических сред характерны диаграммы механического поведения (диаграммы деформирования) 
подобные диаграмме, приведенной на рис. 1, в для мягкой стали (типа стали 10). В ряде случаев диаграммы деформирования реальных металлов могут несколько отличаться от показанной на рис. 1,в в сторону усложнения (например, включать участок нелинейной упругости) или в сторону упрощения (например, для некоторых металлов отсутствует площадка текучести и после упругого участка сразу происходит переход к участку упрочнения) и включать дополнительные характерные точки: в первом случае такой точкой является предел упругости, больший предела пропорциональности, а во втором — условный предел текучести, соответствующий заданному уровню остаточной пластической деформации. Однако при построении модели упругопластической среды, как правило, пренебрегают такими тонкими особенностями и рассматривают идеализированные диаграммы механического поведения, подобные показанным на рис.1. Наиболее часто в качестве таких идеализированных диаграмм механического поведения рассматриваются диаграммы для идеальной упруго-пластической среды, для которой пределы пропорциональности, упругости, текучести и прочности ассоциируются с одним и тем же значением 
(рис.1,а) и для упругопластической среды с линейным (рис.1,б) или нелинейным (рис. 1, в) упрочнением.
Рисунок 1
Возможными вариантами упрощенных диаграмм механического поведения являются диаграммы идеальной жесткопластической среды (рис.1,г) или жесткопластической среды с упрочнением (рис. 1, д), причем для двух последних случаев характерно отсутствие упругого участка (упругими деформациями по сравнению с пластическими пренебрегают).
Модель упругопластической среды является сложной не только по формальному признаку (принимаются во внимание свойства упругости и пластичности), но и с точки зрения уровня сложности математического описания. Отметим, что в случае малых деформаций (превышающих упругие, но соизмеримых с ними) модель упругопластической среды хорошо описывается деформационной теорией пластичности (теория малых упругопластических деформаций). При больших (конечных) деформациях для описания поведения упругопластических сред более предпочтительна теория пластического течения.
Похожие работы
... отход от классических представлений и понятий и положили начало созданию новой физической картины мира – квантово-релятивистской. Переход от классической физики к современной характеризовался не только возникновением новых идей, открытием новых неожиданных фактов и явлений, а преобразованием ее духа в целом, возникновением нового способа физического мышления, глубоким изменением методологических ...
... циклов. Полезные космические грузы типа солнечных батарей или антенн спутников сейчас используют в основном пиротехнические способы раскрытия, которые создают множество проблем. Использование материалов с памятью формы позволит устранить все эти проблемы, также предоставит возможность неоднократно проверить работоспособность системы еще на земле. Недавнее исследование относительно Ni-Ti сплавов ...
... через окна, без проблем защитит человека от огня и некоторых техногенных происшествий. Многослойное стекло – одно из составляющих частей изолирующих стеклопакетов. Ламинирование не служит для увеличения прочности стекла, его основная функция предотвратить разлетание осколков в разные стороны, путем воздействия эластичной пленки. Так же стоит отметить, что многослойное стекло хорошо защищает от ...
... – Саратов: Изд-во Саратовского университета. –1986. – 153 с. 22. Лапшин В.И., Саутин А.З., Круглов Ю.И., Ильин А.Ф., Масленников А.И. Особенности газотермодинамических и геохимических характеристик Астраханского газоконденсатного месторождения//Теория и практика добычи, транспорта и переработки газоконденсата. Вып. 1. 1999. С. 109-112. 23. Лапшин В.И., Шугаев А.П., Елфимов В.В., Алексеева ...
0 комментариев