Навигация
Построение задачи термоупругости
1.2 Построение задачи термоупругости
В общем случае постановка задачи термоупругости заключается в следующем. Необходимо при заданных механических и тепловых воздействиях определить 16 функций координат хR и времени t: шесть компонентов тензора напряжения ![]() шесть компонентов тензора деформации ε - три компонента вектора перемещения
шесть компонентов тензора деформации ε - три компонента вектора перемещения ![]() и температуру Т, удовлетворяющих: трем уравнениям движения (1.2.1); шести соотношениям между напряжениями и деформациями (1.2.2) или (1.2.3); шести соотношениям между деформациями и перемещениями (1.2.4); уравнению теплопроводности (1.2.5), при определенных начальных и граничных условиях.
и температуру Т, удовлетворяющих: трем уравнениям движения (1.2.1); шести соотношениям между напряжениями и деформациями (1.2.2) или (1.2.3); шести соотношениям между деформациями и перемещениями (1.2.4); уравнению теплопроводности (1.2.5), при определенных начальных и граничных условиях.
![]() (1.2.1)
(1.2.1)
ρ – плотность,
![]() – силы инерции.
– силы инерции.
![]() (1.2.2)
(1.2.2)
где λ и μ – коэффициенты Ляме при изотермической деформации.
![]() (1.2.3)
(1.2.3)
Е – изотермический модуль упругости;
![]() - коэффициент Пуассона.
- коэффициент Пуассона.
![]() (1.2.4)
(1.2.4)
где ![]() – вектор перемещения.
– вектор перемещения.
![]() (1.2.5)
(1.2.5)
S – плотность энергии;
![]() – коэффициент теплопроводности;
– коэффициент теплопроводности;
![]() – удельная мощность (количество тепла, произведенного за единицу времени в единицу объема) источников тепла.
– удельная мощность (количество тепла, произведенного за единицу времени в единицу объема) источников тепла.
Начальные условия обычно задаются в виде распределений компонентов вектора перемещения ![]() , их скоростей
, их скоростей ![]() и температуры Т во всей области V упругого тела:
и температуры Т во всей области V упругого тела:
![]() ,
, ![]() ,
, ![]() при t = 0. (1.2.6)
при t = 0. (1.2.6)
Здесь и дальше обозначения gi(xR), hi(xR), f(xR) означают функции всех координат хR (R — 1, 2, 3) в рассматриваемой области.
Граничные условия на поверхности Ω упругого тела, ограничивающей его объем V, складываются из механических и тепловых условий.
Механические граничные условия задаются либо в перемещениях
![]() при t >0, (1.2.7)
при t >0, (1.2.7)
либо в напряжениях
![]() при t >0, (1.2.8)
при t >0, (1.2.8)
![]() — компоненты вектора поверхностной силы;
— компоненты вектора поверхностной силы;
пj — компоненты единичного вектора внешней нормали к поверхности Ω.
В качестве теплового граничного условия применяется одно из граничных условий теории теплопроводности. Механические и тепловые граничные условия могут быть также смешанными. На одной части поверхности механические граничные условия могут быть заданы в перемещениях (1.2.7), а на другой — в напряжениях (1.2.8). Тепловое граничное условие на одной части поверхности тела задается, например, температурой, а на другой — законом конвективного теплообмена с окружающей средой.
Система уравнений (1.2.1), (1.2.2) или (1.2.3), (1.2.4) и (1.2.5) при указанных начальных граничных условиях описывает связанную нелинейную задачу термоупругости.
При ![]() << I значения упругих и термических коэффициентов и удельных теплоемкостей предполагаются постоянными, вместо уравнения (1.2.5) применяется уравнение теплопроводности (1.2.9), и связанная задача термоупругости становится линейной.
<< I значения упругих и термических коэффициентов и удельных теплоемкостей предполагаются постоянными, вместо уравнения (1.2.5) применяется уравнение теплопроводности (1.2.9), и связанная задача термоупругости становится линейной.
![]() (1.2.9)
(1.2.9)
Доказано, что для области V, свободной от объемных сил и источников тепла, решение системы уравнений (1.2.1), (1.2.2), (1.2.3), (1.2.5) при начальных и граничных условиях, заданных через перемещения и температуру, является единственным. Это доказательство можно обобщить и на другие механические и тепловые воздействия и граничные условия.
Составим для этой задачи уравнения движения в перемещениях. Выражая в уравнениях (1.2.1) напряжения через деформации по формуле (1.2.2) и учитывая, что члены, содержащие εRR и T, сохраняются только при i — j, получаем
![]() . (1.2.10)
. (1.2.10)
В этом уравнении деформации заменяем перемещениями. Заменяя j немым индексом R и учитывая, что ![]() , находим
, находим
![]() (1.2.11)
(1.2.11)
Уравнения (1.2.11) совместно с уравнением (1.2.9) при определенных начальных и граничных условиях описывают изменение в пространстве и во времени поля деформации и температурного поля. Представим эти уравнения в векторной форме:
![]() grad div
grad div ![]() grad
grad ![]() (1.2.12)
(1.2.12)
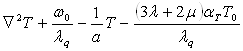 div
div![]() (1.2.13)
(1.2.13)
где 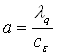 коэффициент температуропроводности.
коэффициент температуропроводности.
Похожие работы
... отход от классических представлений и понятий и положили начало созданию новой физической картины мира – квантово-релятивистской. Переход от классической физики к современной характеризовался не только возникновением новых идей, открытием новых неожиданных фактов и явлений, а преобразованием ее духа в целом, возникновением нового способа физического мышления, глубоким изменением методологических ...
... циклов. Полезные космические грузы типа солнечных батарей или антенн спутников сейчас используют в основном пиротехнические способы раскрытия, которые создают множество проблем. Использование материалов с памятью формы позволит устранить все эти проблемы, также предоставит возможность неоднократно проверить работоспособность системы еще на земле. Недавнее исследование относительно Ni-Ti сплавов ...
... через окна, без проблем защитит человека от огня и некоторых техногенных происшествий. Многослойное стекло – одно из составляющих частей изолирующих стеклопакетов. Ламинирование не служит для увеличения прочности стекла, его основная функция предотвратить разлетание осколков в разные стороны, путем воздействия эластичной пленки. Так же стоит отметить, что многослойное стекло хорошо защищает от ...
... – Саратов: Изд-во Саратовского университета. –1986. – 153 с. 22. Лапшин В.И., Саутин А.З., Круглов Ю.И., Ильин А.Ф., Масленников А.И. Особенности газотермодинамических и геохимических характеристик Астраханского газоконденсатного месторождения//Теория и практика добычи, транспорта и переработки газоконденсата. Вып. 1. 1999. С. 109-112. 23. Лапшин В.И., Шугаев А.П., Елфимов В.В., Алексеева ...
0 комментариев