Навигация
О характеристичности молекулярных колебаний
15917
знаков
4
таблицы
8
изображений
6.3.1. О характеристичности молекулярных колебаний.
Колебания различных химических связей обладают высокой степенью индивидуальности. Это свойство называют характеристичностью. В колебательных спектрах частота и нередко даже графический вид колебательной полосы (или линии) поглощения какой-то определённой химической связи или группы (органического алкильного радикала или иного молекулярного фрагмента) хорошо воспроизводятся в спектрах различных молекул, содержащих эти группы атомов. Эта индивидуальность является основой аналитического применения колебательной спектроскопии. Характеристики молекулярных колебаний можно получить с помощью различных методов спектроскопии инфракрасного (ИК) поглощения или спектроскопии комбинационного рассеяния (КР).
Диаграмма энергетических уровней и графики волновых функций осциллятора.
Уровни гармонического осциллятора согласно (6.8) эквидистанты, и соседние (Dv=1) отстоят на hn, где n собственная частота молекулярного колебания.
6.4. Качественное сравнение волновых функций одномерного ящика и осциллятора выявляет их качественное сходство. Число пучностей и узлов волновых функций увеличивается с номером уровня. Это свойство общее для всех квантовых систем.
6.5. Трёхмерный потенциальный «ящик». Модель одномерного «ящика» легко обобщается для трёхмерного движения в замкнутом пространстве параллелепипеда или куба. Рассмотрим для простоты куб с ребром L . Переменные независимы, и гамильтониан вида
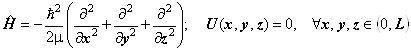.(6.9)
ведёт к аддитивной энергии и мультипликативным волновым функциям:
. (6.10)
(6.11)
6.6. Пространственное вращение. Общие свойства момента импульса.
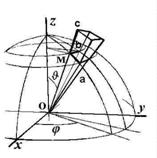
При свободном вращении линейной молекулы относительно центра масс потенциальная энергия нулевая. Оператор кинетической энергии следует представить в шаровой системе координат.
6.6.1. Краткое содержание. Жёсткий ротатор и его уравнение Шрёдингера. Шаровые координаты (r, J, j). Элемент объёма. Лапласиан и уравнение Лапласа в шаровых координатах. Разделение переменных. Роль симметрии в выборе радиальной части общего решения. Радиальная и угловая части уравнения Шрёдингера и вид общего решения. Угловая часть уравнения Лапласа (уравнение Лежандра) и операторное уравнение для момента импульса. Квадрат модуля и проекция на ось вращения в шаровых переменных. Квантование модуля и квантование проекции момента импульса ротатора. Уровни энергии и их вырождение.
|
|
Радиальная переменная r
Угол широты J
Угол долготы j
|
Декартовы координаты:
Элемент объёма в шаровых переменных (см. рис.:
.(6.12)
Во многих задачах достаточно выделить элемент объёма, не зависящий от направления, и имеющий вид тонкого поверхностного слоя на шаре. В таком случае, избавляясь от угловых аргументов и оставляя лишь радиальную переменную, получаем сферический элемент объёма
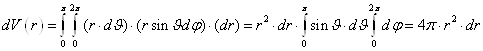.(6.13)
6.6.2. Лапласиан. Очень важным свойством лапласиана является его симметрия ко взаимным перестановкам декартовых координат.
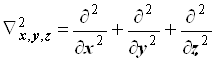(6.14)
Простейшее дифференциальное уравнение, в котором лапласиан играет основную роль - уравнение Лапласа. Это дифференциальное уравнение в частных производных второго порядка. В различные квантово-механические задачи о сферических системах лапласиан входит в качестве основного оператора. Симметрия конкретной системы предопределяет вид координат, к которым следует преобразовать лапласиан, а далее и вид решений тех дифференциальных уравнений, у которых уравнение Лапласа можно выделить в качестве однородной части. Таковы задачи о сферически симметричных движениях. В шаровых координатах лапласиан оказывается составленным из трёх независимых компонент-операторов, каждый из которых преобразует лишь одну из трёх независимых пространственных переменных.
6.6.3. Перевод лапласиана в шаровые координаты можно осуществить, используя различные схемы. В сферических координатах он выглядит довольно внушительно, но при ближайшем рассмотрении оказывается достаточно простой конструкцией. Несложные, но длительные, преобразования приводят к следующей формуле:
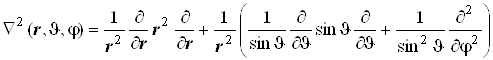. (6.15)
Упрощая, выделим вначале операторы чисто радиальный и чисто угловой:
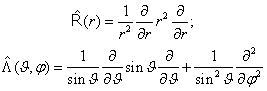.(6.16)
6.6.4. Операторные компоненты лапласиана. Первое слагаемое активно только к радиальной переменной, второе же - к угловым аргументам и оно называется оператором Лежандра. Лапласиан получает вид
. (6.17)
6.6.5 Угловой оператор - оператор Лежандра далее также разделяется на два независимых оператора. Один из них действует на переменную широты J, а второй - на переменную долготы j, так что получается:
. (6.18)
Похожие работы
... ;; он-то и представляет собой численное значение искомой физической величины. Резюме. Выражения 4.3 и 4.4 настолько важны, что без них было бы затруднительно построить математический аппарат квантовой механики. 4.2. О структуре операторного уравнения Способ расчёта динамических переменных из волновой функции оказывается настолько общей, что затрагивает самые важные вопросы о способах ...
... при наличии сил, действующих на частицу, вместо Е в уравнение (16) нужно ввести кинетическую энергию частицы Т = Е –U. Произведя такую замену, мы придем к уравнению (12). Приведенные нами рассуждения не могут рассматриваться как вывод уравнения Шрёдингера. Их цель — пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности ...
... числу l. Энергетические уровни АО многоэлектронного атома (правило Клечковского-Маделунга): “Уровни АО многоэлектронного атома возрастают с ростом суммы квантовых чисел (n+l), а при равных значениях (n+l) ниже лежит уровень с меньшим n”. Экранирование ядра. Одноэлектронный подход к проблеме строения многоэлектронного атома. n+l N,l АО n+l n,l АО n+l n,l АО n+l n,l АО n+l n,l АО ...
... Модель атома водорода 1926- Шрёдингер-Волновое уравнение 1927- Гейзенберг-Соотношение неопределённостей. 1983- Туннельный микроскоп (...Академик В.Гинзбург (ФИАН): “Ну и дожили!”) Раздел 1. Экспериментальные основы квантовой механики. Волны материи. Простейшие полуклассические модели движений Содержание: Движение частицы и движение сплошной среды. Корпускула и волна. Излучение и вещество ...
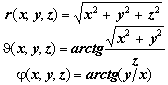
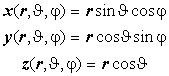
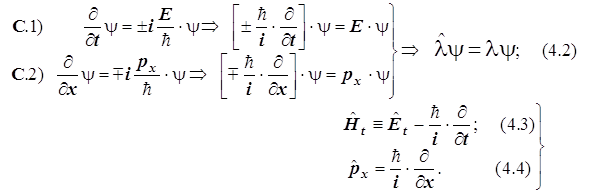
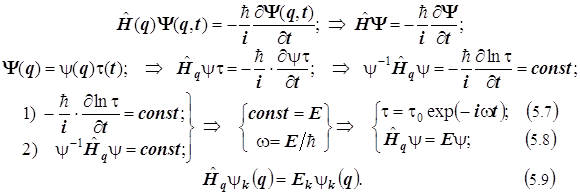
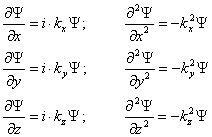
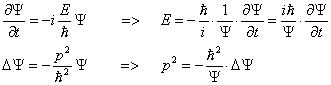
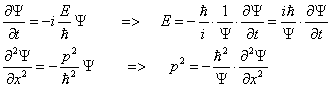
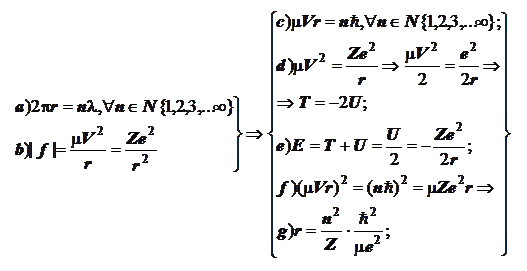
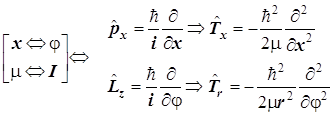
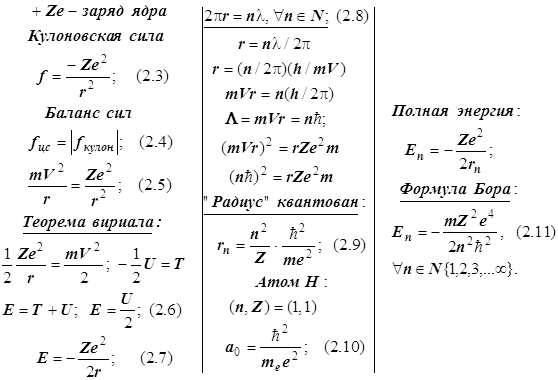
0 комментариев