Введение в аксиоматику квантовой механики

Введение в аксиоматику квантовой механики

Происхождение операторов динамических величин

Содержание:

Уравнение плоской бегущей волны материи.

Операторы импульса и энергии.

Общая схема вычислений физических наблюдаемых в квантовой механике.

4.1. Уравнение плоской бегущей волны материи

Для построения математической схемы квантовой механики необходимо расширить представления о волнах материи. Волны Де Бройля позволяет наиболее экономно показать, как появляются на свет Божий операторы импульса (p) и полной энергии (H), поясняя, что же это такое - операторные уравнения на собственные значения и их смысл. Однако показать – вовсе не означает доказать! ... Обратимся к цепочке рассуждений...

4.1.1. Плоская световая волна

(элекромагнитное поле) описывается уравнениями:

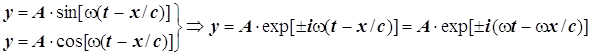
4.1.2. Плоская волна материи:

A)        Подстановки E = ћw = mc² ; Þ w = mc²/ћ = pc/ћ; Þ w = E/ћ приводят к формуле

плоской волны материи:

Это выражение называется волновой функцией системы (плоской волны материи). Она зависит от двух переменных - времени и координаты. Волновая функция считается универсальным источником динамической информации о системе.

Это напоминает термодинамику. Посредством определённых преобразований и действий над термодинамическими функциями состояния можно вычислить прочие термодинамические свойства. Аналогично в квантовой механике из волновой функции системы можно определёнными действиями можно извлечь все её динамические характеристики. Волновая функция является функцией квантово - механического состояния системы.

Энергия и импульс получаются из волновой функции с помощью дифференцирования по разным переменным – времени и координате. Общая схема вычисления представлена формулой 4.2.

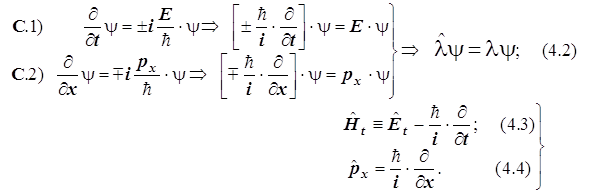
Слева от знака равенства волновая функция Y подвергается совокупности преобразований. Вся совокупность действий, извлекающих эту физическую величину, сгруппирована в один оператор, его символ. Справа от знака равенства результатом преобразований является она же (Y) с точностью до численного множителя ; он-то и представляет собой численное значение искомой физической величины.

Резюме. Выражения 4.3 и 4.4 настолько важны, что без них было бы затруднительно построить математический аппарат квантовой механики.

4.2. О структуре операторного уравнения

Способ расчёта динамических переменных из волновой функции оказывается настолько общей, что затрагивает самые важные вопросы о способах человеческого познания. Итак предмет нашего исследования - операторное уравнение (4.2). Перечислим то, что представляется особо важным.

Содержание:

Общая схема расчётов динамических переменных и структура операторных уравнений квантовой механики. Эксперимент и теория. Измерения и уравнения. Объекты и образы. Система и прибор, волновая функция и оператор. Микросистема и макроприбор, структура операторов. Опыт и теория: информация и организация. Идеальный опыт и операторное уравнение.

Бросается в глаза, что весь алгоритм вычисления динамической переменной разделяется знаком равенства на две части. Такое имеет место в любых вычислениях, знак равенства обязателен при записи уравнений, но здесь активную роль играет само понятие преобразования – понятие оператора.

Все действия слева от знака равенства сгруппированы в один-единственный оператор. Он определяет всю программу действий для достижения результата.

Сам же результат представлен численным множителем справа от знака равенства.

В обеих частях равенства присутствует волновая функция. Слева она объект преобразования, справа - неизменный объект, не претерпевший изменений.

Все эти признаки допускают очень простую и наглядную интерпретацию, самым тесным образом отражающую способы познания человеком окружающего мира. Главное в ней понятие объекта и образа-отображения. В таком случае в нашем понимании важную роль играет каждая деталь...

4.3. Рассмотрим операторное уравнение как образ идеального эксперимента

Волновая функция это образ исследуемой микросистемы.

Оператор, действием которого извлекается искомая величина, есть образ макроскопического прибора, настроенного на измерение конкретной искомой физической величины.

Знак равенства разделяет эксперимент на два качественно разных этапа. Исходный, стартовый этап, предшествующий измерению, изображён выражением слева от знака равенства. На завершающем этапе достигается количественная информация о системе, получено численное значение измеренной величины (справа от знака равенства).

Волновая функция в эксперименте остаётся неизменной, и это отражает простейшее обязательное качество идеального опыта – измерение не должно изменять систему. Иначе невозможно идентифицировать итоги опыта, результат измерения нельзя отнести ни какой-либо конкретной ситуации, ни к какому-либо состоянию, и нельзя вообще сказать, к той ли системе вообще данный результат относится.

При такой точке зрения следует постулировать некоторый минимальный набор операторов и далее определить правило составления оператора любой сколь-угодно более сложной величины.

Раздел 5. Основные понятия и постулаты квантовой механики

Содержание:

Система постулатов квантовой механики.