Навигация
Электрические цепи постоянного и переменного тока
1. Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока
1.1 Расчет линейных электрических цепей постоянного тока
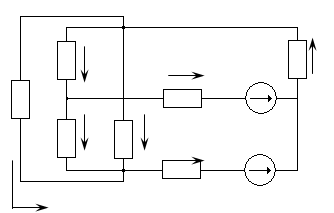
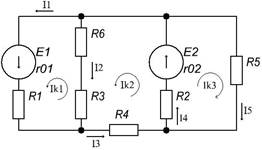
Для электрической цепи, изображенной на (рис. 1.1), выполнить следующее:
1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
2) определить токи во всех ветвях схемы, используя метод контурных токов;
3) определить токи во всех ветвях схемы на основании метода наложения;
4) составить баланс мощностей для заданной схемы;
5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить;
6) определить ток во второй ветви методом эквивалентного генератора;
7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Дано:
E1=20 В, E2=30 В, R1=64 Ом,
R2=43 Ом, R3=31 Ом, R4=25 Ом,
R5=52 Ом, R6=14 Ом, r01=1 Ом,
r02=2 Ом.
Определить: I1 ,I2 ,I3 ,I4 ,I5.

рис. 1.1
1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.
Произвольно задаемся направлением токов в ветвях цепи I1,I2,I3,I4,I5.
Составляем систему уравнений (в системе должно быть стока уравнений, скока в цепи ветвей). В нашей цепи пять ветвей, значит, в системе будет пять уравнений. Сначала составляем уравнение по первому закону Кирхгофа. В цепи с n узлами будет (n-1) уравнений, в нашей цепи три узла, значит, будет два уравнения. Составляем два уравнения, для двух произвольных узлов.
узел D: I3=I1+I2
узел F: I4=I3+I5
Теперь составляем недостающие три уравнения для трех независимых контуров. Чтобы они были независимыми, надо в каждый контур включить хотя бы одну ветвь, не входящую в предыдущую.
Задаемся обходам каждого контура и составляем уравнения по второму закону Кирхгофа.
Контур ABCD – обход против часовой стрелки
E1=I1(R1+r01)-I2(R3+R6)
Контур CDFE – обход против часовой стрелки
E2=I2(R3+R6)+I3R4+I4(R2+r02)
Контур EGHF – обход по часовой стрелке
E2=I4(R2+r02)+I5R5
ЭДС в контуре берется со знаком "+", если направление ЭДС совпадает с обходом контура, если не совпадает – знак "-".
Падения напряжения на сопротивления контура, берется со знаком "+", если направления тока в нем совпадает с обходом контура со знаком "-", если не совпадает.
Мы получили систему из пяти уравнений с пятью неизвестными:
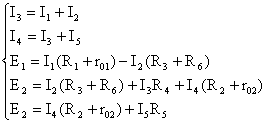 .
.
Решив систему, определим величину и направление тока во всех ветвях схемы.
Если при решении системы ток получается со знаком "-", значит его действительное направление обратно тому направлению, которым мы задались.
2) Определить токи во всех ветвях схемы, используя метод контурных токов.
В заданной цепи можно рассмотреть три контура-ячейки (ABDC, CDFE, EGHF) и вести для них контурные токи Ik1, Ik2, Ik3.
Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.
Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.
На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:
стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках (направление обхода контуров принимаем таким же);
составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.
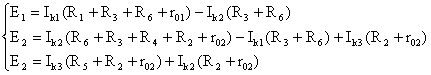 .
.
Подставляем численное значение ЭДС и сопротивлений:
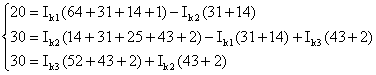
или
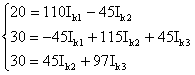
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3.
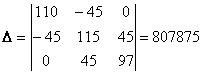 ;
; 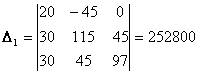 ;
;
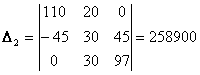 ;
; 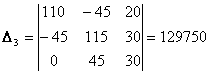 .
.
Вычислим контурные токи:
![]() ;
;
![]() ;
;
![]() .
.
Вычислим действительные токи:
| I1=Ik1=0,313A; | I2=Ik2-Ik1=0,32-0,313=0,007A; |
| I3=Ik2=0,32A; | I4=Ik2+Ik3=0,32+0,161=0,481A; |
| I5=Ik3=0,161A. |
3) Определить токи во всех ветвях схемы на основании метода наложения.
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
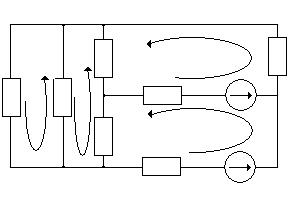
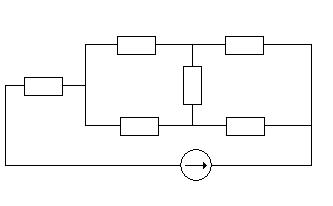
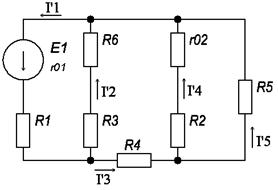
а) Определить частные токи от ЭДС E1, при отсутствии ЭДС E2, т.е. рассчитать цепь по рисунку 1.2
Показываем направление частных токов от ЭДС E1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания".
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() ;
;
![]() Ом;
Ом;
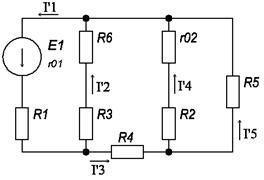
рис 1.2
![]() Ом;
Ом;
![]() Ом.
Ом.
Ток источника:
![]() А.
А.
Применяя закон Ома и первый закон Кирхгофа, вычисляем токи ветвей.
![]() ;
;
![]() В;
В;
![]() В;
В;
![]() А;
А;
![]() А;
А;
![]() В;
В;
![]() В;
В;
![]() А;
А; ![]() А
А
Токи ветвей:
| I1’=I1=0,226A; | I2’=I6,5=0,123A; |
| I3’=I4=0,103A; | I4’=I2,02=0,066A; |
| I5’=I5=0,057A. |
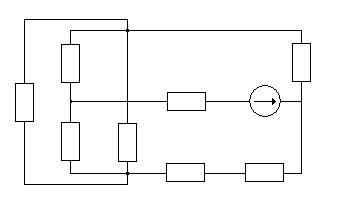
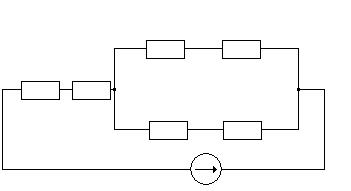
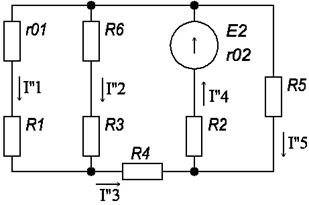
б) Определяем частные токи от ЭДС E2 при отсутствии ЭДС E1, т.е. рассчитываем простую цепь по рисунку 1.3.
Показываем направление частных токов от ЭДС E2 и обозначаем их буквой I с двумя штрихами (I’’).
Рассчитываем общее сопротивление цепи:
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом

рис 1.3
![]() Ом
Ом
![]() Ом
Ом
Ток источника:
![]() А
А
Применяя закон Ома и первый закон Кирхгофа, вычисляем токи ветвей:
![]() ;
; ![]() В;
В;
![]() В;
В;
![]() А;
А;
![]() А;
А;
![]() В;
В;
![]() В;
В;
![]() А;
А;
![]() А;
А;
Токи ветвей:
| I1’’=I1,01=0,106A; | I2’’=I3,6=0,154A; |
| I3’’=I4=0,196A; | I4’’=I2=0,423A; |
| I5’’=I5=0,277А. |
Вычисляем токи ветвей исходной цепи (рис 1.1), выполняя алгебраическое сложение токов, учитывая их направления:
| I1=I1’+I1’’=0,226+0,106=0,332А; | I2=I2’-I2’’=0,123-0,154= -0,031А; |
| I3=I3’+I3’’=0,103+0,196=0,229А; | I4=I4’+I4’’=0,66+0,423=0,489А; |
| I5=I5’-I5’’=0,057-0,227= -0,17А. |
Знак "-" говорит о том, что ток течет в обратном направлении которого мы задались в пункте а).
4) Составить баланс мощностей для заданной схемы.
Источник E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи пишется так:
E1I1+E2I4=I12(R1+r01)+I22(R3+R6)+I32R4+I42(R2+r02)+I52R5.
Подставляем числовые значения и вычисляем:
20ּ0,332+30ּ0,489=0,3322ּ65+0,0312ּ45+0,2992ּ25+0,4892ּ45+0,172ּ52
21,31Вт=21,706Вт
С учетом погрешностей баланс мощностей получился.
5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.
| Ток ветвей Метод расчета | I1, А | I2, А | I3, А | I4, А | I5, А |
| метод контурных токов | 0,313 | 0,007 | 0,320 | 0,481 | 0,161 |
| метод наложения | 0,332 | 0,031 | 0,229 | 0,489 | 0,170 |
Расчет токов ветвей обоими методами с учетом ошибок вычислений примерно одинакова.
6) Определить ток во второй ветви методом эквивалентного генератора.
Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.
Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2 служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.4).
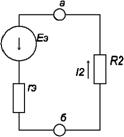
рис 1.4
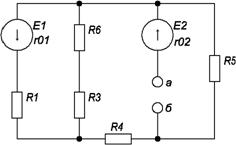
рис 1.5
На схеме искомый ток I2 определим по закону Ома для замкнутой цепи:![]() , где Eэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ=Uxx - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.5), т. е. при отключенном потребителе R2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину:
, где Eэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ=Uxx - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.5), т. е. при отключенном потребителе R2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину:
![]() А.
А.
Зная Ixx величины сопротивлений и ЭДС, в схеме можно определить Uxx как разность потенциалов между клеммами а и б. Для этого потенциал точки а будем считать известным и вычислим потенциал точки б.
φб=φа+E2-IxxּR5 тогда Uxx=φб-φа=E2-IxxּR5=30-0,141ּ52=22,668В
Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.6), при этом ЭДС Е1 и E2 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме остаются.
Вычисляем эквивалентное сопротивление схемы (рис 1.6) относительно зажимов а и б:
 Ом
Ом
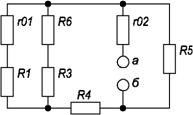
рис 1.6
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:
![]() А.
А.
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Возьмем контур ABFE. Зададимся обходом контура против часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю, φA=0 (рис. 1.1). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А.
φA’=φA+E1-I1r01=0+20-0,313ּ1=19,687 В
φB=φA’-I1R1=19,687-0,313ּ64=-0,345 В
φF=φB-I3R4= -0,345-0,32ּ25=-8,345 В
φF’=φF-I4R2=-8,345-0,481ּ43=-29,028 В
φE=φA=φF’+E2-I4r02= -29,028+30-0,481ּ2=0 В
Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака.
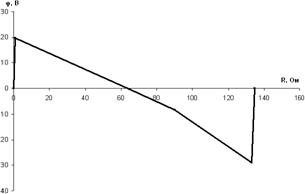
рис.1.7
Похожие работы
... конструкция изделия. Все принятые конструкторские решения подкреплены соответствующими расчетами. 1. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ Кнопка предназначена для коммутации электрических цепей постоянного и переменного тока низкой частоты в стационарных электронных аппаратах и относится к коммутационным устройствам ручного управления. Согласно техническому заданию кнопка должна обеспечивать ...
... , внешнее магнитное поле, частота измеряемого переменного тока. Электромагнитные приборы благодаря простоте, дешевизне и надежности широко применяют для измерения токов и напряжений в сильноточных цепях постоянного и переменного тока промышленной частоты (50 и 400 Гц). Большинство электромагнитных амерметров и вольтметров выпускают в виде щитовых приборов различных класса 1,5 и 2,5. Имеются ...
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
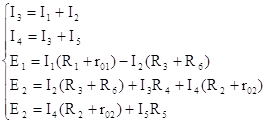

0 комментариев