Навигация
Моделирования пластической деформации ГПУ-кристаллов
49212
знаков
24
таблицы
4
изображения
2. Моделирования пластической деформации ГПУ-кристаллов
Автором была создана программа для изучения пластичности в двумерных кристаллах. Двумерные системы были выбраны, чтобы обойти проблемы, связанные с высокими требованиями к вычислительным ресурсам в случае трехмерных систем и визуализацией результатов вычислений. Для решения уравнений движения использовался алгоритм Верле со скоростью. В качестве потенциала взаимодействия между атомами был выбран потенциал Леннарда-Джонса. При моделировании вычислительная ячейка растягивалась вдоль умножением ее продольного размера на каждом шаге по времени на масштабный множитель (1+ε), где ε – малое число (0.00001), выбранное так, чтобы обеспечить требуемую скорость деформации. Координаты атомов при этом не менялись, т.е. при этом вводился зазор между атомами в смежных ячейках моделирования. При этом нагрузка прикладывалась к торцам кристалла, что лучше соответствует эксперименту. Поперечный размер системы контролировался с помощью динамического уравнения (12). Перед деформацией система приводилась в равновесное состояние с заданной температурой коротким прогоном с помощью МД. При вычислении кривых напряжение-деформация проводилось усреднение напряжения по атомам всей системы. С помощью закона сохранения энергии контролировалась правильность работы программы. Для наблюдения за временной эволюцией деформируемого кристалла использовалась анимация. Блок-схема программы приведена ниже.
| Задание входных данных · Шаг по времени · Число шагов по времени · Число атомов по x (направление деформации) · Число атомов по y · Скорость деформации ε · Температура · Тип решетки (гексагональная) · Ориентация решетки · Граничные условия (периодические) · Потенциал | ||
| Задание начальных значений · Начальные смещения атомов · Начальные скорости атомов | ||
| Достижение равновесного состояния с заданной температурой | ||
| Цикл по атомам (Вычисление начального ускорения) | ||
| Сила Fi, действующая на i-тый атом = сумме сил, действующих со стороны соседних атомов. Ускорение i-того атома ai (t) = Fi/mi | ||
| Конец цикла по атомам | ||
| Цикл по времени (Траектория + растяжение) | ||
| Цикл по атомам (Вычисление нового положения и промежуточной скорости) | ||
|
| ||
| Конец цикла по атомам | ||
| Проверка граничных условий | ||
| Растяжение | ||
| Цикл по атомам (Вычисление нового ускорения и новой скорости ) | ||
| Сила Fi, действующая на i-тый атом = сумме сил, действующих со стороны соседних атомов. Ускорение i-того атома ai (t+Δt) = Fi/mi
| ||
| Конец цикла по атомам | ||
| Контроль параметров · деформация · напряжение · температура | ||
| Конец цикла по времени | ||
| Визуализация | ||
Программа позволяет проводить как обычную МД, так и использовать процедуру минимизации. Программа позволяет исследовать влияние ориентации кристалла, скорости деформирования и температуры на процесс деформирования. Она также позволяет использовать свободные и периодические граничные условия на боковых, относительно растяжения, сторонах кристалла.
С помощью программы проведено моделирование пластического деформирования двумерных кристаллов с гексагональной решеткой. Такие решетки характерны для базисной плоскости ГПУ кристаллов и для плоскости (111) ГЦК кристаллов. Начальная температура 
0.025
. На рис.3 приведена сумма полной энергия кристалла и произведенной над ним работы (на один атом кристалла) как функция времени. Видно, что с точностью до 5 знака эта величина сохраняется, что свидетельствует о правильности работы программы.
Рис.3 Зависимость сумма полной энергия кристалла и произведенной над ним работы (на один атом кристалла) как функция времени.
На рис.4 приведено напряжение, поперечное относительно направления растяжения, как функция времени. Видно, что оно почти все время поддерживается невысоким. Это свидетельствует о правильности выбранного алгоритма регулирования ширины ячейки моделирования.
Рис.4 Зависимость напряжения, поперечного относительно направления растяжения, от времени.
Наконец, на рис.5 приведена кривая напряжение-деформация. Эта кривая полностью соответствует экспериментальным кривым напряжение-деформация для совершенных кристаллов.
Рис.5 Кривая растяжения совершенного кристалла
На этой кривой можно выделить несколько стадий в деформировании кристалла [18,19]. На первой, упругой стадии, происходит накопление энергии. Затем, по мере роста напряжения кристалл переходит в нелинейную область, в конце которой появляются дислокации. Начинается сброс напряжения, который заканчивается появлением полос скольжения, которые и обеспечивают дальнейший сброс напряжения. Затем происходит частичное упрочнение кристалла с последующими сбросами напряжения. На этой стадии происходит накопление вакансий, их слияние в вакансионные поры. На последней стадии поры, объединяясь, дают начало трещине, которая, развиваясь, разрывает кристалл. На рис.6-11 даны изображения кристалла, которые иллюстрируют описанную выше стадийность пластического деформирования и разрушения кристалла.
Заключение
1. Изучен метод молекулярной динамики со всеми его важнейшими ингредиентами: потенциал взаимодействия, граничные условия, алгоритм интегрирования по времени, задание начальных условий, контроль термодинамических параметров в процессе моделирования, контроль достижения термодинамического равновесия, измерение физических величин. Изучены особенности применения метода молекулярной динамики к исследованию пластичности реакторных материалов.
2. Создана программа для изучения пластичности в кристаллах. Создана программа визуализации процесса пластической деформации и разрушения кристаллов. Предложен новый подход к моделированию растяжения кристаллов, близкий к используемому в эксперименте. Предложено динамическое уравнение для поперечного размера ячейки моделирования.
3. Проведено моделирование развития пластической деформации ГПУ кристаллов при одноосном растяжении. Показана принципиальная возможность имитации с помощью этого метода кривых растяжения совершенных кристаллов, изменения температуры образца, появления дислокаций, полос скольжения, одиночных вакансий и их скоплений, а также процесса разрушения кристаллов.
Список использованных источников
1. В.В.Кирсанов, ЭВМ-эксперимент в атомном материаловедении, Энергоатомиздат, 1990.
2. J.Schiotz, Scripta Mater., 51, 837 (2004).
3. K.W.Jacobsen, J.K.Norskov, M.J.Puska, Phys. Rev. B35, 7423 (1987).
4. K.W.Jacobsen, P.Stoltze, J.K.Norskov, Surf. Sci. 366, 394 (1996).
5. L.Verlet, Phys. Rev. 159, 98 (1967); Phys. Rev. 165, 201 (1967).
6. D. van der Spoel, E. Lindahl, B. Hess at al. Gromacs User Manual, v. 3.2, University of Groningen.
7. K. Refson. Moldy User’s Manual, v. 2.16, (2001).
8. W.Smith, M.Leslie, T.R.Forester. The DL_POLY_2 User Manual, (2003), Daresbery Laboratory.
9. J.B.Gibson, A.N.Goland, M.Milgram, G.H.Vineyard, Phys. Rev. 120, 1229 (1960).
10. M.P.Allen, D.J.Tildesley Computer simulation of liquids. Clarendon Press, Oxford, 1989.
11. K.Nordlund, Comput. Mater. Sci., 3, 448 (1995).
12. J.F.Ziegler, J.P.Biersack, U.Littmark, The stopping and range of ions in solids. Pergamon Press, N.Y., 1987.
13. J.Schiotz, T.Vegge, F. D. Di Tolla, K.W.Jacobsen, Phys. Rev. B60, 11971 (1999),cond-mat/9902165.
14. T.Egami, K.Maede, and V.Vitek, Phil. Mag. A 41, 883 (1980).
15. J.R.Ray and A.Rahman, J. Chem. Phys. 80, 4423 (1984).
16. H.Jonsson and H.C.Andersen, Phys. Rev. Lett. 60, 2295 (1988).
17. A.S. Clarke and H.Jonsson, Phys. Rev. E 47, 3975 (1993).
18. Р.Хоникомб Р. Пластическая деформация металлов. М. Мир. 1972.
19. И.М.Неклюдов, Н.В.Камышанченко. Физические основы прочности и пластичности металлов. ч. 3. Пластическая деформация и разрушение кристаллических материалов. Изд. “Педагогика-Пресс” и Белгородского государственного университета, Белгород, 2001
Похожие работы
... базе Института физики прочности и материаловедения СО РАН издается на русском и английском языках международный журнал «Физическая мезомеханика». 4. Моделирование как средство экспериментального исследования Моделирование всегда используется в комплексе с другими общенаучными и специальными методами. Теснее всего моделирование связано с экспериментом. Попробуем разобраться, в чем отличие ...
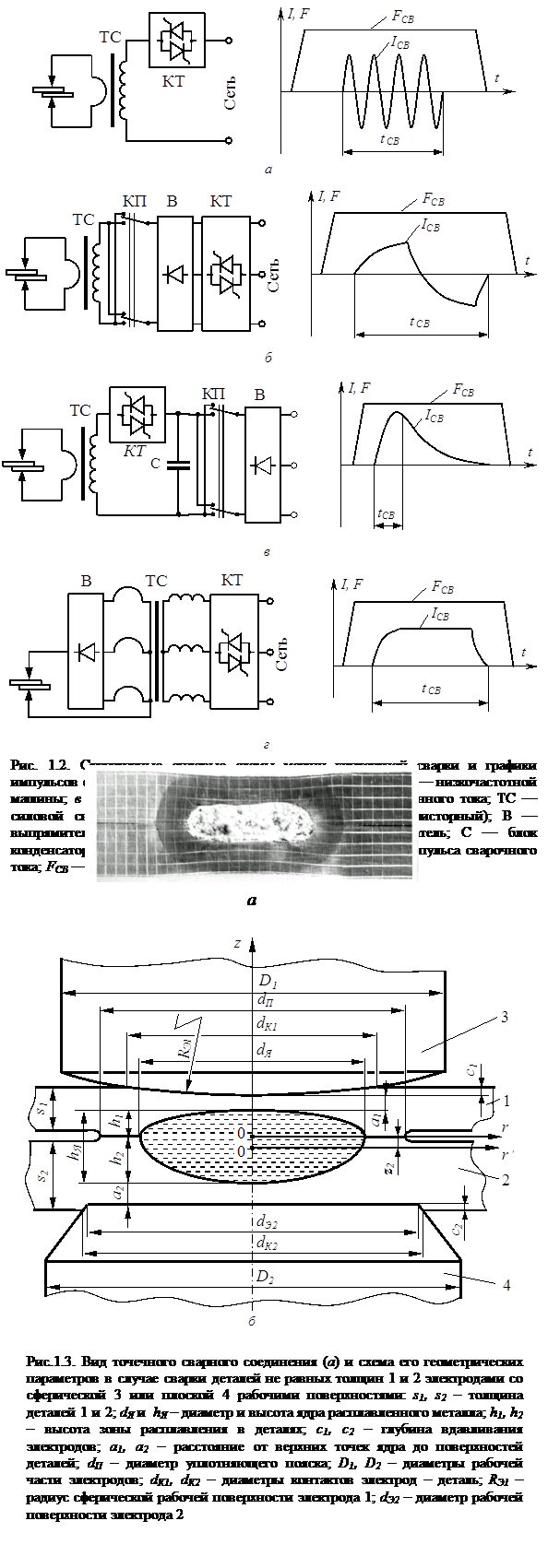
... , при обработке металлов давлением. Экспериментальные исследования процессов пластической деформации металла в зоне формирования соединения при контактной точечной сварке по этой методике проводятся на натурных образцах с предварительно нанесенной координатной сеткой, технология изготовления которых предложена и описана в работе [128]. При исследованиях пластических деформаций в плоскостях ...
... повысить пластичность поверхностных слоев на 40%. Это позволяет на 10-15% снизить энергозатраты на прокатку. Применение технологических смазок Применение традиционных смазочных материалов (минерального, растительного масла, синтетических смазок с содержанием поверхностно-активных веществ и др.) на толстолистовых станах трудно реализуемо из-за дефицитности и недостаточной эффективности, ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
0 комментариев