Навигация
Теорема об изменении момента количества движения
6852
знака
0
таблиц
6
изображений
3. Теорема об изменении момента количества движения
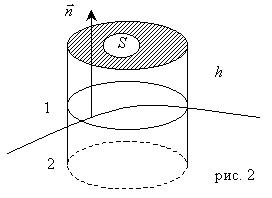
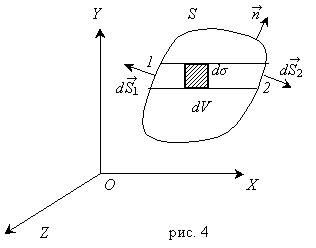
Будем предполагать, что момент количества движения для сплошной среды равен моменту вектора количества движения относительно какой-либо точки. Так, для части континуума, изображенной на рис. 2.1, полный момент количества движения относительно начала координат по определению равен интегралу
, или 
, (3.1)
где 
- радиус-вектор элемента объема dV. Теорема об изменении момента количества движения утверждает, что скорость изменения момента количества движения произвольно выбранной части континуума относительно любой точки равна главному моменту (относительно той же точки) массовых и поверхностных сил, действующих на рассматриваемую область среды. Для объема V сплошной среды можно написать уравнение момента количества движения в интегральной форме:
,
или (3.2)
Уравнение (3.2) справедливо для таких сред, в которых силы взаимодействия частиц равны по величине, коллинеарны и противоположны по направлению, а распределенные моменты отсутствуют. Уравнение момента количества движения не всегда представляет собой новое дифференциальное уравнение. Если в (3.2) подставить 
и предположить симметрию тензора напряжений, то уравнение будет удовлетворено тождественно при учете только соотношения (2.6). Если же симметрия тензора напряжений не предполагается заранее, то она получается как прямое следствие уравнения (3.2), которое после подстановки сводится к виду
, или 
(3.3)
В силу произвольности объема V это ведет к равенствам
, или 
, (3.4)
откуда видно, что 
.
ЗАДАНИЕ ДЛЯ РАСЧЕТНОЙ РАБОТЫ
По заданному в эйлеровых координатах закону распределения компонент тензора истинных напряжений, полагая плотность постоянной, определить:
1. Закон распределения массовых сил, при котором среда находится в равновесии.
2. Построить эпюры нормальных и касательных составляющих вектора напряжений на границе куба со сторонами 
.
3. Найти главный вектор поверхностных (определить нормальную и касательную составляющие) сил и массовых сил.
4. Найти главный момент поверхностных и массовых сил. Убедиться в их равновесии.
5. Полагая массовые силы отсутствующими, найти поле ускорений в эйлеровых координатах.
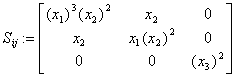
Выполнение расчетной работы
По заданному в эйлеровых координатах закону распределения компонент тензора истинных напряжений, полагая плотность постоянной, определить:
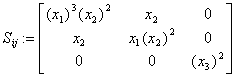
1. Определим закон распределения массовых сил, при котором среда находится в равновесии, для этого составим уравнение движения:
Условие равновесия: 
.
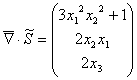
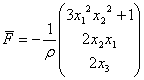
2. Построить эпюры нормальных и касательных составляющих вектора напряжений на границе куба со сторонами .
Построим нормальные составляющие.
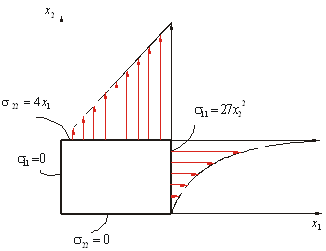
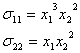
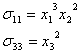
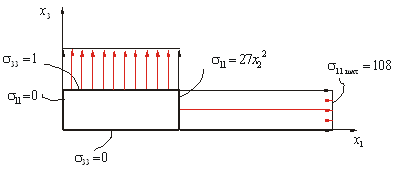
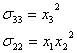
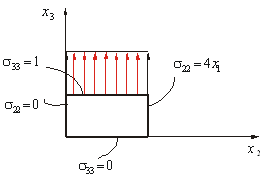
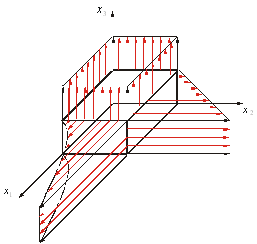
Построим касательные составляющие.
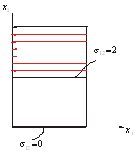
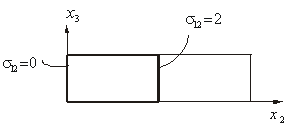
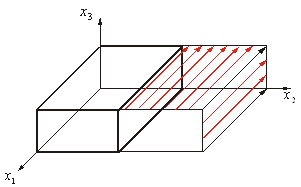
3. Найти главный вектор поверхностных (определить нормальную и касательную составляющие) сил и массовых сил.
Найдем главный вектор массовых сил: 
.
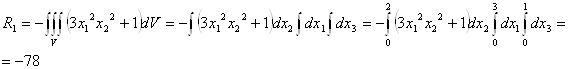
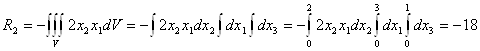
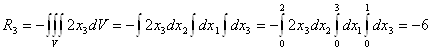
Найдем главный вектор поверхностных сил: 
.
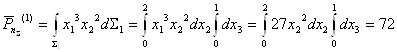
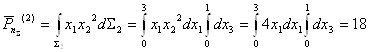
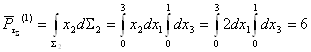
Т.к. 
, то система находится в равновесии.
4. Найти главный момент поверхностных и массовых сил. Убедиться в их равновесии.
Найдем главный момент поверхностных сил относительно центра заданного объема, т.е. параллепипида со сторонами 3x2x1.
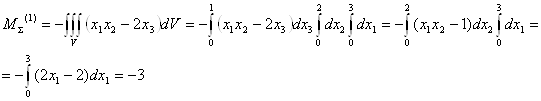
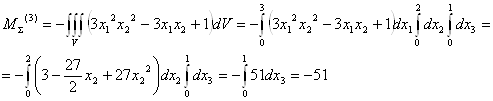
Найдем главный момент массовых сил:
Но 
, поэтому 
и условие равновесия автоматически выполняется.
5. Полагая массовые силы отсутствующими, найти поле ускорений в эйлеровых координатах.
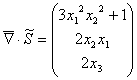
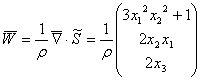
Похожие работы
... тензора внутренних напряжений в идеальной жидкости (газе) имеет вид: , (2.6) и тензор P целиком определяется скаляром p. Понятно, что идеальная жидкость не единственно возможная модель сплошной среды, позволяющая определить компоненты тензора внутренних напряжений. Можно, например, рассматривать его компоненты как функции от деформации частицы: в этом случае среда называется упругой. В ...
... состояние равновесия – на поверхность тела действует сила давления жидкости, которая уравновешивает вес жидкости внутри поверхности. Движение жидкостей и газов. Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время ...
... Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4). В случае стационарных электрических и магнитных полей ( и) система уравнений Максвелла (1) – (4) распадается на систему уравнений электростатики: , , ...
... как правило, не могут быть найдены теоретически, поэтому для оценок интенсивности и спектрального состава звука используют различные модели турбулентного движения[13,15]. 2.2 Краткая история акустики движущихся сред В науке сформировалось новое самостоятельное направление, получавшее название аэроакустики. Зародившаяся на стыке двух наук — аэродинамики и классической акустики, она связана с ...
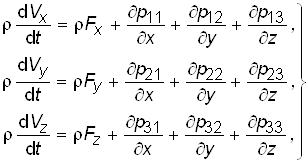
0 комментариев