Навигация
Определение ускорений точек A и B и угловое ускорение звена АВ
3. Определение ускорений точек A и B и угловое ускорение звена АВ.
Определяем ![]() и
и ![]() .
.
С помощью теоремы об ускорениях точек плоской фигуры определяем ускорение точки В:
![]() .
.
Т.к. кривошип О1А вращается равномерно, то ускорение точки А направлено к центру О1 и равно
![]() см/с2.
см/с2.
Центростремительное ускорение точки В во вращательном движении шатуна АВ вокруг полюса А направлено от точки В к точке А и равно
![]() 0,43=19,43 см/с2.
0,43=19,43 см/с2.
Откладываем от точки В в соответствующем масштабе ускорение полюса ![]() . Из конца вектора
. Из конца вектора ![]() строим вектор
строим вектор ![]() , проводя его параллельно ВА. Через конец вектора
, проводя его параллельно ВА. Через конец вектора ![]() проводим прямую JK, перпендикулярную ВА, т.е. параллельную вращательному ускорению
проводим прямую JK, перпендикулярную ВА, т.е. параллельную вращательному ускорению ![]() . Однако определить ускорение
. Однако определить ускорение ![]() этим построением невозможно, т.к. его направление неизвестно.
этим построением невозможно, т.к. его направление неизвестно.
Чтобы найти ускорение точки В, необходимо выполнить второе построение, рассматривая эту точку как принадлежащую О2В. В этом случае
![]()
Центростремительное ускорение точки В:
![]() см/с2.
см/с2.
Откладываем от точки В вектор ![]() , направив его к центру О2. Через конец вектора
, направив его к центру О2. Через конец вектора ![]() проводим прямую LN перпендикулярно О2В, т.е. параллельно вращательному ускорению
проводим прямую LN перпендикулярно О2В, т.е. параллельно вращательному ускорению ![]() .
.
Точка пересечения этой прямой с JK определяет концы векторов ![]()
![]() ,
, ![]()
Измерением на чертеже получаем
![]() 80 см/с2.
80 см/с2.
![]() 49 см/с2.
49 см/с2.
Т.к. ![]() =АВ
=АВ![]() , то угловое ускорение звена АВ
, то угловое ускорение звена АВ
![]()
![]() /АВ=49/45=1,09 рад/с2.
/АВ=49/45=1,09 рад/с2.
4)Определение положения мгновенного центра ускорений звена АВ.
Примем точку А за полюс. Тогда ускорение точки В
![]()
Строим параллелограмм ускорений при точке В по диагонали ![]() и стороне
и стороне ![]() . Сторона параллелограмма
. Сторона параллелограмма ![]() выражает ускорение точки В во вращении АВ вокруг полюса А. Ускорение
выражает ускорение точки В во вращении АВ вокруг полюса А. Ускорение ![]() составляет с отрезком АВ угол
составляет с отрезком АВ угол ![]() , который можно измерить на чертеже.
, который можно измерить на чертеже.
Направление вектора ![]() относительно полюса А позволяет определить направление
относительно полюса А позволяет определить направление ![]() , в данном случае соответствующее направлению часовой стрелки Отложив угол
, в данном случае соответствующее направлению часовой стрелки Отложив угол ![]() от векторов
от векторов ![]() и
и ![]() в этом направлении и проводя два луча, найдем точку их пересечения
в этом направлении и проводя два луча, найдем точку их пересечения ![]() - мгновенный центр ускорений звена АВ.
- мгновенный центр ускорений звена АВ.
5) Определение ускорения точки М.
Найдем ускорение точки М с помощью МЦУ.
Ускорения точек плоской фигуры пропорциональны их расстояниям до мгновенного центра ускорений:
![]() .
.
Подставив расстояния, определенные по чертежу
К7. Определение абсолютной скорости и абсолютного ускорения точки
![]()
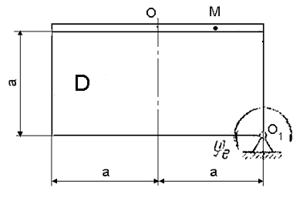 Дано:
Дано:
OM=Sr(t)=25sin(![]() t/3);
t/3);
![]()
![]() 4c
4c
![]() a=25см
a=25см
v-?
a-?
Положение точки М на теле D определяется расстоянием Sr=ОМ.
При ![]() 4c Sr=25 sin(
4c Sr=25 sin(![]() 4/3)= -21,65 см.
4/3)= -21,65 см.
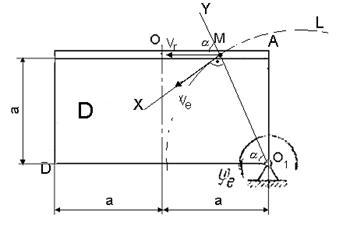
Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:
![]()
Модуль относительной скорости ![]()
![]() , где
, где ![]() dSr/dt=25cos(
dSr/dt=25cos(![]() t/3)
t/3) ![]() /3
/3
При t=4c ![]() -13,08см/с.
-13,08см/с.
![]() 13,08см/с.
13,08см/с.
Отрицательный знак у ![]() показывает, что вектор
показывает, что вектор![]() направлен в сторону убывания Sr.
направлен в сторону убывания Sr.
Модуль переносной скорости ![]() =
=![]() , где
, где
![]() -радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М,
-радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М,
![]() -модуль угловой скорости тела.
-модуль угловой скорости тела.
Найдем ![]() .
.
Рассмотрим прямоугольный треугольник ![]() .
.
АМ=ОА-ОМ.
АМ=25-21,65=3,35см.
![]() =25см.
=25см.
По теореме Пифагора имеем:
![]()
![]() =25,22см.
=25,22см.
Найдем ![]() .
.
![]() , где
, где ![]()
![]() =d
=d![]() /dt =4t-0,5
/dt =4t-0,5
При t=4c ![]()
![]() =15,5рад/с.
=15,5рад/с.
Знак ”+” у величины ![]() показывает, что вращение тела D происходит в ту же сторону, в которую ведется отсчет угла
показывает, что вращение тела D происходит в ту же сторону, в которую ведется отсчет угла ![]() .
.
Тогда модуль переносной скорости
![]() =
=![]() =390,91 см/с.
=390,91 см/с.
Модуль абсолютной скорости v найдем способом проекций.
Через точку М проводим оси X и Y.
![]()
![]()
![]()
![]()
Из треугольника ![]() :
:
![]() =AM/
=AM/![]()
![]() =3,35/25,22=0,13
=3,35/25,22=0,13
![]()
![]()
Тогда
![]()
![]() 1,704 см/с
1,704 см/с
![]() 403,86см/с.
403,86см/с.
Значит v = ![]()
![]() 403,86см/с.
403,86см/с.
Абсолютное ускорение точки М равно геометрической сумме относительного, переносного и кориолисова ускорений.
![]() , где в свою очередь
, где в свою очередь
![]()
![]()
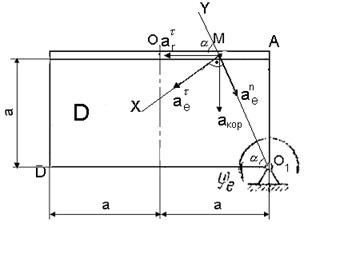
Относительное движение.
Это движение происходит по закону Sr(t)=25sin(![]() t/3);
t/3);
Модуль относительного касательного ускорения ![]() ,
,
где ![]() =d2Sr/dt=
=d2Sr/dt=![]()
При t=4c ![]() 23,72см/с2.
23,72см/с2.
![]() 23,72см/с2.
23,72см/с2.
Модуль относительного центростремительного ускорения ![]() =0, т.к. радиус кривизны относительной траектории стремится к бесконечности.
=0, т.к. радиус кривизны относительной траектории стремится к бесконечности.
Переносное движение.
Это движение происходит по закону
![]()
Модуль переносного вращательного ускорения ![]() , где
, где
![]() =
=![]() - модуль углового ускорения тела D
- модуль углового ускорения тела D
![]() d2
d2![]() /dt2=4рад/с2
/dt2=4рад/с2
Знаки у ![]() и
и ![]() одинаковые. Значит вращение тела D ускоренное.
одинаковые. Значит вращение тела D ускоренное.
Тогда ![]() см/с2
см/с2
Модуль переносного центростремительного ускорения
![]()
![]() =6059,1 см/с2.
=6059,1 см/с2.
Кориолисово ускорение.
Модуль кориолисова ускорения определяем по формуле
![]() , где
, где
![]() - угол между вектором
- угол между вектором ![]() и осью вращения (вектором
и осью вращения (вектором ![]() ).
).
В нашем случае ![]() =
=![]() , т.к. ось вращения перпендикулярна плоскости вращения тела D.
, т.к. ось вращения перпендикулярна плоскости вращения тела D.
Тогда ![]() 12118,21 см/с2.
12118,21 см/с2.
Направление вектора ![]() найдем по правилу Н.Е.Жуковского: т.к. вектор
найдем по правилу Н.Е.Жуковского: т.к. вектор ![]() лежит в плоскости, перпендикулярной оси вращения, то повернем его на
лежит в плоскости, перпендикулярной оси вращения, то повернем его на ![]() в направлении
в направлении ![]() , т.е. против хода часовой стрелки.
, т.е. против хода часовой стрелки.
Модуль абсолютной скорости v найдем способом проекций.
Через точку М проводим оси X и Y.
![]() +
+![]()
![]() =100,88+23,72
=100,88+23,72![]() -6059
-6059![]() =-663,3см/с2.
=-663,3см/с2.
![]()
![]() 18174,22см/с2.
18174,22см/с2.
![]()
![]() =18186,32см/с2.
=18186,32см/с2.
Ответ: ![]() 13,08см/с
13,08см/с ![]() =390,91 см/с.
=390,91 см/с. ![]() 403,86см/с.
403,86см/с.
![]() 23,72 см/с2,
23,72 см/с2, ![]()
![]() см/с2,
см/с2, ![]() =6059,1 см/с2,
=6059,1 см/с2, ![]() 12118,21 см/с2,
12118,21 см/с2, ![]() =18186,32
=18186,32
Похожие работы
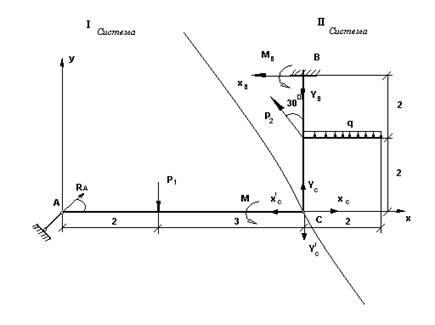
... (9) где RCx = R`Cx, RCy = R`Cy. Таким образом, имеем систему 4 уравнений (1), (2), (6) и (9) с 4 неизвестными. Из уравнения (9) Из уравнения (1) С-3. Определение реакций опор составной конструкции Из уравнения (6) Из уравнения (2) Найдем реакции шарнира С: RCx = -RBx = 12,5 кН, RCy = -RBy = 0,07 кН. Отрицательные значения RBx и RBy говорят о том, что ...
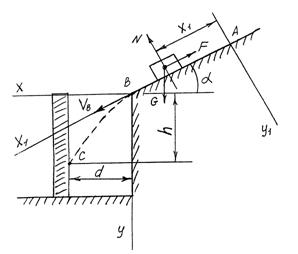
... a=15 cм/c Найти: , , a, a, , Решение: ОА=ОВ=14,1 см. =0,7= СP=см. = = см/с a=15 см/, т.к. ползуны двигаются по направляющим и совершают только поступательное движение. см/ см/ 9,85 см/ см/с Ответ: см/с см/с 9,85 см/ =15 см/ Статика твердого тела I. Плоская система сил система произвольно расположенных сил Определение реакций опор твердого тела ...
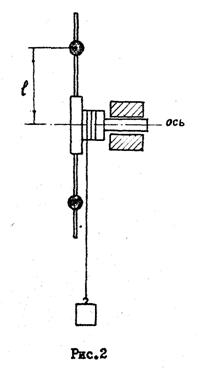
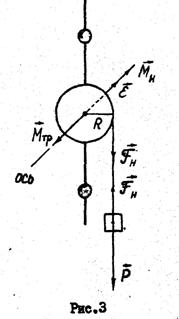
... ВПО «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет общих математических и естественнонаучных дисциплин Кафедра общей физики ЛАБОРАТОРНАЯ РАБОТА №23 Проверка основного закона динамики вращательного движения твердого тела относительно неподвижной оси выполнил: студент гр. 5СКб-11 Череповец, 2009/10 уч. Год проверил: ассис. Герасимов Р.А. Введение ...
... (3.2) Здесь L- момент импульса твердого тела относительно некоторой точки, - суммарный момент внешних сил относительно той же самой точки. К уравнениям (3.1) и (3.2), являющимся уравнениями динамики твердого тела, необходимо дать следующие комментарии: 1. Внутренние силы, как и в случае произвольной системы материальных точек, не- влияют на движение центра масс и не могут изменить ...



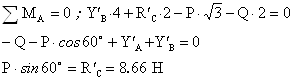
0 комментариев