Навигация
Метод, основанный на дескриптивных моделях
2.2 Метод, основанный на дескриптивных моделях
Параллельно с попытками оценить точки Лаффера методом, основанным на оптимизационных моделях, Балацким Е.В. [4] вводится принципиально новая применительно к теории налогов концептуальная линия, основанная на дескриптивной модели.
Методика анализа лафферовых эффектов с помощью дескриптивных моделей. Для простоты модельных построений ограничимся тремя видами налогов: на добавленную стоимость, прибыль и заработную плату. В этом случае общая масса налоговых сборов складывается из трех составляющих фискальных платежей: ![]() , где
, где ![]() - совокупные налоговые поступления,
- совокупные налоговые поступления, ![]() - фискальные поступления от налогов на добавленную стоимость, заработную плату и прибыль, соответственно.
- фискальные поступления от налогов на добавленную стоимость, заработную плату и прибыль, соответственно.
Чистую прибыль предприятия представим:
![]()
где ![]() - валовой общий продукт;
- валовой общий продукт; ![]() - материальные затраты (промежуточное потребление);
- материальные затраты (промежуточное потребление);![]() - затраты на заработную плату в текущих ценах (не включая налоги и социальные начисления);
- затраты на заработную плату в текущих ценах (не включая налоги и социальные начисления);![]() - амортизационные отчисления в текущих ценах;
- амортизационные отчисления в текущих ценах; ![]() - ставки налогов на прибыль, добавленную стоимость и заработную плату, соответственно.
- ставки налогов на прибыль, добавленную стоимость и заработную плату, соответственно.
Тогда суммарные налоговые сборы можно представить в виде:
![]() (6)
(6)
Предположим, что все рассматриваемые агрегаты ![]() и
и ![]() зависят от уровня цен
зависят от уровня цен ![]() . Введем следующие показатели эластичностей по цене:
. Введем следующие показатели эластичностей по цене: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и показатели производственной структуры затрат:
, и показатели производственной структуры затрат: ![]() ,
, ![]() ,
, ![]() . Продифференцируем уравнение (6) по
. Продифференцируем уравнение (6) по ![]() :
:
![]()
![]()
(помножим обе части на ![]() )
)
![]()
![]()
![]()
![]()
(разделим полученное равенство на ![]() )
)
![]()
Тогда уравнение (6) можно переписать в форме эластичностей с учетом сложившейся народнохозяйственной структуры затрат:
![]() (7)
(7)
Учитывая, что
![]()
![]()
т.е.
![]()
Тогда уравнение (7) можно записать в виде:
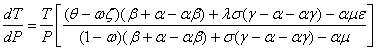 (8)
(8)
Выведенное дифференциальное уравнение (8) представляет собой дескриптивную модель формирования бюджетных доходов в инфляционной обстановке с учетом сложившейся производственной структуры затрат.
Введем в рассмотрение фискально-ценовый коэффициент ![]() :
:
![]()
Фискально-ценовый коэффициент определяет величину эластичности налоговых сборов по ценам. Если все параметры эластичности и структурные показатели затрат постоянны, то решением (8) является следующая степенная функция:
![]() (9)
(9)
где ![]() - постоянная интегрирования.
- постоянная интегрирования.
Так как одним из факторов, ведущих к росту налоговых сборов, в нашем случае являются цены, то в дальнейшем, во избежание проявления уже упомянутого эффекта Оливера-Танци, будем рассматривать реальные (дефлированные) налоговые поступления ![]() , которые очищены от инфляционной составляющей. Для рассматриваемой нами инфляционной среды такой подход является более корректным и содержательным. Поэтому вместо (9) будем использовать зависимость:
, которые очищены от инфляционной составляющей. Для рассматриваемой нами инфляционной среды такой подход является более корректным и содержательным. Поэтому вместо (9) будем использовать зависимость:
![]() (10)
(10)
Чтобы разобраться в специфике образования точек Лаффера, рассмотрим простейший случай, когда в зависимости (10) изменяется только один налоговый параметр (т.е. найдем автономную точку Лаффера). Для определенности пусть это ставка налога на добавленную стоимость. Для случая ![]() из (10) получим условие, при котором
из (10) получим условие, при котором ![]() .
.
![]()
![]()
![]()
![]() (11)
(11)
Если обозначить числитель и знаменатель дроби (11), как
![]()
![]()
тогда

Т.к. нас интересует ![]() , то опустим положительный знаменатель
, то опустим положительный знаменатель ![]()
![]()
![]()
![]()
т.к. ![]() (налог<100%), то
(налог<100%), то ![]() , тогда имеем
, тогда имеем
![]()
![]()
![]()
откуда, путем приведения подобных слагаемых, получим условие
![]() (12)
(12)
Аналогичная ситуация характерна и для ставки налога на прибыль. Для этого налога ![]() при условии
при условии
![]() (13)
(13)
Из (12) и (13) видно, что в стабильной ценовой среде классический эффект Лаффера на проявляется и, соответственно, точка Лаффера отсутствует. Однако ситуация в корне меняется, когда сдвиг налоговой ставки происходит на фоне ненулевой инфляции.
Чтобы определить совместное влияние роста цен и увеличения налоговой ставки (для определенности и наглядности ограничимся налогом на добавленную стоимость) необходимо рассмотреть поведение величины дифференциала ![]() :
:
![]() (14)
(14)
Введя обозначение темпа прироста цен ![]() , и учитывая, что
, и учитывая, что ![]() для случая
для случая ![]() , условие
, условие ![]() позволяет получить выражение для стационарной точки
позволяет получить выражение для стационарной точки ![]() :
:
![]()
![]()
![]()
Откуда
![]() (15)
(15)
Полученная формула (15), отличная от конструкции предлагаемой Балацким Е.В.:
![]() , (15')
, (15')
на наш взгляд, является единственно правильной.
Из (14) и (15) вытекает, что при ![]() ,
, ![]() и
и ![]()
![]() и точка
и точка ![]() - автономная точка Лаффера второго рода, т.к. при переходе через нее
- автономная точка Лаффера второго рода, т.к. при переходе через нее ![]() меняет знак с “+” на “-” .
меняет знак с “+” на “-” .
Проведем при помощи математического приложения “MathCAD 2001” апробацию полученной конструкции ссылаясь на показатели украинской экономики 1991-1994 гг.
Табл. 2.
Показатели для экономики России за 1991-1994 гг.
|
|
|
|
|
|
|
|
|
|
|
|
| 13,90% | 55,11% | 6,48% | 0,88 | 0,79 | 0,94 | 1,14 | 35,00% | 20,00% | 41,00% | 5,00% |
Для приведенных показателей все вышеприведенные условия верны: ![]() ,
, ![]() .
.
Единственной проблемой при проведении численного эксперимента стало определение величины уровня цен ![]() . Т.к. в формуле (15') у Балацкого уровень цен не фигурирует, статистические данные относительно данного показателя им не приводятся. В связи с информационной недостаточностью, показатель
. Т.к. в формуле (15') у Балацкого уровень цен не фигурирует, статистические данные относительно данного показателя им не приводятся. В связи с информационной недостаточностью, показатель ![]() был взят нами как переменная, такая что
был взят нами как переменная, такая что ![]() , т.е.
, т.е. ![]() . И, полагаясь на это, нами была построена функция (15) выражающая зависимость точки Лаффера от уровня цен
. И, полагаясь на это, нами была построена функция (15) выражающая зависимость точки Лаффера от уровня цен ![]() :
:

Полученная функция, как можно судить из графика, на отрезке ![]() принимает значения из области
принимает значения из области ![]() . Поэтому найденная нами точка Лаффера
. Поэтому найденная нами точка Лаффера ![]() .
.
Обсуждение метода. Одним из серьезных минусов дескриптивной модели является несоответствие априорным граничным условиям, указанным нами в пункте 1. Действительно,

![]()
ни одно из классических граничных условий ![]() и
и ![]() для дескриптивной модели (8) не выполняется, т.к. (9) генерирует ненулевые значения налоговых сборов на фискальных полюсах. Балацким Е.В., в отношении данного факта, делается предположение, что данная дескриптивная модель будет давать хорошие результаты только тогда, когда фискальные параметры находятся ближе к середине шкалы аргумента. При приближении параметров к своим границам метод, говорит он, может давать сильные погрешности. Если даже и принять на веру это сомнительное высказывание, то встает вопрос, где находиться эта середина и как оценить погрешности, возникаемые при оценке точек Лаффера? Ведь даже ошибка в 2-3% может привести государство к тяжелым социальным последствиям.
для дескриптивной модели (8) не выполняется, т.к. (9) генерирует ненулевые значения налоговых сборов на фискальных полюсах. Балацким Е.В., в отношении данного факта, делается предположение, что данная дескриптивная модель будет давать хорошие результаты только тогда, когда фискальные параметры находятся ближе к середине шкалы аргумента. При приближении параметров к своим границам метод, говорит он, может давать сильные погрешности. Если даже и принять на веру это сомнительное высказывание, то встает вопрос, где находиться эта середина и как оценить погрешности, возникаемые при оценке точек Лаффера? Ведь даже ошибка в 2-3% может привести государство к тяжелым социальным последствиям.
Также довольно сомнительно выглядит формула (15). Из нее следует, что необходимым условием существования точки Лаффера является ценовая нестабильность. Если же темп прироста цен ![]() , то любая установленная государством налоговая ставка будет оптимальной?
, то любая установленная государством налоговая ставка будет оптимальной?
Однако применение дескриптивных моделей в теории налогов очень молодой и не до конца изученный метод. И такие его свойства как макроэкономическая постановка модели, и ее внутренняя динамичность, из-за введения показателя инфляции, не позволили нам не затронуть данный метод в обзоре.
Похожие работы
... стабилизаторы не устраняют причин циклических колебаний равновесного ВНП вокруг его потенциального размера, а только ограничивают размах этих колебаний. Глава 2. Эффективность фискальной политики государства §2.1. Постановка проблемы и методология исследования. В последнее время проводится много исследований, в которых делается попытка оценить эффективность отдельных сторон фискальной ...
... те, которые предполагались в качестве первоначальных целей. По мнению большинства предпринимателей и экономистов, один из главных факторов, сдерживающих в России рост производственной активности, – нерациональная фискальная политика, проводимая государством на протяжении практически всех 90-х годов. Считается, что то налоговое бремя, которое установило государство, было явно чрезмерным и не ...
... -хозяйственной деятельности большая часть налоговых платежей поступает в бюджет РФ, что оказывает существенное влияние на Экономическое развитие РФ и на социальные программы, проводимые Правительством РФ. 2.2 Тенденции развития предпринимательской деятельности в РФ Специфика развития отечественного предпринимательства вызвана следующими причинами: - исторически быстрым и спонтанным ходом ...
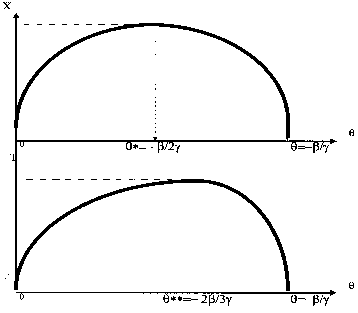
0 комментариев