Навигация
Применение эконометрического аппарата для оценки риска и доходности
3.1 Применение эконометрического аппарата для оценки риска и доходности.
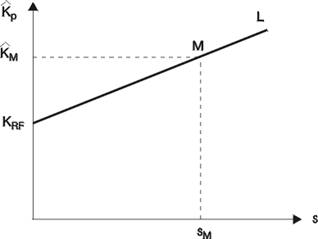
Какого-либо безусловного обещания хорошей доходности для спекулянта модель CAPM не дает: обещание может быть только условным, например, следующим: «если в течение будущего года среднерыночная плата за риск составит 5%, то математическое ожидание возврата актива, бета которого равна двум, будет равно 10% плюс безрисковый возврат». При этом замечается, что обычно большие значения «бета актива» связаны и с большой изменчивостью (волатильностью) цен данного актива, т.е. в конечном счете с большей вероятностью получить убыток при покупке именно этого актива. Речь о корреляциях случайных добавок для разных активов (т.е. о каком-то варианте эффективного портфеля) в CAPM не идет.
Приняв модель, мы действуем далее в соответствии с классическим регрессионным анализом: оцениваем коэффициент βi для каждого актива по данным о прошлых возвратах за какое-то количество периодов времени. Впрочем, некоторые учебники рекомендуют брать в качестве оценки βi величину cov(ri,rm)/Drm .(Конечно, имеется в виду, что ковариация и дисперсия заменяются их выборочными аналогами.) Многие авторы считают, что она ошибочна по следующим причинам. Во-первых, классический регрессионный анализ в случае модели без свободного члена, т.е. вида
Y = βX + E (E обозначает ошибку),
рекомендует несколько иную оценку, а именно
(Σxiyi)/ (Σxi2), (1)
которая более эффективна, чем критикуемая рекомендация. (По той простой причине, что (Σxi2) всегда больше, чем выборочная дисперсия xi, причем – особенно в эконометрике – разница может быть значительной.) Во- вторых, рекомендуемая оценка вообще верна лишь в том предположении, что в наблюдениях за все периоды безрисковый возврат rf остается постоянным. (В противном случае надо брать ковариации не самих возвратов, а их разностей с безрисковым возвратом.)
С точки зрения того опыта, который имеется в области применений регрессионного анализа, совершенно ясно, что требуется экспериментальная проверка эффективности любой модели, в частности и CAPM. В сложившемся эконометрическом подходе плохо еще и то, что такие проверки направляются на свойства остаточного члена в уравнениях модели (который изображает случайную ошибку). Возникают различные альтернативные гипотезы типа гетероскедастичности и/или зависимости остатков, которые определенным образом тестируются. Эконометрист видит окончательное счастье в том, чтобы модель прошла определенный набор тестов. Но следовало бы знать, что из истории обработки наблюдений в физическом и техническом эксперименте однозначно следует, что вероятностные предположения о модели остатков никогда не бывают выполнены. (Это, конечно, значит, что и те доверительные интервалы для параметров, которые принято вычислять, не заслуживают особого доверия.)
В случае модели CAPM применения мыслятся как довольно слабые: ведь все связывается с неизвестным будущим поведением среднерыночного возврата. Но все-таки и это представляет определенный если не практический, то научный интерес: хотя бы сама законность понятия «беты актива». Следовательно, необходимо проверить, во-первых, действительно ли в разные периоды времени можно для фиксированного актива говорить о примерно постоянном значении «бета». Во-вторых, следует оценить эффективность того условного (при условии, что будущее поведение рыночного индекса известно) предсказания будущих возвратов актива, которое вытекает из модели.
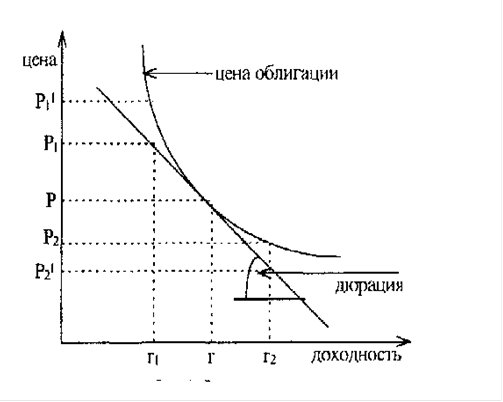
Изменчивость цен актива характеризуется параметром, который называется волатильностью. Вероятностное определение волатильности заключается в следующем. Предполагается, что динамика рыночных цен актива St обладает тем свойством, что математическое ожидание квадрата логарифмического приращения цены за время h примерно пропорционально h. Иными словами, постулируется соотношение
E(ln St+h - lnSt)2 = σ2h. (2)
(Конечно, имеется в виду, что значение приращения времени h не слишком малое и не слишком большое: ориентировочно в пределах от десятков минут до десятков дней.) Параметр σ в соотношении (2) и называется волатильностью. Теоретически он считается постоянным для фиксированного актива. На самом деле он несколько колеблется, но все-таки является достаточно серьезным параметром. Различные активы (например, акции различных компаний) могут иметь различающиеся (в два и более раз) волатильности, при этом (как правило) если волатильность одного актива значительно больше волатильности другого при оценке по одному интервалу времени, то это различие сохраняется и для других интервалов времени. (Понятно, что волатильность оценивается как среднее значение квадрата логарифмического приращения цены при каком-то фиксированном небольшом значении h, например, h=1 день. Но установилась неудачная традиция, согласно которой эта оценка пересчитывается на значение h=1 год, в то время как для таких больших интервалов времени динамика рыночных цен вообще не может рассматриваться как чисто случайная, т.е. неясен смысл математического ожидания в левой части соотношения (2).) Поскольку понятие волатильности, несомненно, имеет довольно точный смысл, вполне желательно его сопоставление с другими параметрами, в частности, с «бета актива». [5]
Похожие работы
... в помещении соответствуют общепринятым нормам, работающему обеспечены комфорт и благоприятные условия труда. Заключение В данном дипломном проекте произведено формирование портфеля ценных бумаг акционерного коммерческого банка «Дорожник». Процесс формирования и оптимизации включал в себя следующие этапы: Исследован теоретический материал по инвестиционному процессу, ценным бумагам и портфелю ...
... как в длительной перспективе плюсы и минусы от изменения их цены будут гасить друг друга. 4. Особенности практики управления портфелями ценных бумаг в России Российскому рынку по-прежнему характерны негативные особенности, препятствующие применению принципов портфельного инвестирования, что в определенной степени сдерживает интерес субъектов рынка к этим вопросам. В дополнение к уже описанным ...
... и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала. Мы не будем останавливаться подробно на математической интерпретации данной модели, однако отметим, что Марковитц разработал очень важное для современной теории портфеля ценных бумаг положение, которое гласит: совокупный риск портфеля можно разложить на две составные части. Первая - это систематический риск, ...
... для нее рисков, и предопределило цель и задачи данной работы. Целью диссертационной работы является разработка двухкритериальных целочисленных моделей и методов управления портфельными инвестициями, учитывающих требования по повышению доходности и снижению рыночных рисков финансовых инвестиций и ограничения реального сектора экономики при инвестициях в производственные запасы. Для достижения ...
0 комментариев