Навигация
Метод эквивалентных фильтрационных сопротивлений
35979
знаков
0
таблиц
19
изображений
2.1.7 Метод эквивалентных фильтрационных сопротивлений
Данный метод называется методом Борисова и позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки - к одиночно работающей скважине и к одиночно работающей батареи. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простейший физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (4.35) или (4.36) с законом Ома I=U / R, где I - ток, U - разность потенциалов и R - сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (4.35), который состоит из двух слагаемых. Если в (4.35) оставить только первое слагаемое, то оно будет выражать дебит в прямолинейно-параллельном потоке через площадь величиной nhs на длине L . Т.о. первое слагаемое выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Борисов назвал эту часть фильтрационного сопротивления - внешним фильтрационным сопротивлением
.(4.37)
Оставим теперь в (4.35) только второе слагаемое. В этом случае получим аналог формулы Дюпюи для суммарного дебита n скважин при плоскорадиальном течении и в предположении, что каждая скважина окружена контуром питания длиной s. Т.о. второе слагаемое выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин, и по Борисову оно получило название внутреннего
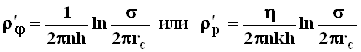.(4.38)
На внешнее и внутреннее фильтрационные сопротивления разделяется также полное фильтрационное сопротивление кольцевой батареи
.(4.39)
Здесь r выражает фильтрационное сопротивление потоку от контура питания к кольцевой батареи радиуса а в предположении, что поток плоскорадиален и батарея заменена галереей. Внутреннее сопротивление r/ - это сопротивление плоскорадиального потока от воображаемого контура окружности длиной 2pа/n к скважине. Величина 2pа/n - длина дуги сектора радиуса а, который содержит одну из скважин батареи.
Электрическая схема в случае одной батареи (рис.4.12) имеет вид (рис.4.13). На рис.4.12 затемнены области внутреннего сопротивления.
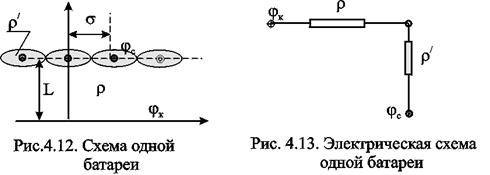
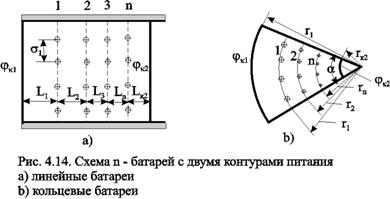
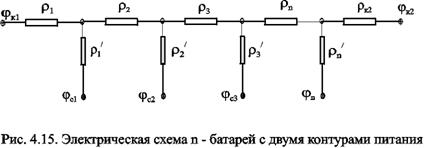
Рассмотрим случай притока к n эксплуатационным и нагнетательным батареям скважин и составим схему сопротивлений. Предположим, что скважины i-ой батареи имеют забойные потенциалы jсi (i=1,...,n), пласт имеет контурные потенциалы jк1 и jк2 (рис. 4.14). Пусть jк1 > jк2. Очевидно, поток от контура питания к первому ряду скважин будет частично перехватываться первой батареей и частично двигаться ко второй. Поток ко второй батарее будет частично перехватываться второй батареей, частично двигаться к третьей и т.д. Этому движению отвечает разветвленная схема фильтрационных сопротивлений (рис. 4.15).
Расчет ведется от контура с большим потенциалом к контуру с меньшим потенциалом, а сопротивления рассчитываются по зависимостям:
прямолинейная батарея
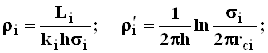(4.40)
круговая батарея
(4.41)
где Li - расстояние между батареями (для i=1 - L1=Lк1 ); ri - радиусы батарей (для i=1 - r0=rк ); ki - число скважин в батареи.
Дальнейший расчет ведется, как для электрических разветвленных цепей, согласно законам Ома и Кирхгоффа:
- алгебраическая, сумма сходящихся, в узле дебитов равна нулю, если считать подходящие к узлу дебиты положительными и отходящие - отрицательными.
алгебраическая сумма произведения дебитов на сопротивления (включая и внутреннее) равна алгебраической сумме потенциалов, действующих в замкнутом контуре. При этом и дебиты и потенциалы, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а направленное навстречу обходу отрицательным.
Следует помнить, что для последовательных сопротивлений r=Sri , а для параллельных
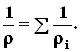
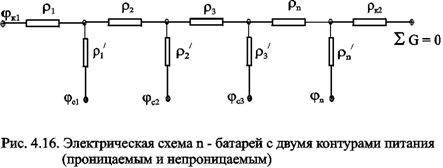
Если одна из границ непроницаема, то расход через неё равен нулю. В этом случае в соответствующем узле схемы фильтрационных сопротивлений задаётся не потенциал, а расход. На рис. 4.16 показана схема в случае непроницаемости второго контура. Вместо потенциала jк2, показанного на рис.4.15, здесь в узле задано условие SGi=0.
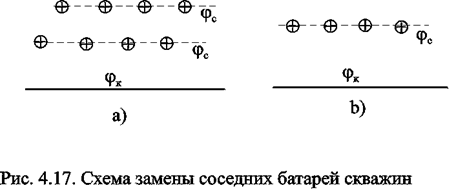
Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами. Если расстояние между скважинами много больше расстояния между батареями, то расчет надо вести по общим формулам интерференции скважин или использовать другие виды схематизации течения, например, заменить две близко расположенные соседние батареи скважин с редкими расстояниями между скважинами (рис. 4.17а) эквивалентной одной батареей - с суммарным числом скважин и проведенной посредине (рис.4.17b).
Вывод
В данной курсовой работе мы выведи дифференциальное уравнение движения сжимаемой и несжимаемой жидкости в пористой среде, то есть уравнение Лапласа. А так же рассмотрели плоские задачи теории фильтрации об установившемся притоке к скважине, такие как приток к совершенной скважине, фильтрационный поток от нагнетательной скважины к эксплуатационной, приток к группе скважин с удаленным контуром питания, приток к скважине в пласте с прямолинейным контуром питания, приток к скважине, расположенной вблизи непроницаемой прямолинейной границы, приток к скважине в пласте с произвольным контуром питания, приток к бесконечным цепочкам и кольцевым батареям скважин, приток к скважинам кольцевой батареи, приток к прямолинейной батареи скважин, метод эквивалентных фильтрационных сопротивлении.
Литература
1. Басниев В.С. и др. Подземная гидравлика. // М.:Недра,1986.-300с.
2. Евдокимова В.А., Кочина И.Н. Сборник задач по пдземной гидравлике. // М.:Недра.-166с.
3.Пыхачев Г.Б., Исаев Р.Г. Подземная гидравлика. //М:Недра,1973.- 359с.
4. Чарный И.А. Подземная гидрогазодинамика. // М. Изд.-во. Нефтяной и горно-топливной лит-ры.- 396с.
5. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. // М. Недра, 1984.- 211с.
Похожие работы
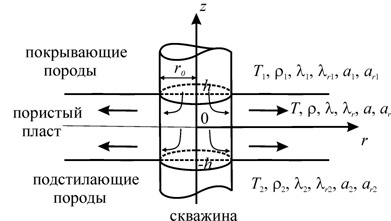
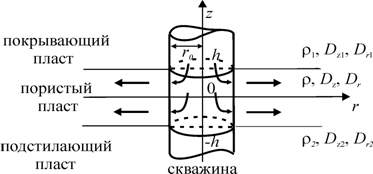
... влияния – RТ и чистой воды – Rwдля некоторого момента времени 3.6. Выводы В нулевом и первом приближениях решена задача о температурном поле, вызванном закачкой радиоактивного раствора в глубокозалегающие пласты. На основании полученного решения установлены расчетные формулы для полей температуры, вызванных энергией распада и различием температур пласта и закачиваемой жидкости. ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
... Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181) ...
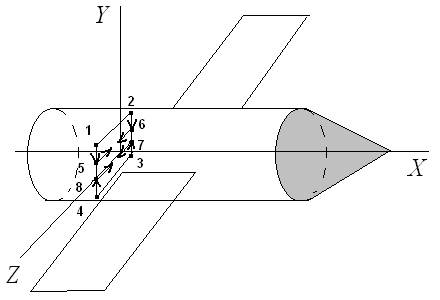
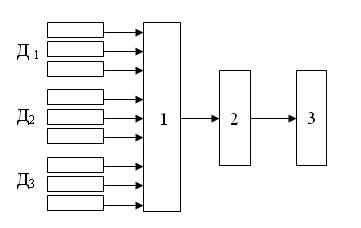
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
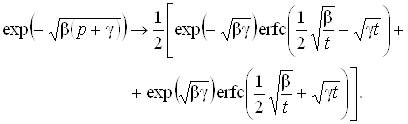
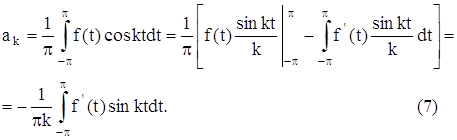
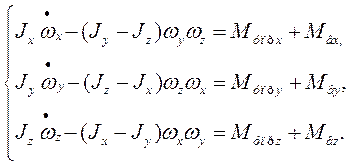
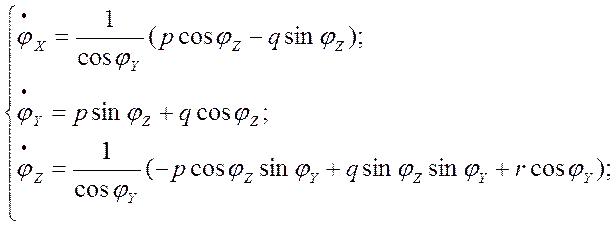
0 комментариев