Навигация
Ряды Фурье и их приложения
44324
знака
0
таблиц
22
изображения
Министерство общего и профессионального образования
Сочинский государственный университет туризма
и курортного дела
Педагогический институт
Математический факультет
Кафедра общей математики
ДИПЛОМНАЯ РАБОТА
Ряды Фурье и их приложения
В математической физике.
Выполнила: студентка 5-го курса
подпись дневной формы обучения
Специальность 010100
„Математика”
Касперовой Н.С.
Студенческий билет № 95471
Научный руководитель: доцент, канд.
подпись техн. наук
Позин П.А.
Сочи, 2000 г.
Содержание:
1. Введение.
2. Понятие ряда Фурье.
2.1. Определение коэффициентов ряда Фурье.
2.2. Интегралы от периодических функций.
3. Признаки сходимости рядов Фурье.
3.1. Примеры разложения функций в ряды Фурье.
4. Замечание о разложении периодической функции в ряд Фурье
5. Ряды Фурье для четных и нечетных функций.
6. Ряды Фурье для функций с периодом 2 l.
7. Разложение в ряд Фурье непериодической функции.
Введение.
Жан Батист Жозеф Фурье - французский математик, член Парижской Академии Наук (1817).
Первые труды Фурье относятся к алгебре. Уже в лекциях 1796 он изложил теорему о числе действительных корней алгебраического уравнения, лежащих между данными границами (опубл. 1820), названную его именем; полное решение о числе действительных корней алгебраического уравнения было получено в 1829 Ж.Ш.Ф. Штурмом. В 1818 Фурье исследовал вопрос об условиях применимости разработанного Ньютоном метода численного решения уравнений, не зная об аналогичных результатах, полученных в 1768 французским математиком Ж.Р. Мурайлем. Итогом работ Фурье по численным методам решения уравнений является «Анализ определённых уравнений», изданный посмертно в 1831.
Основной областью занятий Фурье была математическая физика. В 1807 и 1811 он представил Парижской Академии Наук свои первые открытия по теории распространении тепла в твёрдом теле, а в 1822 опубликовал известную работу «Аналитическая теория теплоты», сыгравшую большую роль в последующей истории математики. Это – математическая теория теплопроводности. В силу общности метода эта книга стала источником всех современных методов математической физики. В этой работе Фурье вывел дифференциальное уравнение теплопроводности и развил идеи, в самых общих чертах намеченные ранее Д. Бернулли, разработал для решения уравнения теплопроводности при тех или иных заданных граничных условиях метод разделения переменных (метод Фурье), который он применял к ряду частных случаев (куб, цилиндр и др.). В основе этого метода лежит представление функций тригонометрическими рядами Фурье.
Ряды Фурье теперь стали хорошо разработанным средством в теории уравнений в частных производных при решении граничных задач.
1. Понятие ряда Фурье. (стр. 94, Уваренков)
Ряды Фурье играют большую роль в математической физике, теории упругости, электротехнике и особенно их частный случай – тригонометрические ряды Фурье.
Тригонометрическим рядом называют ряд вида
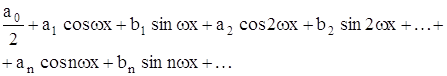
или, символической записи:
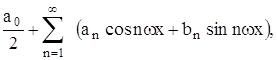( 1 )
где ω, a0, a1, …, an, …, b0, b1, …,bn, …- постоянные числа (ω>0) .
К изучению таких рядов исторически привели некоторые задачи физики, например задача о колебаниях
струны (XVIII в.), задача о закономерностях в явлениях теплопроводности и др. В приложениях рассмотрение тригонометрических рядов, прежде всего связано с задачей представления данного движения, описанного уравнением у = ƒ(χ), в
виде суммы простейших гармонических колебаний, часто взятых в бесконечно большом числе, т. е. в качестве суммы ряда вида (1).
Таким образом, мы приходим к следующей задаче: выяснить существует ли для данной функции ƒ(x) на заданном промежутке такой ряд (1),который сходился бы на этом промежутке к данной функции. Если это возможно, то говорят, что на этом промежутке функция ƒ(x) разлагается в тригонометрический ряд.
Ряд (1) сходится в некоторой точке х0, в силу периодичности функций 
(n=1,2,..), он окажется сходящимся и во всех точках вида 
(m- любое целое число), и тем самым его сумма S(x) будет (в области сходимости ряда) периодической функцией: если Sn(x) – n-я частичная сумма этого ряда, то имеем
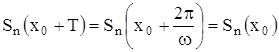
а потому и 
, т. е. S(x0+T)=S(x0). Поэтому, говоря о разложении некоторой функции ƒ(x) в ряд вида (1), будем предполагать ƒ(x) периодической функцией.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... Таким образом, имеется следующая задача : На основе существующих алгоритмов проанализировать возможность их применения как к последовательной обработке сигналов в реальном времени, так и к блочной обработке и оценить качество получаемых результатов . Критериями «качества» оценки спектральной плотности мощности в общем случае являются смещение этой оценки и ее дисперсия. Однако аналитическое ...
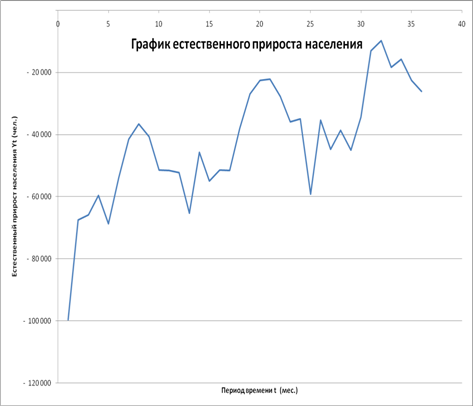
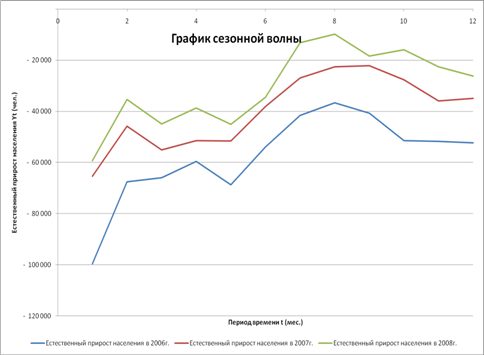
... , можно сделать вывод о том, что показатель естественного прироста населения наиболее точно прогнозируется рядом Фурье. Заключение В ходе работы было проведено моделирование и прогнозирование естественного прироста населения в РФ. Исследование было проведено с помощью следующих моделей: · Аддитивная модель; · Мультипликативная модель; · Одномерный анализ Фурье; · Регрессионная модель с ...
0 комментариев