Визначення норми річного стоку при наявності достатньої кількості даних спостережень

2. Визначення норми річного стоку при наявності достатньої кількості даних спостережень

Завдання 1 . характеристика басейну річки та гідрографічної мережі

Наводиться гідрографічна характеристика басейну річки.

Довжина l_гол головної річки Тетерів становить 247 км, довжина р. Уж – 27 км, р. Случ – 21 км. Річки Уж і Случ є притоками першого порядку.

Площа водозбірного басейну становить 10947 км².

Коефіцієнт звивистості k_зв визначаємо за формулою:

Довжина водозбірного басейну L становить 27 км. За формулою визначаємо середню ширину басейну:

км

Розраховуємо протяжність річкової системи:

247+27+21=295 км

Коефіцієнт щільності річкової мережі d розраховується за формулою:

d = 295/10947=0,03 км/км².

Коефіцієнт нерівномірності розвитку річкової мережі k_нер розраховується за формулою:

Визначити середнє багаторічне значення (норму) річного стоку при наявності даних спостережень.

Дано: середні річні витрати води р. Тетерів за період 1967-2000 рр. (всього за 34 роки).

Розв’язок: розрахунки статистичних параметрів річного стоку проводимо у вигляді таблиці.

У гр. 4 значення річного стоку розташовуємо у порядку зменшення.

Таблиця

№	Роки	Qi, м3/с	Qi, м3/с у ранжованому ряді	ki=Qi/Q0	ki-1	(ki-1)2	(ki-1)3	lgki	ki*lgki	P=(m/(n+1)) *100%
1	2	3	4	5	6	7	8	9	10	11
1	1967	0,81	6,53	3,023	2,023	4,0925	8,2792	0,480	1,452	2,857
2	1968	1,92	5,87	2,718	1,718	2,9515	5,0707	0,434	1,180	5,714
3	1969	2,28	3,52	1,63	0,630	0,3969	0,2500	0,212	0,346	8,571
4	1970	2,29	3,49	1,616	0,616	0,3795	0,2337	0,208	0,337	11,429
5	1971	2,28	3,32	1,537	0,537	0,2884	0,1549	0,187	0,287	14,286
6	1972	1,45	3,15	1,458	0,458	0,2098	0,0961	0,164	0,239	20
7	1973	3,49	3,09	1,43	0,430	0,1849	0,0795	0,155	0,222	22,857
8	1974	0,65	3,04	1,407	0,407	0,1656	0,0674	0,148	0,209	28,571
9	1975	1,65	2,43	1,125	0,125	0,0156	0,0020	0,051	0,058	31,429
10	1976	0,41	2,29	1,06	0,060	0,0036	0,0002	0,025	0,027	37,143
11	1977	3,15	2,28	1,056	0,056	0,0031	0,0002	0,024	0,025	40
12	1978	1,75	2,28	1,056	0,056	0,0031	0,0002	0,024	0,025	45,714
13	1979	3,32	2,25	1,042	0,042	0,0018	0,0001	0,018	0,019	48,571
14	1980	3,09	2,22	1,028	0,028	0,0008	0,0000	0,012	0,012	51,429
15	1981	0,69	2,14	0,991	-0,009	0,0001	0,0000	-0,004	-0,004	54,286
16	1982	0,63	2,12	0,981	-0,019	0,0004	0,0000	-0,008	-0,008	57,143
17	1983	1,08	1,98	0,917	-0,083	0,0069	-0,0006	-0,038	-0,035	60
18	1984	1,83	1,92	0,889	-0,111	0,0123	-0,0014	-0,051	-0,045	62,857
19	1985	1,52	1,83	0,847	-0,153	0,0234	-0,0036	-0,072	-0,061	65,714
20	1986	5,87	1,75	0,81	-0,190	0,0361	-0,0069	-0,092	-0,074	68,571
21	1987	6,53	1,75	0,81	-0,190	0,0361	-0,0069	-0,092	-0,074	71,429
22	1988	3,52	1,65	0,764	-0,236	0,0557	-0,0131	-0,117	-0,089	74,286
23	1989	1,41	1,52	0,704	-0,296	0,0876	-0,0259	-0,152	-0,107	77,143
24	1990	1,75	1,47	0,681	-0,319	0,1018	-0,0325	-0,167	-0,114	80
25	1991	1,16	1,45	0,671	-0,329	0,1082	-0,0356	-0,173	-0,116	82,857
26	1992	1,47	1,41	0,653	-0,347	0,1204	-0,0418	-0,185	-0,121	85,714
27	1993	1,38	1,38	0,639	-0,361	0,1303	-0,0470	-0,194	-0,124	88,571
28	1994	2,25	1,16	0,537	-0,463	0,2144	-0,0993	-0,270	-0,145	91,429
29	1995	2,12	1,08	0,5	-0,500	0,2500	-0,1250	-0,301	-0,151	94,286
30	1996	1,98	0,81	0,375	-0,625	0,3906	-0,2441	-0,426	-0,160	97,143
31	1997	2,43	0,69	0,319	-0,681	0,4638	-0,3158	-0,496	-0,158	97,234
32	1998	2,22	0,65	0,301	-0,699	0,4886	-0,3415	-0,521	-0,157	98,124
33	1999	3,04	0,63	0,292	-0,708	0,5013	-0,3549	-0,535	-0,156	98,231
34	2000	2,14	0,41	0,19	-0,810	0,6561	-0,5314	-0,721	-0,137	98,654
Сума		73,56	73,56		0,000	12,3812	12,0069	-2,473	2,400	-

Середню багаторічну величину стоку розраховуємо за формулою:

 м³/с

Перевірка розрахунків – сума модульних коефіцієнтів дорівнює кількості років спостережень:

Σk_i=34,056; Σ(k_i-1)=0 (допустима нев’язка – 0,05)

Виразити отриману у вигляді середньої багаторічної витрати води норму стоку через інші характеристики стоку: об’єму, модуль, шар та коефіцієнт стоку.

Дано: норма річного стоку р. Тетерів Q₀=2,16 м³/с, площа водозбору F=10947 км², середньо багаторічна норма річних опадів х₀=20117,7/34=591,7 мм.

Розв'язок: норму стоку виражаємо у інших одиницях стоку за формулами:

W=Q₀*T=2,6*31,56*10⁶=82,056 млн. м³ (у році 31,56*10⁶ с),

M=Q₀/F*10³=2,16/10947*10³=1,93 л/(с*км²),

y=h=W/F*10³=82,056/10947*10³=750 мм

коефіцієнт стоку розраховуємо за формулою:

α=h/x₀=750/591,7=1,3

Визначити коефіцієнт мінливості (варіації) річного стоку.

Дано: дані табл..

Розв'язок:

За методом найбільшої правдоподібності коефіцієнт варіації розраховуємо залежно від статистик λ₂ та λ₃:

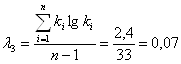
За номограмою знаходимо:

С_V=0,6; С_S=2С_V=2*0,6=1,2.

За методом моментів коефіцієнт варіації обчислюємо за формулою:

.

Визначити відносні середні квадратичні похибки норми стоку і коефіцієнта варіації.

Дано:

С_V=0,6

Розв'язок: величину відносної середньоквадратичної похибки σ_Q0розраховуємо за формулою:

Величину відносної середньоквадратичної похибки коефіцієнта варіації δС_V визначаємо за формулою:

%

%

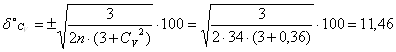Завдання 3. Побудова кривих забезпеченості річного стоку

Забезпеченістю гідрологічної характеристики називають імовірність перевищення розглядуваного значення цієї характеристики над усіма можливими її значенями. Наприклад, якщо середньорічна витрата води у 20 м³/с має забезпеченість 80%, то це означає, що у 80 випадках із 100 спостерігатиметься річна витрата, що дорівнюватиме 20 м³/с або більше.

Криву забезпеченості, побудовану за даними спостережень, називають емпіричною. Для її побудови хронологічний ряд річних витрат води Q₁, Q₂, Q_n систематизують у ранжований ряд (розташовують у порядку зменшення від найбільшого значення до найменшого) і обчислюють забезпеченість Р кожного члена ряду за формулою

Де m – порядковий номер члена ранжованого ряду; n – кількість членів ряду, тобто кількість років спостережень.

Отримані значення Р наносять на сітківку ймовірностей (тип сітківки залежить від співвідношення С_S/С_V) і проводять влавну усереднюючи криву емпіричну криву забезпеченості.

Для згладжування (вирівнювання) та екстраполяції (продовження) емпіричних кривих застосовують теоретичні (аналітичні) криві забезпеченості. Як правило, застосовується аналітична крива три параметричного гама-розподілу при будь-якому співвідношенні С_S/С_V та біноміальна крива розподілу при С_S>2С_V.

Для побудови аналітичної кривої три параметричного гама-розподілу ординати її знаходять за таблицею залежно від співвідношення С_S/С_V; потім за значенням С_V виписують модульні коефіцієнти К_Р%, які відповідають заданій забезпеченості. Для підвищення точності ординат кривої потрібно враховувати соті частки значення С_V (з точністю до двох знаків після коми) шляхом інтерполяції між суміжними колонками цифр.

Ординати біноміальної кривої знаходять за виразом:

К_Р%=Ф_Р%*С_V+1,

Де Ф_Р% - нормоване відхилення ординати кривої забезпеченості від середнього значення (при К_Р%=1), яке знаходять за таблицею.

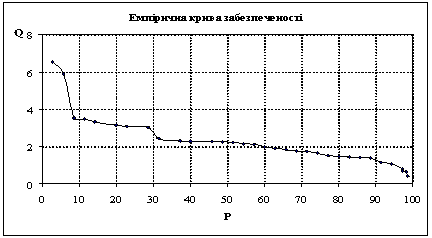
Побудувати емпіричну криву забезпеченості річного стоку.

Дано: середні річні витрати води Q_i р.Тетерів за період 1967-1991 рр.

Розвязок: для розрахунку забезпеченості Р значення річного стоку Q_i систематизує у ранжований ряд – розташовуємо у порядку зменшення. Координати емпіричної кривої забезпеченості (Р) обчислюємо за формулою:

Результати обчислень наведено у таблиці, гр..11. за цими даними на сітківку ймовірностей наносимо точки емпіричної кривої. По вісі абсцис відкладаємо забезпеченість (масштаб: 1 см – 5%), по вісі ординат – К_Р%. Для спрощення графік будуємо на міліметровому папері.

Побудувати теоретичну криву три параметричного гама-розподіу забезпеченості річного стоку.

Дано: коефіцієнт варіації С_V=0,6.

Розв'язок: координати теоретичних кривих три параметричного гама розподілу визначаємо за додатком для коефіцієнта асиметрії

С_S=1,5С_V, С_S=2С_V, С_S=2,5С_V

Записуємо їх у таблицю.

Отримані координати теоретичних кривих наносимо на сітківку ймовірностей. Спів ставляючи побудовані теоретичні криві з емпіричною кривою забезпеченості встановлюємо, що крива три параметричного гама розподілу при С_S=2,5С_V найкраще узгоджується з емпіричною, тому її приймаємо за розрахункову.

Таблиця Координати кривої забезпеченості три параметричного гама-розподілу середньорічних витрат води р. Тетерів

Забезпеченість
Р %	0,1	1	5	10	25	50	75	80	95	97	99
Ординати кривої
СS=1,5СV
КР%	3,02	2,42	1,92	1,68	1,33	0,934	0,630	0,562	0,305	0,247	0,160
СS=2СV
КР%	3,27	2,51	1,94	1,67	1,28	0,918	0,634	0,574	0,342	0,288	0,206
СS=2,5СV
КР%	3,51	2,59	1,95	1,66	1,33	0,906	0,640	0,585	0,373	0,325	0,248

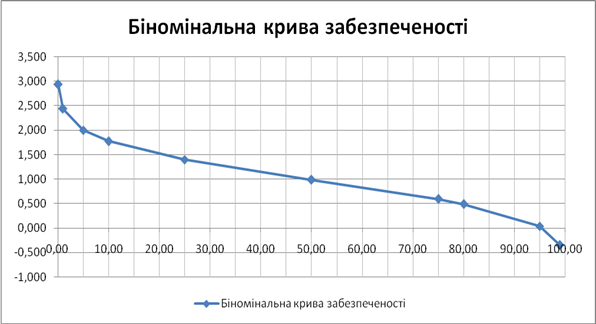
Побудувати біноміальну криву розподілу забезпеченості річного стоку.

Дано: коефіцієнт варіації С_V=0,52 коефіцієнт асиметрії С_S=2С_V=1,2.

Розв'язок: координати біноміальної кривої розподілу знаходимо за виразом К_Р%=Ф_Р%*С_V+1. Розрахунок проводимо у такому порядку: за таблицею додатку 3 знаходимо нормоване відхилення ординати кривої забезпеченості Ф_Р% від середнього значення залежно від С_S і обчислюємо значення К_Р%. результати розрахунків зводимо у тиблицю.

Таблиця

Координати біноміальної кривої забезпеченості річного стоку р. Тетерів

Завдання 4. Розрахунок витрат води заданої забезпеченості

Визначити витрати води забезпеченістю 1, 50 та 80%.

Дано: норма річного стоку р. Тетерів Q₀=2,16 м³/с, крива забезпеченості три параметричного гама-розподілу при С_S=2 С_V

Розв'язок: для визначення розрахункових річних витрат води забезпеченістю 1, 50 та 80% з кривої забезпеченості знімаємо значення К_Р%:

Q_1%=2,16*2,51=5,42 м³/с

Q_50%=2,16*0,92=1,99 м³/с

Q_80%=2,16*0,57=1,23 м³/с

Визначити забезпеченість витрат води 1975 року.

Дано: середньорічна витрата води р. Тетерів у 1975 році Q₁₉₇₅=1,65 м³/с, норма річного стоку Q₀=2,16 м³/с.

Розв'язок: розраховуємо модульний коефіцієнт К_Р за залежністю:

К_Р=Q_P/Q₀=1,65/2,16=0,76, якому за кривою забезпеченості відповідає Р=54%. повторюваність 1 раз на N років розраховуємо за формулою:

N=100/54=2

Тобто, в середньому 1 раз на 2 роки середньорічна витрата води р. Тетерів має бути не меншою, ніж 1,65 м³/с.