Оцениваем качество измерений, вычислив для этого невязки по ходам: по первому - вместе со вторым и по второму - вместе с третьим

2.1.2.10. Оцениваем качество измерений, вычислив для этого невязки по ходам: по первому - вместе со вторым и по второму - вместе с третьим.

Для этого составляем разности координат по соответствующим парам ходов:

Fx=xi-xj

Fy=yi-yj (34)

Одна пара ходов берется с наименьшими периметрами. Подсчеты невязок выписываем внизу таблицы 14.

Относительные невязки не должны превышать 1:1000.

2.1.2.11. Вычисляем веса значений координат узловой точки по формуле:

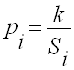
в которой

Si - длина соответствующего хода, выражаем в километрах;

k — произвольный коэффициент, выбираем с таким же расчетом, как и при вычислении дирекционных углов. Результаты вычислений записываем в графу 8 таблица 14.

2.1.2.12. По формуле общей арифметической средины:

где x0 , y0 - приближенные значения координат Х и У,

εxi ,εyi - величины определенные по формулам:

εxi=xi-x0

εyi=yi- y0 (37)

Вычисляем окончательные значения координат узловой точки Х и У. Полученные значение записываем в таблицу 12.

2.1.2.13. Вычисляем невязки приращений координат для каждого хода по формулам:

fx=xi-x0

fy=yi-y0 (33)

и записываем их в графы 5 и 10 таблицу 14.

Выполняем контроль вычисления Х и У и невязок по формулам:

[pfx]=-ωx[p] (39) , [pfy]=-ωy[p] (40)

где ωx и ωy - ошибка округлений при делении [pεx] и [pεy] на [p].

2.1.2.14. Вычисляем для каждого хода в ведомости координат (таблица 12) вторично невязки по формулам:

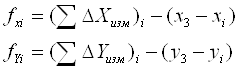
где  и  - измеренные суммы приращений координат по каждому ходу;

Xi и Yi - координаты начальной точки соответствующего хода;

X3 и Y3 - координаты узловой точки (точка 3).

Эти невязки сличают с полученными ранее.

Данные подсчитываем по каждому ходу fабс и fотн. Если последнее не превышают 1:1000, то невязки в приращениях координат распределяем на соответствующие приращения с противоположными знаками, пропорционально длине линий.

Затем в графах 8 и 9 таблица 12 вычисляем исправленные приращения координат.

2.1.2.15. По исправленным приращениям координат вычисляем координаты всех точек (графы 10 и 11 таблица 12).

2.2 Уравновешивание углов сети теодолитных ходов по способу полигонов профессора В.В.Попова

2.2.1 Задание

Уравновесить углы и вычислить дирекционные углы сторон сети, изображенной на рисунке 6.

Исходные данные.

№№ варианта	Дирекционные углы
	αАВ	αСD
24	353°08,2'	35°20,1'

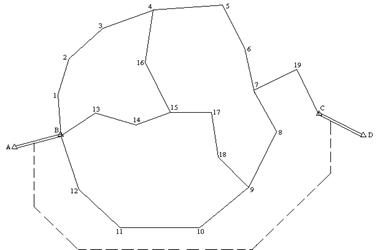
Рис.6 Схема полигонов

2.2.2 Порядок решения

2.2.2.1. Подсчитываем число полигонов, включая и несомкнутый полигон между твердыми (исходными) сторонами АВ и CD.

2.2.2.2. Исправить непосредственно на схеме полигонов (рисунок 6) сумму углов при каждой внутренней узловой точке (15 и 9) для соблюдения условий горизонта (360°), внеся поправки поровну на каждый угол до десяти долей минуты. Поправки записываем на схеме у соответствующих углов в десятых долях минуты. Например, поправку +0,1' записываем в виде +1.

2.2.2.3. Подсчитываем сумму измеренных углов в каждом полигоне с учетом поправок за условие горизонта и записываем ее на схеме внутри соответствующего полигона (см. рисунок 6). Несомкнутый полигон IV, включающий твердые линии АВ и CD условно считаем сомкнутыми при помощи пунктирной линии. Число углов, сторон или направлений по этой пунктирной линии в процессе вычислений считается равным нулю.

Под практической суммой углов в каждом полигоне записываем сумму углов теоретическую, причем по полигону IV теоретическую сумму углов следует вычислять по формуле:

Вычисляем для каждого полигона полученную невязку в сумме углов

и сравниваем ее с предельной,

где n- число углов полигона.

Полученные предельные невязки записываем на схеме (см. рис. 6) под соответствующими суммами углов в каждом полигоне.

2.2.2.4. Составляем схему сети теодолитных ходов для уравновешивания углов (рисунок 7). На этой схеме выписываем номера узловых точек и полигонов. Внутри каждого полигона под его номером заготовить табличку невязок и около каждого звена, кроме пунктирного, таблички поправок. В таблички записываем полученные невязки.

2.2.2.5. Вычисляем красные числа для каждого звена всех полигонов по правилу: красное число звена равно числу направлений в звене, деленному на число направлений в полигоне.

При этом каждую линию в замкнутых полигонах |,||, и ||| а в полигоне IV твердые линии АВ и СD считаем каждую за одно направление. Поэтому на чертеже пунктирная линия, условно замыкающая полигон, вычерчивается у середины твердых линий, включая в полигоне не целые линии, а одно направление.

Контроль: сумма красных чисел по каждого полигону должна быть точно равна единице. Красные числа выписать красным цветом под соответствующими табличками.

2.2.2.6.Распределяем невязки пропорционально красным числам соответствующих полигонов. Начинаем с полигона, имеющего наибольшую по абсолютной величине невязку, умножая, ее последовательно на красные числа звеньев данного полигона и вносим произведения в соответствующие таблички поправок со знаком невязки, с округлением до 0.1΄