Подсчитываем алгебраические суммы чисел, а таблицу поправок и записываем их над двойной чертой

2.2.2.7. Подсчитываем алгебраические суммы чисел, а таблицу поправок и записываем их над двойной чертой.

Подсчитываем поправки во внутренние углы каждого полигона по всем звеньям. Для внутренних звеньев сети поправки получаем так: изменяем знак суммы чисел внешней по отношению к полигону таблички и складываем с суммой чисел внутренней таблички того же знака. Для каждого внешнего звена сети поправка равна итогу внешней таблички с противоположным знаком. Все поправки на звенья записываем в скобках внутри полигона у соответствующих звеньев (см. рис. 7).

Контроль вычислений поправок: их сумма по каждому полигону должна быть равна невязке полигона с обратным знаком.

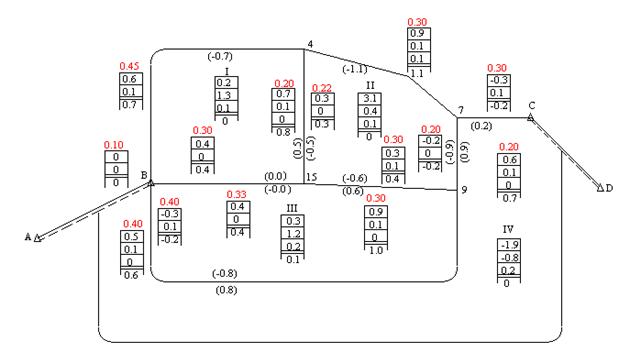
Рис.7 Схема уравновешивания

1757°49,8' 1032°35,1'

 1757°48,1'  1032°33,1'

+1,7' +2,0'

 3,3'  2,6'

1030°24,5' 407°25,6'

 1030°25,1'  407°26,0'

-0,6' -0,4'

 2,6'  1,7'

2.2.2.8. Распределение поправки звеньев на каждый угол.

Для этого поправку, приходящуюся на звено, делим на число направлений и полученную поправку направления вводим в углы при узловых точках, а в остальные углы – удвоенную поправку. Следовательно, каждый угол при узловой точке должен получить по две поправки, приходящиеся на этот угол от каждого направления обоих звеньев.

Поправки углов записываем под (или над) соответствующими углами непосредственно на схеме (рис.6). При узловых точках поправки от каждого звена записываем отдельно.

2.2.2.9. Выписываем в ведомость вычисления дирекционных углов со схематического чертежа измеренные углы и на нем соответствующие поправки. Подсчитываем допустимую невязку и сравниваем с ней полученную. Контроль: сумма поправок должна быть равна полученной невязке с противоположным знаком. Выписываем исправленные углы, подсчитываем для контроля их суммы и вычисляем дирекционные углы сторон всех ходов.

2.3 Уравновешивание системы полигонометрических ходов способом последовательных приближений

2.3.1 Задание

По данным, указанным на схеме полигонометрических ходов (рис. 8, 9), способом последовательных приближений произвести уравновешивание:

• дирекционных углов узловой линий;

• координат узловых точек.

В таблице 17 приведены по вариантам углы при точках № 1,12,16. Остальные углы принять такими же, как и на схеме (см. рис. 8).

Таблица 17

Значения углов № 1,12,16.

№№ варианта		Углы
		1	12	16
24	140°00’48’’		125°34’36’’	150°06’51’’

Таблица 18

Суммы приращений координат по звеньям.

№№ варианта	Суммы приращений координат
	Звено 1	Звено 2	Звено 3	Звено 4	Звено 5	Звено 6
24	+670,50 +954,10	+472,45 +2972,97	+595,90 +872,40	-1475,65 +253,55	-2568,70 -4242,67	+1002,95 -3225,53

2.3.2.2 Порядок уравновешивания.

2.3.2.1.Вычисление дирекционных углов.

2.3.2.1.1. На схематическом чертеже (см. рис. 8) у каждого звена выписываем в виде дроби: в числителе номер звена и сумму измеренных углов, в знаменателе - число углов (звеном называют часть хода, заключенного между угловыми линиями или между «твердой» и узловой линией).

2.3.2.1.2. По данным, представленным на чертеже, подсчитываем угловые невязки по ходам и замкнутому полигону и выписываем их на чертеж (см. рис. 8). Если угловые невязки не превышают допустимой, то продолжаем вычисление.

2.3.2.1.2. Заполняем ведомость вычисления дирекционных углов (таблица 19) в следующем порядке:

• выписываем исходные данные дирекционные углы «твердых» линий с чертежа сети;

• в графу 1 выписываем название узловых линий, для которых вычисляются дирекционные углы;

• в графу 2 выписываем наименование начальных (исходных) линий (твердых и узловых) звена, от которых можно вычислить искомые дирекционные углы, при этом в первую очередь выписываем наименование «твердых», исходных сторон;

• в графу 3 выписываем номера звеньев примыкающих к соответствующей узловой (искомой) линии, графы 4, 5 и 6 заполняем со схемы ходов в соответствии с их названием;

• вычисляем веса дирекционных углов по каждому звену (до 0,01) по формуле:

где i = 1,2,3,... „- номер звена; k - произвольный постоянный коэффициент обычно выбираем так, чтобы веса выражались числами близкими к единице;

ni - число углов звена.

Для дирекционного угла каждой узловой линии вычисляем сумму весов примыкающих к ней звеньев и определяем веса по формуле:

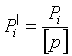
Контроль:[P΄]=1

• вычисляем методом последовательных приближений значения дирекционных углов узловых линий.

Нулевое приближение для дирекционных углов каждой узловой линии вычисляем непосредственно от « твердой» стороны:

 (48)

 (49)

Нулевое приближение записываем в первых строках каждого блока графы 9 и подчеркиваем;

• для вычисления первого приближения дирекционного угла каждой узловой линии находим значения дирекционного угла этой линии путем передачи от исходных данных по воем примыкающим к ней звеньям. Из полученных значений найти среднее весовое значение (графы 9,10)

где α0 - приближенное (наименьшее) значение дирекционного угла узловой линии (взятое до целых минут) из полученных значений по каждому примыкающему звену:

Это и будет первым приближением.

Аналогично вычисляем второе, а затем и следующие приближения (графы 11,...). При вычислении каждого последующего приближения за исходные данные принимаем самые последние значения приближений.

Приближения заканчиваем тогда, когда последнее вычисленное приближение дает одинаковый результат с предыдущим. Это последнее приближение и является окончательным значением о. Величины εi и α вычисляем до целых секунд;

• для контроля вычислений определяем поправки в углы по звеньям.

 (углы левые), (52)

где α и αi - значения дирекционных углов соответственно узловой линии, записанные в графы последнего приближения, и окончательное.

Выполнение равенства: (53)

служит контролем правильности вычисления окончательного значения дирекционного угла.

Из-за погрешностей округления Σ P`iνi может быть не равно нулю, но должна быть

Значения поправок νi выписать на схему ходов (см. рис. 8) красным цветом над суммой измеренных углов соответствующего звена и произвести подсчет поправок по ходам, имея в виду, что т.е. в случае правых углов знак полученной поправки должен быть изменен на противоположный.

Контроль: сумма поправок по ходу должна быть равна невязке с обратным знаком.

Таблица 19

Вычисление дирекционных углов узловых точек.

№ линии		№ звена	Суммауглов взвене	Число углов	Углы β и λ	Веса		Приближенияиближалн
Искомой	Исходной					P	P`		P`ε	||	P`ε	|||	P`ε	IV	P`ε	V	P`ε	VI	P`ε	VII	P`ε	νλ	P`νλ
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
2-15	АВ 11-14 16-7	1 6 2	500°07'30'' 280°12'52'' 854°49'04''	3 2 6	П П Л	2 3 1	0,33 0,50 0,17	190°02'54'' 1'18'' 1'46''	0 12 9	54 0 25	0 3 5	54 6 36	0 6 7	54 2 34	0 4 7	54 4 35	0 5 7	54 3 35	0 5 7			12 3 -29	3,96 1,5 -4,93
						6,0	1,00	1'15''	21	2	8	7	13	5	11	6	12	6	12				0,53
11-14	EF 2-15 16-7	5 6 4	328°51'38'' 280°12'52'' 664°58'32''	3 2 5	Л Л П	2 3 1,2	0,32 0,48 0,20	290°15'50'' 46'' 1'10''	1 0 5	50 7 49	0 9 0	50 54 00	0 2 2	50 59 58	0 4 2	50 57 59	0 3 2	50 58 59	0 4 2	50 58 59	0 4 2	6 -2 -3	1,92 -0,96 -0,6
						6,2	1,00	52''	6	58	9	54	4	56	6	55	5	56	6	56	6		0,36
16-7	DС 15-2 14-11	3 2 4	475°06'18'' 854°49'04'' 664°58'32''	2 6 5	Л П Л	3 1 1,2	0,58 0,19 0,23	55°14'42'' 13'50'' 13'54''	30 0 1	42 11 24	18 0 3	42 58 26	26 0 6	42 3 26	23 0 5	42 1 28	24 0 6					-11 30 3	-6,38 5,7 0,69
						5,2	1,00	14''21''	31	21	21	30	32	31	28	31	30						0,01

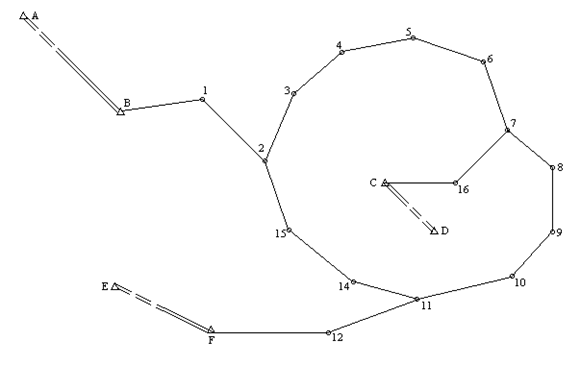
Рис.8 Схема для вычисления дирекционных углов опорных линий

2.3.2.2. Вычисление координат.

2.3.2.2.1. По данным, указанным на чертеже (рис. 9), подсчитываем линейные невязки по ходам и по замкнутому полигону и выписываем их на чертеже.

Если fотн ≤1/5000 (56), то производим дальнейшие вычисления.

2.3.2.2.2. По имеющимся на чертеже данным заполнить ведомость вычисления координат (табл.20).

а) выписываем исходные координаты «твердых» пунктов;

б) выписываем названия искомых узловых и исходных точек в том же порядке, как и при вычислении дирекционных углов;

в) выписываем номера звеньев, примыкающих к исходной узловой точке;

г) выписываем суммы приращений ∑Δхпр и ∑Δупр и периметры ∑di для каждого звена;

д) вычисляем веса сумм приращений координат по каждому звену по формулам:

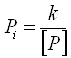
Контроль:е) вычисляем нулевые приближения координат узловых точек путем передачи координат по одному звену от твердых точек:

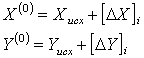
и записываем в первых строках каждого блока графы 8 таблицы 20.

ж) аналогично вычисляем, дирекционных углов получаем первые, вторые и т.д. приближения координат узловых точек по формулам:

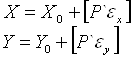
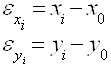
где X0 и Y0 - приближенные значения координат узловой точки, взятые до целого центра;

X , Y- значения координат узловой точки полученные по каждому звену. Значения pi , εx и εy, вычислить в сантиметрах с округлением до 1 см;

з) для контроля вычислений определяем поправки νx1 и νy1 в суммах приращений по ходам. Эти поправки равны разностям между окончательными значениями координат и значениями, записанными в той же графе, которые получены по отдельным звеньям.

Контролем правильности вычислении среднего весового приращения координат для каждой узловой точки служит равенство: (62)

Вследствие погрешностей округлений равенство (62) точно не выполняется, но должно быть (63)

Поправки в приращениях записываем в графу 14 таблицы 20, а так же выписываем красным цветом на схеме (см. рисунок 9) над соответствующими суммами приращений. Следует иметь ввиду, что знак поправок соответствует приращению хода, указанному стрелкой.

Контроль: сумма поправок по отдельным ходам равна невязке с обратным знаком.

Вычисление ординат узловых точек

Ув=25763,05м Ус=28817,35м УF=25700,48м

Таблица 20

Вычисление абцисс узловых точек

Хв=31361,65м Хс=31908,90м ХF=28461,05м

пункты		№ звена	Суммаприращенийвзвене	Длина звена, км	Веса		Приближенияиближалн
Искомый	Исходный				P	P`		P`ε	||	P`ε	|||	P`ε	IV	P`ε	V	P`ε	VI	P`ε	νλ	P`νλ
1	2	3	4	56	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
2	В 7 11	1 2 6	670,50 -472,45 1002,95	1,1 4,0 5,3	3,64 1,00 0,75	0,68 0,18 0,14	32032, 15 35 90	0 4 11	15 45 1,34	0 5 17	15 36 49	0 4 5	15 42 48	0 5 5	15 39 46	0 4 4	15 39 45	0 4 4	8 -16 -22	5,44 -2,88 -3,08
					5,39	1,00	30	15	37	22	24	9	25	10	23	8	23	8		-0,52
7	С 2 11	3 2 4	595,90 472,45 1475,65	1,3 4,0 4,8	3,08 1,00 0,83	0,63 0,20 0,17	32504, 80 60 1,60	13 0 17	80 75 95	3 0 3	80 82 1,19	0 0 7	80 69 1,18	7 0 8	80 70 1,16	6 0 8	95 28 19		4 14 -32	2,52 2,8 -5,44
					4,91	1,00	90	30	81	6	87	7	84	15	84	14	50			-0,12
11	F 2 7	5 6 4	2568,90 -1002,95 -1475,65	4,4 5,3 4,8	0,91 0,75 0,83	0,37 0,30 0,33	31029, 95 28,95 15	37 0 7	95 35 25	26 3 0	95 42 16	29 8 0	95 29 22	27 2 0	95 30 19	28 3 0	95 28 19	28 3 0	-45 22 31	-16,65 6,6 10,23
					2,49	1,00	39	44	54	29	53	37	51	29	50	31	50	31		0,18
2	В 7 11	1 2 6	954,10 -2972,97 -3225,53	1,1 4,0 5,3	3,64 1,00 0,75	0,68 0,18 0,14	26716, 1,15 78 1,57	25 0 11	11,5 82 1,51	22 0 10							-1 32 -37		-0,68 5,76 -5,18
					5,39	1,00	1,14	36	1,14	32									-0,1
7	С 2 11	3 2 4	872,40 2972,97 -253,55	1,3 4,0 4,8	3,08 1,00 0,83	0,63 0,20 0,17	29689, 75 1,12 55	13 11 0	75 1,11 49	16 12 0	75 1,11 50	16 12 0	75 1,11 49	16 12 0	75 1,11 50	16 12 0	2 -34 28		1,26 -6,8 4,76
					4,91	1,00	79	24	77	28	78	28	77	28	78	28			-0,78
11	F 2 7	5 6 4	4242,62 3225,53 253,55	4,4 5,3 4,8	0,91 0,75 0,83	0,37 0,30 0,33	29942, 1,10 0,67 1,30	16 0 21	1,10 67 1,34	16 0 22	1,10 67 1,32	16 0 21	1,10 67 1,33	16 0 22	1,10 67 1,32	16 0 21	-5 38 -28		-1,85 11,4 -9,24
					2,49	1,00	1,04	37	1,05	38	1,04	37	1,05	38	1,04	37			0,31