Навигация
Решить задачу линейного программирования, используя
1.2 Решить задачу линейного программирования, используя
табличный симплексный метод
Предприятию необходимо выпустить 2 вида изделий (Р1; Р2). Есть 3 вида станков (Т1; Т2; Т3), каждый из которых может обрабатывать изделия всех видов.
Продолжительность обработки
на станке 1-го типа изделий 1-го типа 4 единицы
на станке 2-го типа изделий 1-го типа 1 единица
на станке 3-го типа изделий 1-го типа 1 единица
на станке 1-го типа изделий 2-го типа 0 единиц
на станке 2-го типа изделий 2-го типа 2 единицы
на станке 3-го типа изделий 2-го типа 4 единицы
Доход от реализации изделия первого типа составляет 6 единиц, второго типа – 6 единиц.
Запас мощности (рабочее время станка) 1-о типа – 20 единиц, 2-го типа 37 единиц, 3-го типа – 40 единиц.
Составить такой план загрузки станков, при котором себестоимость выпуска продукции будет минимальной.
Решение
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Симплекс метод принадлежит к числу аналитических методов решения основной задачи линейного программирования.
Составим линейные уравнения для решения задачи.
F (x) = 6х1 + 6 х2 →max – целевая функция.
где х1 – количество изделий Р1;
х2 - количество изделий Р2.
Уравнения ограничений :
4 х1 ≤ 20;
х1 + 2 х2 ≤ 37;
х1 + 4 х2 ≤ 40.
Найдем наибольшее значение линейной функции
F = 6 x1 + 6 x2
при следующих ограничениях

Нам необходимо найти начальное опорное ( абсолютно произвольное ) решение для исходной функции, которое бы удовлетворяло системе наложенных ограничений. Далее, применяя симплекс таблицы, мы будем получать решения, при которых значение функции будет, как минимум, не убывать. И так до тех пор, пока не достигнем оптимально решения, при котором функция достигает своего максимума. Если, конечно, рассматриваемая нами линейная функция обладаем максимальным значением при заданной системе ограничений. Перед применением симплекс таблиц, необходимо преобразовать систему линейных ограничений и рассматриваемую нами функцию к вполне определенному виду.
Свободные члены системы ограничений положительны. Выполнено одно из необходимых условий применения симплекс метода.
К левой части неравенства 1 системы ограничений прибавляем неотрицательную переменную x3 , тем самым мы преобразуем неравенство 1 в равенство.
К левой части неравенства 2 системы ограничений прибавляем неотрицательную переменную x4 , тем самым мы преобразуем неравенство 2 в равенство.
К левой части неравенства 3 системы ограничений прибавляем неотрицательную переменную x5 , тем самым мы преобразуем неравенство 3 в равенство.
Введенные нами переменные имеют вполне конкретный физический смысл, непосредственно связанный с условием нашей задачи.
4 x1 + x3 = 20
x1 + 2 x2 + x4 = 37
x1 + 4 x2 + x5 = 40
Система ограничений приведена к каноническому виду, т.е все условия системы представляют собой уравнения. Выполнено еще одно из необходимых условий применения симплекс метода.
Определимся с начальным опорным решением. Наличие единичного базиса в системе ограничений позволяет легко найти начальное опорное решение. Рассмотрим подробнее.
Переменная x3 входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x3 - базисная переменная.
Переменная x4 входит в уравнение 2 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x4 - базисная переменная.
Переменная x5 входит в уравнение 3 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x5 - базисная переменная.
Переменные , которые не являются базисными называются свободными переменными. Приравняв свободные переменные нулю в получившийся системе ограничений мы получим начальное опорное решение.
X нач = ( 0 , 0 , 20 , 37 , 40 )
Вернемся к рассмотрению функции F.
F = 6 x1 + 6 x2
Линейная функция F не содержат базисных переменных.
Для составления начальной симплекс таблицы мы выполнили все условия.
В процессе дальнейших преобразований возможны два случая. Если в симплекс таблице, на каком то шаге, мы получим строку F состоящую из положительных элементов, это будет означать, что мы нашли оптимальное решение. В противном случае функция не ограничена.
При составлении исходной симплекс таблицы, коэффициенты при переменных функции F записываются с противоположными знаками, а свободный член со своим знаком.
За ведущий выберем столбец 1 , так как -6 наименьший элемент в F строке. Элемент F строки, принадлежащий столбцу свободных членов не рассматриваем.
За ведущую выберем строку 1, так как отношение свободного члена к соответствующему элементу выбранного столбца для 1 строки является наименьшим. Обратите внимание, что отношение мы вычисляем только для положительных элементов столбца 1.
| базисные переменные | x1 | x2 | x3 | x4 | x5 | свободные члены | отношение |
| x3 | 4 | 0 | 1 | 0 | 0 | 20 | 5 |
| x4 | 1 | 2 | 0 | 1 | 0 | 37 | 37 |
| x5 | 1 | 4 | 0 | 0 | 1 | 40 | 40 |
| F | -6 | -6 | 0 | 0 | 0 | 0 | - |
Разделим элементы строки 1 на 4.
| базисные переменные | x1 | x2 | x3 | x4 | x5 | свободные члены | отношение |
| x3 | 1 | 0 | 1/4 | 0 | 0 | 5 | 5 |
| x4 | 1 | 2 | 0 | 1 | 0 | 37 | 37 |
| x5 | 1 | 4 | 0 | 0 | 1 | 40 | 40 |
| F | -6 | -6 | 0 | 0 | 0 | 0 | - |
От элементов строки 2 отнимает соответствующие элементы строки 1 .
От элементов строки 3 отнимает соответствующие элементы строки 1 .
От элементов строки F отнимает соответствующие элементы строки 1, умноженные на -6.
За ведущий выберем столбец 2 , так как -6 наименьший элемент в F строке. Элемент F строки, принадлежащий столбцу свободных членов не рассматриваем.
За ведущую выберем строку 3, так как отношение свободного члена к соответствующему элементу выбранного столбца для 3 строки является наименьшим. Обратим внимание, что отношение мы вычисляем только для положительных элементов столбца 2.
| базисные переменные | x1 | x2 | x3 | x4 | x5 | свободные члены | отношение |
| x1 | 1 | 0 | 1/4 | 0 | 0 | 5 | - |
| x4 | 0 | 2 | -1/4 | 1 | 0 | 32 | 16 |
| x5 | 0 | 4 | -1/4 | 0 | 1 | 35 | 35/4 |
| F | 0 | -6 | 3/2 | 0 | 0 | 30 | - |
Разделим элементы строки 3 на 4.
| базисные переменные | x1 | x2 | x3 | x4 | x5 | свободные члены | отношение |
| x1 | 1 | 0 | 1/4 | 0 | 0 | 5 | - |
| x4 | 0 | 2 | -1/4 | 1 | 0 | 32 | 16 |
| x5 | 0 | 1 | -1/16 | 0 | 1/4 | 35/4 | 35/4 |
| F | 0 | -6 | 3/2 | 0 | 0 | 30 | - |
От элементов строки 2 отнимает соответствующие элементы строки 3, умноженные на 2.
От элементов строки F отнимает соответствующие элементы строки 3, умноженные на -6.
| базисные переменные | x1 | x2 | x3 | x4 | x5 | свободные члены | отношение |
| x1 | 1 | 0 | 1/4 | 0 | 0 | 5 | - |
| x4 | 0 | 0 | -1/8 | 1 | -1/2 | 29/2 | - |
| x2 | 0 | 1 | -1/16 | 0 | 1/4 | 35/4 | - |
| F | 0 | 0 | 9/8 | 0 | 3/2 | 165/2 | - |
На основании F строки полученной симплекс таблицы, выпишем выражение функции
F = 165/2 -9/8 x3 -3/2 x5
Учитывая, что все x i ≥0 по условию задачи, наибольшее значение функции равно свободному члену 165/2.
Другими словами, учитывая правило формирования симплекс таблицы, критерием получения оптимального решения является отсутствия отрицательных элементов в строке F ( свободный член может быть отрицательным). Что мы непосредственно и получили.
Теперь можем записать ответ.
Ответ :
X опт = ( 5 , 35/4 , 0 , 29/2 , 0 )
Значение функции : F = 165/2
Задание 2. Имитационное моделирование. Сети Петри
Похожие работы
... в разработке методов превращения разнообразной конструкторской документации в цифровую форму и представлении всех задач и элементов процесса проектирования только в виде операций над числами и логическими выражениями с доведением их до алгоритмов и машинных программ. Но при автоматизации проектно-конструкторского процесса следует постоянно помнить, что ЭВМ — это вспомогательное средство, а не ...
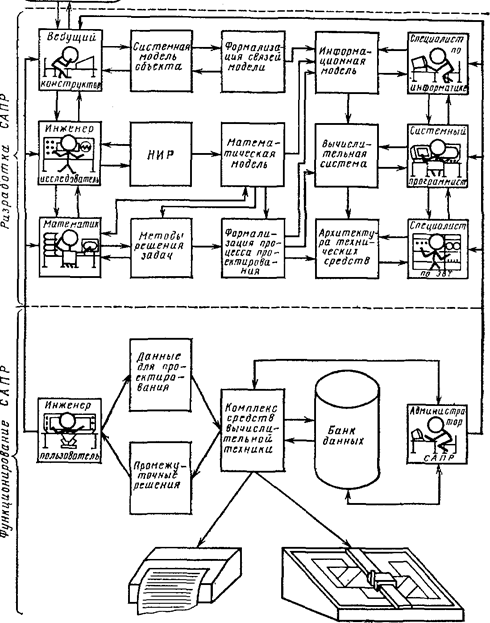
... вующих систем автоматизированного проектирования подтвердил отсутствие разработок по автоматизации схемотехнического и функци- онального проектирования объектов класса ВКА. . - 41 - 2. СИСТЕМНЫЙ АНАЛИЗ ВАКУУМНОЙ КОММУТАЦИОННОЙ АППАРАТУРЫ 2.1. Системная модель ВКА при функциональном и схемотехни- ческом проектировании. Анализ существующих конструкций ВКА ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... функциональных возможностей; - улучшение эргономических качеств; - улучшение эстетических качеств; - повышение чувствительности, точности, стабильности, диапазона. Цели и задачи автоматизации производственных систем Автоматизация - это совокупность организационно-технических мероприятий, обеспечивающих замену физического и умственного труда человека, затрачиваемого на планирование, ...






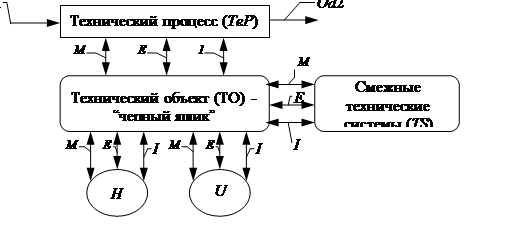


0 комментариев