Навигация
Теоретичні положення з організації моделювання транспортних мереж
3 Теоретичні положення з організації моделювання транспортних мереж
Задачу пошуку найкоротшого шляху між джерелом і стоком (початковий і кінцевий пункти мережі) можна вирішити за допомогою алгоритму Дейкстри. Алгоритм Дейкстри розроблений для знаходження найкоротшого шляху між заданим вихідним вузлом і будь-яким іншим вузлом мережі.
У процесі виконання цього алгоритму при переході від вузла ![]() до наступного вузла
до наступного вузла ![]() використовується спеціальна процедура позначки ребер. Позначимо через
використовується спеціальна процедура позначки ребер. Позначимо через ![]() найкоротшу відстань від вихідного вузла 1 до вузла
найкоротшу відстань від вихідного вузла 1 до вузла ![]() , через
, через ![]() – довжину ребра
– довжину ребра ![]() . Тоді для вузла
. Тоді для вузла ![]() визначимо мітку
визначимо мітку ![]() в такий спосіб:
в такий спосіб:
![]()
Мітки вузлів в алгоритмі Дейкстри можуть бути двох типів: тимчасові і постійні. Тимчасова мітка згодом може бути замінена на іншу тимчасову, якщо буде знайдений більш короткий шлях до даного вузла. Коли ж стане очевидним, що не існує більш короткого шляху від вихідного вузла до даного, статус тимчасової мітки змінюється на постійний.
Розрахункова схема алгоритму складається з наступних кроків.
Крок 0. Вихідному вузлу (вузол 1) привласнюється мітка ![]() . Думаємо
. Думаємо ![]() .
.
Крок i. а) Обчислюються тимчасові мітки ![]() для усіх вузлів
для усіх вузлів ![]() , які можна досягти безпосередньо з вузла
, які можна досягти безпосередньо з вузла ![]() , і які не мають постійних міток. Якщо вузол
, і які не мають постійних міток. Якщо вузол ![]() уже має мітку
уже має мітку ![]() , отриману від іншого вузла
, отриману від іншого вузла ![]() , і якщо
, і якщо ![]() , тоді мітка
, тоді мітка ![]() заміняється на
заміняється на ![]() .
.
б) Якщо усі вузли мають постійні мітки, процес обчислень закінчується. У противному випадку вибирається мітка ![]() з найменшим значенням відстані
з найменшим значенням відстані ![]() серед усіх тимчасових міток (якщо таких міток декілька, то вибір довільний). Думаємо
серед усіх тимчасових міток (якщо таких міток декілька, то вибір довільний). Думаємо ![]() і повторюємо крок
і повторюємо крок ![]() .
.
Задача визначення найкоротших відстаней між елементами транспортної мережі (Алгоритм Флойда).
Дана задача вирішується за допомогою алгоритму Флойда.
Цей алгоритм більш загальний у порівнянні з алгоритмом Дейкстри, тому що він знаходить найкоротші шляхи між будь-якими двома вузлами мережі. У цьому алгоритмі мережа представлена у виді квадратної матриці з ![]() рядками і
рядками і ![]() стовпцями. Елемент
стовпцями. Елемент ![]() дорівнює відстані
дорівнює відстані ![]() від вузла
від вузла ![]() до вузла
до вузла ![]() , що має кінцеве значення, якщо існує дуга
, що має кінцеве значення, якщо існує дуга ![]() , і дорівнює нескінченності в противному випадку.
, і дорівнює нескінченності в противному випадку.
Покажемо спочатку основну ідею методу Флойда. Нехай є три вузли ![]() і задані відстані між ними (рис. 3.1). Якщо виконується нерівність
і задані відстані між ними (рис. 3.1). Якщо виконується нерівність ![]() , то доцільно замінити шлях
, то доцільно замінити шлях ![]() шляхом
шляхом ![]() . Така заміна (далі її будемо умовно називати трикутним оператором) виконується систематично в процесі виконання алгоритму Флойда.
. Така заміна (далі її будемо умовно називати трикутним оператором) виконується систематично в процесі виконання алгоритму Флойда.
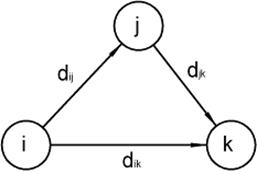
Рис. 3.1. Трикутний оператор
Алгоритм Флойда вимагає виконання наступних дій.
Крок 0. Визначаємо початкову матрицю відстаней ![]() і матрицю послідовності вузлів
і матрицю послідовності вузлів ![]() . Діагональні елементи обох матриць позначаються знаком «–», що показує, що ці елементи в обчисленнях не беруть участь. Думаємо
. Діагональні елементи обох матриць позначаються знаком «–», що показує, що ці елементи в обчисленнях не беруть участь. Думаємо ![]() :
:

Рис. 3.2. Початкова ситуація
Основний крок k. Задаємо рядок ![]() і стовпець
і стовпець ![]() як ведучий рядок і ведучий стовпець. Розглядаємо можливість застосування трикутного оператора до всіх елементів
як ведучий рядок і ведучий стовпець. Розглядаємо можливість застосування трикутного оператора до всіх елементів ![]() матриці
матриці ![]() . Якщо виконується нерівність
. Якщо виконується нерівність ![]() , тоді виконуємо наступні дії:
, тоді виконуємо наступні дії:
· створюємо матрицю ![]() шляхом заміни в матриці
шляхом заміни в матриці ![]() елемента
елемента ![]() на суму
на суму ![]() ,
,
· створюємо матрицю ![]() шляхом заміни в матриці
шляхом заміни в матриці ![]() елемента
елемента ![]() на
на ![]() . Думаємо
. Думаємо ![]() і повторюємо крок
і повторюємо крок ![]() .
.
Пояснимо дії, виконувані на ![]() -м кроці алгоритму, представивши матрицю
-м кроці алгоритму, представивши матрицю ![]() так, як вона показана на рис 3.3. На цьому рисунку рядок
так, як вона показана на рис 3.3. На цьому рисунку рядок ![]() і стовпець
і стовпець ![]() є ведучими. Рядок
є ведучими. Рядок ![]() – будь-який рядок з номером від 1 до
– будь-який рядок з номером від 1 до ![]() , а рядок
, а рядок ![]() – довільний рядок з номером від
– довільний рядок з номером від ![]() до
до ![]() . Аналогічно стовпець
. Аналогічно стовпець ![]() представляє будь-як стовпець з номером від 1 до
представляє будь-як стовпець з номером від 1 до ![]() , стовпець
, стовпець ![]() – довільний стовпець з номером від
– довільний стовпець з номером від ![]() до
до ![]() . Трикутний оператор виконується в такий спосіб. Якщо сума елементів ведучих рядка і стовпця (показаних у квадратах) менше елементів, що знаходяться в перетинанні стовпця і рядка (показаних у кружках), що відповідають розглянутим ведучим елементам, то відстань (елемент у кружку) заміняється на суму відстаней, представлених ведучими елементами:
. Трикутний оператор виконується в такий спосіб. Якщо сума елементів ведучих рядка і стовпця (показаних у квадратах) менше елементів, що знаходяться в перетинанні стовпця і рядка (показаних у кружках), що відповідають розглянутим ведучим елементам, то відстань (елемент у кружку) заміняється на суму відстаней, представлених ведучими елементами:
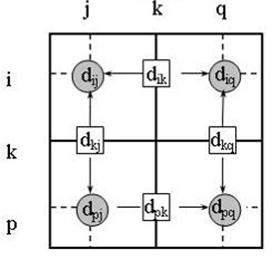
Рис. 3.3. Ілюстрація алгоритму Флойда
Після реалізації ![]() кроків алгоритму визначення по матрицях
кроків алгоритму визначення по матрицях ![]() і
і ![]() найкоротшому шляху між вузлами
найкоротшому шляху між вузлами ![]() і
і ![]() виконується за наступними правилами.
виконується за наступними правилами.
1. Відстань між вузлами ![]() і
і ![]() дорівнює елементові
дорівнює елементові ![]() в матриці
в матриці ![]() .
.
2. Проміжні вузли шляху від вузла ![]() до вузла
до вузла ![]() визначаємо по матриці
визначаємо по матриці ![]() . Нехай
. Нехай ![]() , тоді маємо шлях
, тоді маємо шлях ![]() . Якщо далі
. Якщо далі ![]() і
і ![]() , тоді вважаємо, що весь шлях визначений, тому що знайдені всі проміжні вузли. У противному випадку повторюємо описану процедуру для шляхів від вузла
, тоді вважаємо, що весь шлях визначений, тому що знайдені всі проміжні вузли. У противному випадку повторюємо описану процедуру для шляхів від вузла ![]() до вузла
до вузла ![]() і від вузла
і від вузла ![]() до вузла
до вузла ![]() .
.
При аналізі транспортних мереж часто виникає задача визначення максимального потоку, що може пропустити дана мережа, а також задача розподілу цього потоку по дугах мережі.
З математичної точки зору задача про максимальний потік формулюється в такий спосіб: при заданій конфігурації мережі і відомої пропускної здатності ![]() знайти ненегативні значення
знайти ненегативні значення ![]() , що задовольняють умовам і, що максимізують функцію
, що задовольняють умовам і, що максимізують функцію ![]() , тобто
, тобто
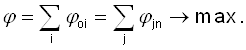
Алгоритм для знаходження максимального потоку був запропонований Фордом і Фалкерсоном і полягає в поступовому збільшенні потоку, що пропускається по мережі, доти, поки він не стане найбільшим. Алгоритм заснований на теоремі Форда-фалкерсона: у будь-якій транспортній мережі максимальний потік із джерела ![]() в стік
в стік ![]() , дорівнює мінімальній пропускній здатності розрізу, що відокремлює
, дорівнює мінімальній пропускній здатності розрізу, що відокремлює ![]() від
від ![]() .
.
Крок 0. Призначаємо вузлові 15 постійну мітку [0, -].
Крок 1. З вузла 15 можна досягти вузлів 21 2 12. Обчислюємо мітки для цих вузлів, у результаті одержуємо наступну таблицю міток:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 21 | [512,15] | Тимчасова |
| 2 | [237,15] | Тимчасова |
Серед вузлів 21, 2, 12, вузол 12 має найменше значення відстані (U12=172). Тому статус мітки цього вузла змінюється на «постійна».
Крок 2. З вузла 12 можна потрапити у вузли 2, 23, 22. Одержуємо наступний список вузлів.
Тимчасовий статус мітки [237,15] вузла 2 заміняється на постійний (U2=237).
Крок 3. З вузла 2 можна досягти вузлів 21, 22, 31. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Тимчасова |
| 21 | [370+512,2]=[882,2] | Тимчасова |
| 22 | [1009,12] | Тимчасова |
| 22 | [696+237,2]=[933,2] | Тимчасова |
| 23 | [810,12] | Тимчасова |
| 31 | [655+237,2]=[892,2] | Тимчасова |
Тимчасовий статус мітки [512,15] вузла 21 заміняється на постійний (U21=512).
Крок 4. З вузла 21 можна досягти вузлів 31. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 22 | [933,2] | Тимчасова |
| 23 | [810,12] | Тимчасова |
| 31 | [892,2] | Тимчасова |
| 31 | [512+289,21]= [801,21] | Тимчасова |
Тимчасовий статус мітки [801,21] вузла 31 заміняється на постійний (U31=801).
Крок 5. З вузла 31 можна досягти вузлів 22, 38. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 31 | [801,21] | Постійна |
| 22 | [933,2] | Тимчасова |
| 22 | [801+237,31]= [1038,31] | Тимчасова |
| 23 | [810,12] | Тимчасова |
| 38 | [801+197,31]= [992,31] | Тимчасова |
Тимчасовий статус мітки [810,12] вузла 23 заміняється на постійний (U23=810).
Крок 6. З вузла 23 можна досягти вузла 22, 38, 3. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 31 | [801,21] | Постійна |
| 23 | [810,12] | Постійна |
| 22 | [933,2] | Тимчасова |
| 22 | [810+535,23]= [1345,23] | Тимчасова |
| 38 | [992,31] | Тимчасова |
| 38 | [810+929,23]= [1739,23] | Тимчасова |
| 3 | [810+1045,23]= [1855,23] | Тимчасова |
Тимчасовий статус мітки [933,2] вузла 22 заміняється на постійний (U22=933).
Крок 7. З вузла 22 можна досягти вузлів 38, 3. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 31 | [801,21] | Постійна |
| 23 | [810,12] | Постійна |
| 22 | [933,2] | Постійна |
| 38 | [992,31] | Тимчасова |
| 38 | [933+427,22]= [1360,22] | Тимчасова |
| 3 | [1855,23] | Тимчасова |
| 3 | [933+938,22]= [1871,22] | Тимчасова |
Тимчасовий статус мітки [992,31] вузла 38 заміняється на постійний (U38=992).
Крок 8. З вузла 38 можна досягти вузла 3. Після обчислення міток одержимо наступний їх список:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 31 | [801,21] | Постійна |
| 23 | [810,12] | Постійна |
| 22 | [933,2] | Постійна |
| 38 | [992,31] | Постійна |
| 3 | [1855,23] | Тимчасова |
| 3 | [992+116,38]= [1108,38] | Тимчасова |
На останньому кроці знайдено найкоротшу відстань для вузла 3 – [1108.38]. Таким чином статус мітки вузла 3 змінюється на постійний.
Кінцевий результат міток має такий вигляд:
| Вузол | Мітка | Статус мітки |
| 15 |
| Постійна |
| 12 | [172,15] | Постійна |
| 2 | [237,15] | Постійна |
| 21 | [512,15] | Постійна |
| 31 | [801,21] | Постійна |
| 23 | [810,12] | Постійна |
| 22 | [933,2] | Постійна |
| 38 | [992,31] | Постійна |
| 3 | [1108,38] | Постійна |
Найкоротший шлях між вузлом 15 і будь-яким іншим вузлом визначається починаючи з вузла призначення шляхом проходження їх у зворотному напрямку за допомогою інформації, представленої в постійних мітках. Найкоротший маршрут між вузлами 15 і 3 має таку послідовність вузлів: (3)→ [1108.38] →(38)→ [992.31] →(31)→ [801.21] →(21)→ (15).
Таким чином, одержуємо шлях загальною довжиною 1108 км.
Похожие работы
... зноманітними типами транспортних засобів з урахуванням обмеження на обсяг робот, що можуть виконати транспортні засоби. РОЗДІЛ 3 МАТЕМАТИЧНА МОДЕЛЬ ТРАНСПОРТНОЇ СИСТЕМИ ПІДПРИЄМСТВА 3.1 Структура моделі У якості структурної моделі транспортної системи підприємства можна запропонувати схему, що складається з трьох рівнів. Необхідно відзначити, що з метою деякого спрощення задачі розгляда ...
... ї потужності. У разі зменшення значення функції при деяких параметрах частоти та кількості каналів можна зробити висновок про збільшення впливу завад - збільшення відношення сигнал шум. оптична транспортна інфокомунікаційна мережа Спектральна функція передачі енергії тракту - енергетичний коефіцієнт передачі у такій інтерпретації є фактично функцією перехресних завад - перерозподілу енергії у ...
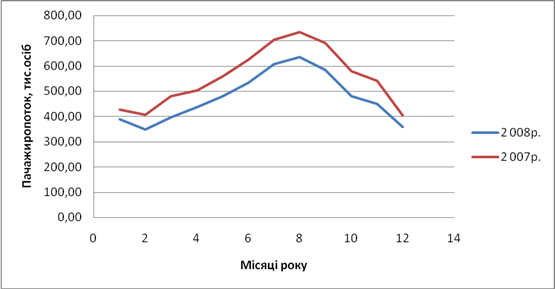
... рентабельність діяльності на 19,92%; збільшення тарифів на 20,86%; зменшення собівартості на 12,51%. Висновки і пропозиції В даній роботі розглянуто пасажирські перевезення транспортного підприємства: ДП МА» Бориспіль» впродовж 2008 року. На протязі періоду підприємство зберігає високий рівень фінансової незалежності й зазначений показник зростає – у 2007 році коефіцієнт фінансової ...
... фіксованої вершини-витоку (кореня дерева) до решти вершин-стоків графа. 2. Математичні моделі потоків заявок та процесів обслуговування у мережах зв'язку мережа зв'язок математичний заявка Окрім структури, математична модель мережі зв'язку повинна описувати потоки заявок та їх обслуговування у мережі. Ці процеси мають стохастичний характер. Розглянемо їх математичні моделі, що будуються на ...
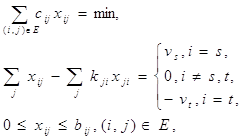


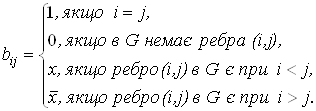
0 комментариев