Задача про максимальний потік (алгоритм Форда-Фалкерсона)

Теоретичні положення з організації моделювання транспортних мереж Задача про максимальний потік (алгоритм Форда-Фалкерсона)

31231

знак

таблиц

изображения

Теоретичні положення з організації моделювання транспортних мереж

4. Задача про максимальний потік (алгоритм Форда-Фалкерсона)

Рішення задачі складається з підготовчого етапу і кінцевого числа кроків, на кожнім з яких відбувається припустиме збільшення потоку. На підготовчому етапі формується матриця пропускних здатностей дуг мережі.

Таблиця 4.1. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	10	¹⁰	10^-
12	7	-	7			7	7
2	¹³	13	-	13	13		13
21	18⁺		18	-	18^-
31			22	22⁺	-		22	22^-
23		22				-	22	22	22
22		21	21		21	21	-	21	21
38					28⁺	28	28	-	28^-
3						7	7	7⁺	-

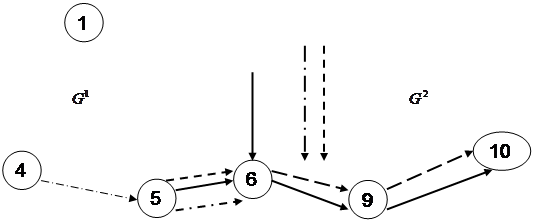
По табл. 4.1. знаходимо шлях l1=(15,21,31,38) зі станції 15 у 3 з позитивною пропускною здатністю. Елементи цього шляху позначаємо знаком «мінус», а симетричні – знаком «плюс». Визначаємо пропускну здатність знайденого шляху, що дорівнює найменшій з пропускних здатностей дуг: C1= min {10,18,22,28}=10.

Визначаються залишкові пропускні здатності дуг знайденого шляху і симетричних йому дуг. Для цього з елементів табл. 4.1. віднімаємо , а до елементів додаємо . У результаті одержимо нову табл. 4.2 зі зміненими пропускними здатностями.

Таблиця 4.2. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	10	10^-	0
12	7	-	7			7	7
2	13⁺	¹³	-	¹³	¹³		13^-
21	28		18	-	8
31			22	32	-		22	12
23		22				-	22	22	22
22		21	21⁺		21	21	-	21	21^-
38					38	28	28	-	18
3						7	7⁺	17	-

Позначаємо стовпці табл. 4.2, знаходимо другий шлях l2=(15,2,22) зі станції 15 у 3, і розставляємо знаки. Визначаємо пропускну здатність знайденого шляху, що дорівнює найменшій з пропускних здатностей дуг:

C2= min {10,13,21}=10.

Змінимо пропускні здатності позначених дуг на (табл. 4.3).

Таблиця 4.3. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	10^-	0	0
12	7⁺	-	7			7^-	7
2	²³	¹³	-	¹³	¹³		3
21	28		18	-	8
31			22	32	-		22	12
23		22⁺				-	22	22	22^-
22		21	31		21	21	-	21	11
38					38	28	28	-	18
3						7⁺	17	17	-

Позначивши стовпці знаходимоl3=(15,12,23).

Величина потоку по шляху : C3= min {10,7,22,}=7.

Розрахувавши нові пропускні здатності дуг, приходимо до табл. 4.4.

Таблиця 4.4. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	3^-	0	0
12	14⁺	-	7			0	7^-
2	²³	13	-	13	13		3
21	28		18	-	8
31			22	32	-		22	12
23		29				-	22	22	15
22		21⁺	31		21	21	-	21	11^-
38					38	28	28	-	18
3						14	17⁺	17	-

Позначивши стовпці знаходимоl4=(15,12,22).

Величина потоку по шляхуl4: C4= min {3,7,11}=3.

Розрахувавши нові пропускні здатності дуг, приходимо до табл. 4.5

Таблиця 4.5. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	0	0	0
12	17	-	7			0	4
2	²³	¹³	-	13	13		3
21	28		18	-	8
31			22	32	-		22	12
23		29				-	22	22	15
22		24	31		21	21	-	21	8
38					38	28	28	-	18
3						14	20	17	-

Переглядаючи рядки і позначаючи стовпці переконуємося в тім, що рядок 15 позначити неможливо. Отже, більше не існує жодного шляху з позитивною пропускною здатністю з вершини 15 у вершину 3.

Заключний крок. Віднімаючи з елементів табл. 4.1 відповідні елементи табл. 4.6, одержимо табл. 4.6.

Таблиця 4.6. Матриця пропускних здатностей дуг мережі

	15	12	2	21	31	23	22	38	3
15	-	10	10	10
12	-10	-				7	3
2	-10		-				10
21	-10			-	10
31				-10	-			10
23		-7				-			7
22		-3	-10				-		13
38					-10			-	10
3						-7	-13	-10	-

Позитивні елементи цієї таблиці характеризують величини дугових потоків. Величина максимального потоку дорівнює сумі елементів 15-го рядка табл. 4.1 або сумі елементів 3-го стовпця. Усі дуги розрізу є насиченими.

Транспортну мережу загалом можна розглядати як систему, що складається з неоднорідних пристроїв або елементів різної складності, що взаємодіють з транспортними потоками потягів, автомобілів, літаків і т.д.

Встановлений окремо для кожної лінії оптимальний план розвитку не завжди доцільний, з огляду на її взаємодію з усією мережею, а іноді навіть практично не може бути реалізований. Зміна технічного оснащення однієї лінії вимагає економічно раціонального перерозподілу потоків на мережі. Отже, одночасно з розвитком пропускної здатності необхідно визначити оптимальний потік, що направляється на лінію, у кожний рік її експлуатації.

Деякі способи посилення пропускної здатності в той або інший конкретний плановий період виявляються найбільш ефективними на значному числі ліній. Найчастіше це ті способи, що безпосередньо зв'язані з реалізацією основних напрямків технічного прогресу на транспорті. Здійснення їх жадає від народного господарства значної витрати тих або інших ресурсів, від чого різко зростає дефіцит останніх. Таким чином, плануючи терміни посилення ліній, необхідно враховувати обмеженість матеріальних і грошових ресурсів, виділюваних на переоснащення залізничного транспорту. Це ставить на чергу задачу оптимізації розвитку пропускної здатності сукупності декількох ліній або навіть мережі в цілому. Вирішити неї в першому наближенні можна оптимізацією розвитку окремих локалізованих систем – груп ліній з однотипними найбільш ймовірними способами посилення пропускної здатності, а також ліній, зв'язаних загальним вантажопотоком, що розподіляється по них у залежності від рівня технічного оснащення.

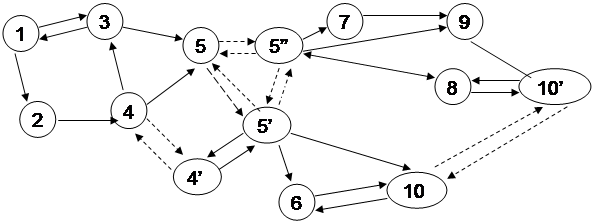
Як видно, деякі ділянки мережі завантажені цілком, а деякі не задіяні в перевізному процесі взагалі. Виходом зі сформованої ситуації, для даної транспортної системи, є підвищення пропускних здатностей таких ліній: 10–7 і 10–15. Ще одним способом зменшення навантаження на дані ділянки може стати розподіл загального обсягу перевезень між залізничним і автомобільним транспортом у місцевому повідомленні (якщо сумарні приведені витрати на транспортування автомобільним транспортом не перевищують витрати на транспортування залізничним транспортом). Дані заходи до деякої міри «розвантажать» напружені ділянки і ділянки, що лімітують, транспортної мережі.

Література

1. Моделирование транспортных систем. Персианов В.А., Скалов К.Ю., Усков Н.С., М-изд-во «Транспорт» 1992 г., – 209 с.

2. Нелинейные сетевые транспортные задачи. Левит Б.Ю., Лившиц В.Н. Институт комплексных транспортных проблем. Изд-во «Транспорт», 2002 – 257 с.

3. Левин Д.Ю. Оптимизация потоков поездов. – М.: Транспорт, 1988. – 175 с.

4. Хорафас Д.Н. Системы и моделирование. Перевод с англ. Изд-во «Мир», М., 1967.

5. Хейт Ф. Математическая теория транспортных потоков. Перевод с англ. Изд-во «Мир», М., 1966.

6. Нестеров Е.П. Транспортные задачи линейного программирования. М.: Изд-во «Транспорт», – 1971.

Теоретичні положення з організації моделювання транспортних мереж

Раздел: Транспорт
Количество знаков с пробелами: 31231
Количество таблиц: 14
Количество изображений: 4

Скачать

... зноманітними типами транспортних засобів з урахуванням обмеження на обсяг робот, що можуть виконати транспортні засоби. РОЗДІЛ 3 МАТЕМАТИЧНА МОДЕЛЬ ТРАНСПОРТНОЇ СИСТЕМИ ПІДПРИЄМСТВА 3.1 Структура моделі У якості структурної моделі транспортної системи підприємства можна запропонувати схему, що складається з трьох рівнів. Необхідно відзначити, що з метою деякого спрощення задачі розгляда ...

Скачать

... ї потужності. У разі зменшення значення функції при деяких параметрах частоти та кількості каналів можна зробити висновок про збільшення впливу завад - збільшення відношення сигнал шум. оптична транспортна інфокомунікаційна мережа Спектральна функція передачі енергії тракту - енергетичний коефіцієнт передачі у такій інтерпретації є фактично функцією перехресних завад - перерозподілу енергії у ...

Скачать

... рентабельність діяльності на 19,92%; збільшення тарифів на 20,86%; зменшення собівартості на 12,51%. Висновки і пропозиції В даній роботі розглянуто пасажирські перевезення транспортного підприємства: ДП МА» Бориспіль» впродовж 2008 року. На протязі періоду підприємство зберігає високий рівень фінансової незалежності й зазначений показник зростає – у 2007 році коефіцієнт фінансової ...

Скачать

... фіксованої вершини-витоку (кореня дерева) до решти вершин-стоків графа. 2. Математичні моделі потоків заявок та процесів обслуговування у мережах зв'язку мережа зв'язок математичний заявка Окрім структури, математична модель мережі зв'язку повинна описувати потоки заявок та їх обслуговування у мережі. Ці процеси мають стохастичний характер. Розглянемо їх математичні моделі, що будуються на ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями

	15	12	2	21	31	23	22	38	3
15	-	10	10	10
12	-10	-				7	3
2	-10		-				10
21	-10			-	10
31				-10	-			10
23		-7				-			7
22		-3	-10				-		13
38					-10			-	10
3						-7	-13	-10	-

	15	12	2	21	31	23	22	38	3
15	-	10	10	10
12	-10	-				7	3
2	-10		-				10
21	-10			-	10
31				-10	-			10
23		-7				-			7
22		-3	-10				-		13
38					-10			-	10
3						-7	-13	-10	-

	15	12	2	21	31	23	22	38	3
15	-	10	10	10
12	-10	-				7	3
2	-10		-				10
21	-10			-	10
31				-10	-			10
23		-7				-			7
22		-3	-10				-		13
38					-10			-	10
3						-7	-13	-10	-