МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ МОДУЛЬНЫХ СИСТЕМ ОБРАБОТКИ ДАННЫХ
Модели и методы решения задач дискретного программирования при проектировании систем обработки данных
На основе выбранного значения оценок вычисляются допустимые решения;
Постановка задачи исследования
Общая постановка блочно-симметричных задач дискретного программирования
Декомпозиция прикладных задач и исходных документов систем обработки данных на этапе технического проектирования
Проектирование модульных блок-схем систем обработки данных
Частные задачи проектирования модульных блок-схем систем обработки данных
Эффективный алгоритм решения блочно-симметричных задач проектирования модульных блок-схем обработки данных
Постановка и решение многокритериальных задач разработки модульных блок-схем обработки данных
Кульба В.В., Мамиконов А.Г. Синтез оптимальных модульных СОД.М.:Наука, 1986
Навигация
На основе выбранного значения оценок вычисляются допустимые решения;
Блочно-симметричные модели и методы проектирования систем обработки данных
158931
знак
0
таблиц
1
изображение
3. На основе выбранного значения оценок вычисляются допустимые решения;
4. Итерационный процесс ветвления по заданному правилу и вычисление оценок продолжается до тех пор, пока не будет получено оптимальное решение.
Идея метода отсечений заключается в следующем. Решается исходная задача. Если полученное решение удовлетворяет условию целочисленности, то задача решена. В противном случае к ограничениям исходной задачи добавляется новое линейное ограничение. Далее решается задача с дополнительно введенным ограничением. Итеративный процесс повторяется, до тех пор, пока не будет получено целочисленное решение.
Примерами успешной реализации методов отсечения являются алгоритмы Гомори [83] .
Вместе с тем, следует отметить ограниченное использование точных методов для решения прикладных задач большой размерности. Несмотря на использование мощных вычислительных систем с большой памятью, совершенствование и развитие математического аппарата «проклятье дискретности» остается и на сегодняшний день.
Поэтому для эффективного решения прикладных задач и преодоления вычислительной сложности точных методов возникла необходимость разработки приближенных и эвристических методов, которые тесно связаны со структурой и особенностями постановки этих задач.
В отличие от точных методов, приближенные позволили решать задачи большой размерности и полученные решения удовлетворяют потребностям практики. При этом в ряде случаев появилась возможность оценить отклонение от оптимального решения либо определить ближайшие окрестности от оптимального решения.
Все это позволило использовать приближенные методы в качестве эффективного инструментария для решения практических задач.
В ряде случаев при проектировании систем обработки данных необходимо учитывать вектор критериев, которые могут противоречить друг другу. Такие постановки задач сводятся к многокритериальным задачам дискретного программирования.
Математическая постановка 
– критериальной задачи предпологает, что задано множество допустимых решений 
, на котором определена векторная целевая функция (ВЦФ) [98,99].
,(1.2.4)
Причем критерии ВЦФ считаем минимизируемыми:
Fv(x)→min, v=1,2,…,N.(1.2.5)
Элемент 
называется Парето-оптимальным, если не существует такого допустимого решения 
, что выполняются неравенства 
, v=1, 2,…, N, среди которых хотя бы одно является строгим.
Через 
обозначаем паретовское множество (ПМ), состоящее из всех Парето-оптимальных элементов рассматриваемой задачи с ВЦФ (1) на множестве 
. Эта задача называется дискретной, если мощность 
множества ее допустимых решений конечна.
Первоначальная формулировка проблемы многокритериальной (векторной) оптимизации восходит к [98, 99] и состоит в нахождении одного или всех элементов ПМ . Заметим, что в однокритериальном случае (
) ПМ представляет собой множество всех оптимумов данной оптимизационной задачи. Для последней, однако, более естественной является проблема нахождения какого-либо («первого попавшегося») оптимума. Как обобщение этой проблемы для многокритериального случая в настоящей работе в качестве основной рассматриваем проблему нахождения полного множества альтернатив (ПМА). Подмножество 
назовем ПМА, если оно удовлетворяет двум условиям: его мощность 
минимально и выполняется 
, где 
, где
.
Множество и 
будем называть множествами альтернатив (МА). В литературе наряду с МА изучается и другие подмножество паретовского множества.
В системном моделировании, в частности, в теорий выбора и принятия решений наиболее распространенными способами нахождения МА являются следующие.
1. Построение (определение) детерминированного формального механизма, позволяющего генерировать альтернативы с помощью параметров алгоритма или с помощью параметров формулы . [100-103]
2. Представление МА в неявном виде с помощью системы соотношений (ограничений ). [104-105]
3. Перечисление всех элементов МА, т.е. представление каждого элемента МА в явном виде. [108, 109]
В работе [121], именно в контексте алгоритмической проблемы, относящейся к последнему из указанных выше трех способов, осуществляется обоснование оценок мощности МА для таких многокритериальных дискретных задач, как задачи о совершенных паросочетаниях, о коммивояжере, о цепях между парой вершин и другие при этом нахождение МА понимается как перечисления с предъявлением всех его элементов [110, 100]. При определенных условиях нижние оценки мощности ПМ и ПМА перечисленных задач оказывается экспоненциальным. Последнее означает, что для рассматриваемых задач проблема нахождения МА является труднорешаемой [110,111]. Или (в терминологии [112,113]) она имеет экспоненциальную вычислительную сложность.
Следуя, [112], рассматриваемую - критериальную задачу назовем индивидуальной, если все ее параметры имеют фиксированные значения. Говорим о массовой - критериальной задаче или, коротко, о задаче, если для некоторых параметров заданы не фиксированные значения, а диапазоны их изменения.
Анализируя приложения той или другой задачи, нетрудно убедиться, что состав критериев ВЦФ обычно меняется. Например, в системах автоматизированного проектирования электронной техники [114-118] возникает многокритериальные задачи на графах, в которых остовное дерево (связывающая сеть) может оценивается такими критериями, как вес, «узкое место» (минимаксный критерий), степень, диаметр и т.д. [119,120]. При этом по мере необходимости эти критерии входят в состав ВЦФ в разнообразных комбинациях, порождая различные варианты задач об остовных деревьях. Общим у этих задач является лишь множество допустимых решений , каждый элемент 
которого является связным остовным подграфом данного графа.
Используя понятие «задача» как переменное, употребляем для ее обозначения символ 
[120]. Конкретизируя рассматриваемую задачу, т.е. определяя для нее множество допустимых решений , присваиваем ей общепринятое наименование и собственное, отличающее её от других задач, обозначение 
.
Перечислим рассматриваемые здесь дискретные многокритериальные задачи:
1. 
- задача о совершенных паросочетаниях, в которой - совершенное паросочетание графа 
с четным числом вершин 
;
2. 
- задача об остовных деревьях, - остовное дерево связного -вершинного графа;
3. 
- задача о цепях, - простая цепь между выделенной парой вершин 
графа 
;
4. 
- задача о коммивояжере, - гамильтонов цикл в -вершинном графе;
5. 
- задача о покрытии -вершинного графа цепями, - остовной подграф, компонентами связности которого являются простые цепи, причем покрытие может представлять собой либо совершенное паросочетание, либо трисочетание, либо состоять из 2- и 3-вершинных цепей.
6. 
- задача о назначениях, т.е. задача о совершенных паросочетаниях на двудольном графе 
, 
, - совершенное паросочетание на .
Таким образом, решение многокритериальных задач ДП весьма сложно в вычислительном отношении, о чем свидетельствует результаты исследований.
По мере развития моделей и методов дискретного программирования, постановки новых задач и других приложений появляется необходимость разработки новых подходов моделей и методов решения задач.
Похожие работы
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... . Особо стоит отметить наличие в СЗИ защиты загрузки операционной системы с гибких магнитных дисков и CD-ROM, которая обеспечивает защиту самих средств защиты от "взлома" с использованием специальных технологий. В различных СЗИ существуют программные и аппаратно-программные реализации этой защиты, однако практика показывает, что программная реализация не обеспечивает необходимой стойкости. ...
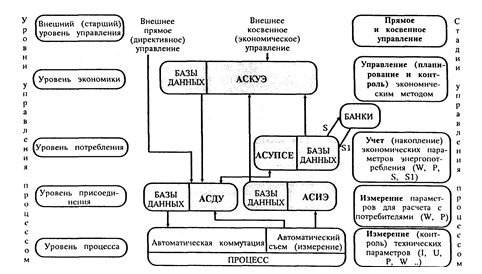
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...
0 комментариев