МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ МОДУЛЬНЫХ СИСТЕМ ОБРАБОТКИ ДАННЫХ
Модели и методы решения задач дискретного программирования при проектировании систем обработки данных
На основе выбранного значения оценок вычисляются допустимые решения;
Постановка задачи исследования
Общая постановка блочно-симметричных задач дискретного программирования
Декомпозиция прикладных задач и исходных документов систем обработки данных на этапе технического проектирования
Проектирование модульных блок-схем систем обработки данных
Частные задачи проектирования модульных блок-схем систем обработки данных
Эффективный алгоритм решения блочно-симметричных задач проектирования модульных блок-схем обработки данных
Постановка и решение многокритериальных задач разработки модульных блок-схем обработки данных
Кульба В.В., Мамиконов А.Г. Синтез оптимальных модульных СОД.М.:Наука, 1986
Навигация
Общая постановка блочно-симметричных задач дискретного программирования
Блочно-симметричные модели и методы проектирования систем обработки данных
158931
знак
0
таблиц
1
изображение
2.1 Общая постановка блочно-симметричных задач дискретного программирования
Ряд прикладных задач: проектирования модульного программного обеспечения и массивов базы данных информационных систем, распределение программных модулей и массивов базы данных по узлам вычислительных сетей, выбор проектов в условиях ограниченных ресурсов можно сформулировать в виде нового класса задач – блочно-симметричных моделей дискретного программирования. В отличие от традиционных моделей модели этого класса позволяют формулировать задачи с несколькими типами переменных различной природы, проводить декомпозицию сложных задач на блоки с единой целевой функцией и разрабатывать эффективные алгоритмы, имеющие полиномиальную вычислительную сложность.
Рассмотрим общую постановку блочно-симметричных задач дискретного программирования [126, 127].
Постановка задачи. Пусть задано множество объектов 
и множество объектов 
с элементами различных типов, а также взаимосвязи между элементам этих множеств, которые определяются матрицей
, 
,
,
Элементы которой целочисленные и булевы. Необходимо объединить элементы множество 
в непересекающиеся подмножества 
, а элементы множества 
- непересекающейся подмножества 
, таким образом, чтобы доставить экстремум целевой функции 
.
Для формализованной постановки задачи введем следующие переменные. Пусть 
- булева матрица, где 
, если 
-й элемент распределяется в 
-ю группу, 
в противном случае. Аналогично 
, где 
, если 
-й элемент распределяется в 
-ю группу и 
в противном случае. В общем случае матрицы переменных 
и 
могут быть целочисленными [136].
Определим на множестве 
функцию 
, зависящую от распределения элементов множеств и по подмножествам 
и 
. Соответственно на множестве - функции 
, а на множестве - функции 
, определяющие ограничения на множествах и .
Блочно-симметричная задача дискретного программирования формулируется следующим образом:
,(2.1.1)
при ограничениях
(2.1.2)
(2.1.3)
В множестве ограничений (2.1.2) и (2.1.3) в зависимости от постановок задач знаки неравенств могут меняться на противоположеные.
В общем случае двухиндексные матрицы – переменных и и заданная матрица 
могут быть целочисленными.
Рассмотрим задачу при условии, когда переменные , и - булевы матрицы. В качестве функции часто используют функцию вида 
, где
(2.1.4)
Рассмотрим выражение (2.1.4), которое представляет собой произведение матриц переменных и и заданной матрицы , на которой определена целевая функция. В отличие от традиционных постановок задач дискретного программирования в данной постановке имеются два типа переменных и , переменные и симметричны относительно заданной матрицы .
В задаче (2.1.1) -(2.1.3) можно выделить множество ограничений вида (2.1.2), которые зависят от переменной , и множество ограничений вида (2.1.3), которые зависят от переменной .
Функционал вида можно представить следующим образом:
(2.1.5)
(2.1.6)
(2.1.7)
(2.1.8)
(2.1.9)
В постановке задачи (2.1.5) - (2.1.9) выделим блок функции (2.1.6), (2.1.7), зависящий только от переменной , и блок функций (2.1.8), (2.1.9), зависящий только от переменной , объединенных единым функционалом вида (2.1.5). Заметим, что в ряде постановок задач может быть блок ограничений вида
(2.1.10)
зависящий от переменных и .
В этом случае можно выделить блок функционала цели вида (2.1.5), (2.1.10).
Отсюда следует.
Определение 2.1. Блочно-симметричной задачей дискретного программирования назовем задачу вида (2.1.5) - (2.1.9), где переменные и и значения функций 
, 
, 
- целые, либо булевые
Рассмотрим выражение (2.1.4). из него следует что переменные и симметричны относительно заданной матрицы и функция (2.1.4) может быть определена как слева направо, так и наоборот, т.е.
(2.1.11)
На основе общей постановки определим основные свойства сформулированного класса задач, отличающие его от традиционных постановок задач дискретного программирования.
Свойство 1. В блочно-симметричной задаче имеется два типа переменных и различного содержания, определенных как целочисленные (булевы) матрицы на заданной матрице .
В общем случае переменных может быть и больше в зависимости от постановок задач.
Свойство 2. Блочность задачи заключается в выделении в постановке отдельных блоков функций вида (2.1.5), (2.1.10); (2.1.6), (2.1.7) и (2.1.8), (2.1.9), которые соответственно зависят от переменных и .
Как видно из указанных соотношении каждый из блоков имеет свою целевую функцию и координируется общим функционалом вида (2.1.5).
Свойство 3. Блочно-симметричную задачу в большинстве случаев можно представить в матричной форме вида (2.1.11).
Матричная форма постановки блочно-симметричных задач позволяет использовать аппарат теории матриц и разрабатывать эффективные алгоритмы решения задач этого класса.
Свойство 4. Симметричность задачи заключается в возможности вычисления (2.1.11) как слева направо, так и обратном направлении.
Указанные свойства и особенности блочно-симметричных задач ДП позволяют синтезировать алгоритмы, обеспечивающих решение практических задач большой размерности.
В ряде постановок задач функционал (2.1.1) можно представить в виде вектора функций 
. В этом случае формулируется многокритериальная блочно-симметричная задача дискретного программирования.
Анализ постановки, свойств и особенности блочно-симметричных задач позволил разработать и предложить подход и схему метода решения общей задачи на основе следующего утверждения.
Утверждение. Распределение элементов множества по непересекающим подмножествам соответствует логическому сложению строк матриц 
, а распределение элементов множества по непересекающимся подмножествам - логическому сложению столбцов матрицы . [132, 133] Результаты данного утверждения позволяют просто вычислить оценки и направления поиска решения для разработки эффективных алгоритмов.
Введем понятие базиса решения задач. Под базисом понимается заранее заданный состав элементов подмножеств и .
В матрице базис находится как некоторая матрица 
элементы которых определены. Данную матрицу путем перестановки номеров строки столбцов матрицы и их перенумировки всегда можно определить в левом верхнем углу. Такое представление упрощает процедуру оценок и определения направления поиска решения.
Для решения блочно-симметричной задачи дискретного программирования при условии, когда , и - булевы матрицы, разработана и предложена эффективная схема решения задачи. Схема поиска решения состоит из следующих основных этапов:
1. В булевой матрице выделим подматрицу 
, 
, 
и определим её как базис решения задачи.
2. Определим матрицу 
, 
, направления поиска решения путем логического сложения небазисных строк матрицы со строками базиса и вычислим значения оценок только по позициям базиса.
3. В соответствии с полученными оценками осуществим распределение элементов множества по множествам . В результате зафиксируем решение и промежуточную. Матрицу 
, 
, 
.
4. Определим матрицу 
, 
, 
. 
направления поиска решения путем логического сложения небазисных столбцов промежуточной матрицы со столбцами базиса и вычислим значения оценок только по позициям базиса матрицы 
.
5. В соответствии с полученными оценками матрицы распределим элементы множества по множествам. В результате фиксируем решение и целевую матрицу , на которой определено значение целевой функции .
6. Следует отметить, что поиск решения задачи может осуществляться как в прямом направлении по схеме 
, так и в обратном направлении по схеме 
.
При заданном базисе решение данного класса задач имеет полиноминальную вычислительную сложность.
Похожие работы
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... . Особо стоит отметить наличие в СЗИ защиты загрузки операционной системы с гибких магнитных дисков и CD-ROM, которая обеспечивает защиту самих средств защиты от "взлома" с использованием специальных технологий. В различных СЗИ существуют программные и аппаратно-программные реализации этой защиты, однако практика показывает, что программная реализация не обеспечивает необходимой стойкости. ...
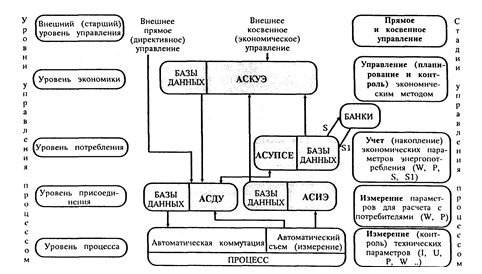
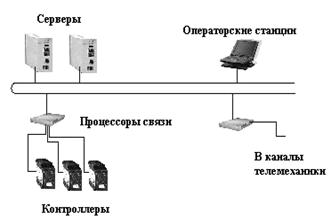
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...
0 комментариев