Навигация
Эффективный алгоритм решения блочно-симметричных задач проектирования модульных блок-схем обработки данных
3.1 Эффективный алгоритм решения блочно-симметричных задач проектирования модульных блок-схем обработки данных
Анализ методов и алгоритмов решения задач дискретного программирования показал, что они, в основном, являются NP-полными и имеют экспоненциальную вычислительную сложность. Следовательно, не могут быть решены задачи большой размерности в различных приложениях [134-137].
В отличие от известных методов и алгоритмов путем анализа и исследования постановки, свойств и особенностей блочно-симметричных задач разработан и предложен эффективный алгоритм решения задач этого класса.
Рассмотрим алгоритм решения блочно-симметричных задач вида (2.2.1)-(2.2.5), (3.2.1)-(3.2.7), а также частных задач [138].
Для описания алгоритма введем следующие понятия.
В случае, если в процессе проектирования модульных блок-схем не заданы число разрабатываемых модулей ![]() и массивов базы данных
и массивов базы данных ![]() , они могуть быть определены и следующих соотношений
, они могуть быть определены и следующих соотношений ![]() ,
, ![]() , где
, где ![]() и
и ![]() соответственно максимальное число процедур в модуле и максимальное число информационных элементов в массивах базы данных. Определим понятие базиса решения задачи.
соответственно максимальное число процедур в модуле и максимальное число информационных элементов в массивах базы данных. Определим понятие базиса решения задачи.
Определение 3.1.1. Подматрицу ![]() , где
, где ![]() ;
; ![]() ;
; ![]() ;
; ![]() , определенную на исходной матрице
, определенную на исходной матрице ![]() , назовем исходным базисом решения задачи.
, назовем исходным базисом решения задачи.
В качестве базиса используются ключевые информационные элементы и используемые ими процедуры обработки данных. Если ключевые информационные элементы не определены, то элементы (строки и столбцы матрицы ![]() ) задаются исходя из технологических требований проекта.
) задаются исходя из технологических требований проекта.
Определение 3.1.2. Величины
![]() (3.1.1)
(3.1.1)
и
![]() (3.1.2)
(3.1.2)
назовём расстоянием между строками (столбцами) не вошедшими в базис и строками (столбцами), которые вошли в базис.
Вычисленные значения величин ![]() и
и ![]() составляют матрицу
составляют матрицу ![]() и
и ![]() . Минимальные значения элементов
. Минимальные значения элементов ![]() и
и ![]() определяютоптимальное однозначное отображение процедур в модули и информационных элементов в массивы базы данных.
определяютоптимальное однозначное отображение процедур в модули и информационных элементов в массивы базы данных.
В процессе отображения с матрицами ![]() и
и ![]() тесно связаны матрицы состояний соответственно
тесно связаны матрицы состояний соответственно ![]() и
и ![]() , указывающие текущее состояние исходной матрицы после операции отображения, которые заключаются в логическом сложении небазисных строк (столбцов) с базисными.
, указывающие текущее состояние исходной матрицы после операции отображения, которые заключаются в логическом сложении небазисных строк (столбцов) с базисными.
Алгоритм состоит из ряда итераций. Поэтому определим его как алгоритм итеративных отображений (АИО). Алгоритм состоит из следующих операций:
1. Ввод матрицы ![]() . Выделение базиса в матрице
. Выделение базиса в матрице ![]() . Переход к 2.
. Переход к 2.
2. Вычислить величины ![]() и составить матрицу
и составить матрицу ![]() . Зафиксировать состояние матрицы
. Зафиксировать состояние матрицы ![]() . Переход к 3.
. Переход к 3.
3. ![]() -я итерация.
-я итерация.
3.1. В матрице найти ![]() - й минимальный элемент
- й минимальный элемент ![]() . При наличии нескольких минимальных элементов, среди них выберем такой элемент, для которого значение суммы элементов по строке максимально. Таким образом, выбирая минимальный элемент, избавляемся от большого число связей. Если элементов такого свойства несколько, то среди этих минимальных элементов выберем элемент расположенный первым от начало отсчета строк. Переход к 3.2.
. При наличии нескольких минимальных элементов, среди них выберем такой элемент, для которого значение суммы элементов по строке максимально. Таким образом, выбирая минимальный элемент, избавляемся от большого число связей. Если элементов такого свойства несколько, то среди этих минимальных элементов выберем элемент расположенный первым от начало отсчета строк. Переход к 3.2.
3.2. Определить элементы ![]() матрицы
матрицы ![]() . Проверить ограничения на число процедур в составе каждого модуля. Если оно неудовлетворительно, то перейти к 3.3, иначе к 3.1.
. Проверить ограничения на число процедур в составе каждого модуля. Если оно неудовлетворительно, то перейти к 3.3, иначе к 3.1.
3.3. Исключить из рассмотрения элемент ![]() . Установить
. Установить ![]() . Переход к 3.1.
. Переход к 3.1.
3.4. Вычислить состояние матрицы ![]() . Переход к 3.5.
. Переход к 3.5.
3.5. Исключить из рассмотрения строку с номером ![]() . Пересчитать величины
. Пересчитать величины ![]() относительно
относительно ![]() столбца с учетом нового состояния
столбца с учетом нового состояния ![]() . Переход к 3.6.
. Переход к 3.6.
3.6. Проверить условие: все ли процедуры распределены? Если нет, то перейти к следующей итерации, приняв ![]() . Иначе переход к 4
. Иначе переход к 4
4. Запомнить содержание матриц ![]() и
и ![]() . Переход к 5.
. Переход к 5.
5. Вычислить ![]() относительно
относительно ![]() и составить матрицу
и составить матрицу ![]() . Переход к 6.
. Переход к 6.
6. ![]() -я итерация.
-я итерация.
6.1. В матрице ![]() найти
найти ![]() -й минимальный элемент. При наличии нескольких минимальных элементов, среди них выберем такой элемент, для которого значение суммы по строкам минимально. Если элементов такого свойства несколько, то среди этих минимальных элементов выберем элемент расположенный первым от начало отсчета строк. Переход к 6.2.
-й минимальный элемент. При наличии нескольких минимальных элементов, среди них выберем такой элемент, для которого значение суммы по строкам минимально. Если элементов такого свойства несколько, то среди этих минимальных элементов выберем элемент расположенный первым от начало отсчета строк. Переход к 6.2.
6.2. Определить элементы ![]() матрицы
матрицы ![]() . Проверить ограничения на число информационных элементов в логическом массиве. Если оно неудовлетворительно, то перейти к 6.3.
. Проверить ограничения на число информационных элементов в логическом массиве. Если оно неудовлетворительно, то перейти к 6.3.
6.3. Исключить из рассмотрения элемент ![]() . Установить
. Установить ![]() . Переход к 6.1.
. Переход к 6.1.
6.4. Вычислить состояние матрицы ![]() . Переход к 6.5.
. Переход к 6.5.
6.5. Исключить из рассмотрения строку с номером ![]() . Пересчитать величины
. Пересчитать величины ![]() относительно
относительно ![]() столбца с учетом нового состояния
столбца с учетом нового состояния ![]() . Переход к 6.6.
. Переход к 6.6.
6.6. Проверить условие: все ли информационные элементы распределены? Если нет, то перейти к следующей итерации, приняв ![]() . Иначе переход к 7.
. Иначе переход к 7.
7. Вывод решения задачи: матриц ![]() ,
, ![]() ,
, ![]() и значение целевой функции
и значение целевой функции ![]() .
.
Сравним сложность для получения решения с использованием данного алгоритма, оцениваемую общим количеством шагов, с широко известным методом «ветвей и границ» для решения дискретных задач комбинаторного типа.
Необходимые количество шагов в процессе решения задачи с использованием алгоритма итеративных отображений равно
![]() ,(3.1.3)
,(3.1.3)
где ![]() ,
, ![]() - количество итераций в процессе формирования соответствующих решений
- количество итераций в процессе формирования соответствующих решений ![]() и
и ![]() . Число шагов с использованием метода «ветвей и границ» для решения указанных задач определяется по следующей формуле
. Число шагов с использованием метода «ветвей и границ» для решения указанных задач определяется по следующей формуле
![]() .(3.1.4)
.(3.1.4)
Сравнение соотношений (3.1.1), (3.1.2) показывает эффективность и полиномиальную сложность разработанных алгоритмов для решения поставленных задач большой размерности, в отличие от метода «ветвей и границ».
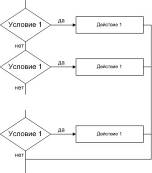
Блок-схема алгоритма итеративных отображений приведена на рис. 3.1.1.
Рассмотрим численный пример решения задачи. Необходимо синтезировать блок-схему модульной СОД, минимизирующую общее число обращений к логическим массивом базы данных.
Задача решается при следующих условиях: допустимое число процедур в составе модуля 3, допустимое число информационных элементов в составе логических массивов 4. Число модулей и логических массивов определяется по формулам: ![]() и
и ![]() , с округлением в большую строку.
, с округлением в большую строку.
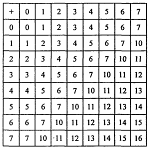
В таблице 3.1.1 представлена исходная матрица ![]() с выделенным базисом
с выделенным базисом ![]() в верхнем левом углу исходной матрицы. В базис вошли 1, 2, 3, 4, 5 и строки 1, 2, 3 матрицы
в верхнем левом углу исходной матрицы. В базис вошли 1, 2, 3, 4, 5 и строки 1, 2, 3 матрицы ![]() . На рисунке 3.1.2 показан процесс формирования решения
. На рисунке 3.1.2 показан процесс формирования решения ![]() с использованием разработанного алгоритма. Матрица
с использованием разработанного алгоритма. Матрица ![]() определена с использованием соотношения (3.1.1).
определена с использованием соотношения (3.1.1).
Процесс отображений представлен таблицей, в которой приведены номер итерации ![]() , минимальный элемент из
, минимальный элемент из ![]() , в соответствии с которым отображается номер процедуры
, в соответствии с которым отображается номер процедуры ![]() в номер модуля
в номер модуля ![]() . На рисунке представлены матрицы
. На рисунке представлены матрицы ![]() и
и ![]() , содержание которых определено базисом поиска решения
, содержание которых определено базисом поиска решения ![]() , а в правой матрице
, а в правой матрице ![]() и
и ![]() , полученные с использованием алгоритма итеративных отображений.
, полученные с использованием алгоритма итеративных отображений.
На рисунке 3.1.2 показан процесс формирования решения ![]() . Матрица
. Матрица ![]() определена с использованием соотношения (3.1.2) и матрицы
определена с использованием соотношения (3.1.2) и матрицы ![]() . Процесс отображения представлен таблицей, в которой приведены номер итерации
. Процесс отображения представлен таблицей, в которой приведены номер итерации ![]() , минимальный элемент
, минимальный элемент ![]() из
из ![]() в соответствии с которым номер информационного элемента
в соответствии с которым номер информационного элемента ![]() отображается в номер файла
отображается в номер файла ![]() . На рисунке 3.1.2 представлена матрица
. На рисунке 3.1.2 представлена матрица ![]() , которая сформирована до поиска оптимального решения и определена базисом, а также матрица, полученная в результате формирования решения
, которая сформирована до поиска оптимального решения и определена базисом, а также матрица, полученная в результате формирования решения ![]() . А также представлены матрица решения задачи
. А также представлены матрица решения задачи ![]() , полученная с использоваием алгоритма итеративных отображений, и матрица
, полученная с использоваием алгоритма итеративных отображений, и матрица ![]() , полученная в результате отображения. Матрица
, полученная в результате отображения. Матрица ![]() соответствует матрице целевой функции
соответствует матрице целевой функции ![]() , отражающей взаимосвязи программных модулей и логических масивов базы данных модульной блок-схемы. Оптимальное значение целевой функции, полученное при этом базисе и ограничеиях, равно
, отражающей взаимосвязи программных модулей и логических масивов базы данных модульной блок-схемы. Оптимальное значение целевой функции, полученное при этом базисе и ограничеиях, равно ![]() =
=![]() =6.
=6.
С использованием алгоритма итеративных отображений решаются и частные задачи вида (2.4.1)-(2.4.4) и (2.4.5)-(2.4.8) как части блочно-симметричных задач.
Похожие работы
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... . Особо стоит отметить наличие в СЗИ защиты загрузки операционной системы с гибких магнитных дисков и CD-ROM, которая обеспечивает защиту самих средств защиты от "взлома" с использованием специальных технологий. В различных СЗИ существуют программные и аппаратно-программные реализации этой защиты, однако практика показывает, что программная реализация не обеспечивает необходимой стойкости. ...
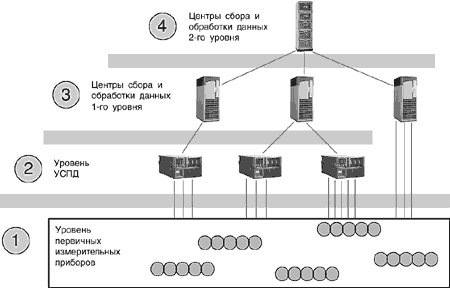
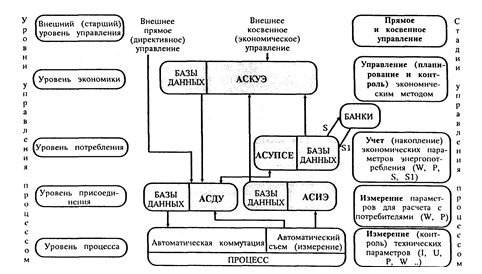
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...


0 комментариев