Навигация
Математическое и статистическое обеспечение выпускной квалификационной работы
4.2 Математическое и статистическое обеспечение выпускной квалификационной работы
Математико-статистическое обеспечение выпускной квалификационной работы опирается на применение различных показателей, таких как средняя арифметическая величина, среднеквадратическое отклонение, коэффициент корреляции и так далее. Рассмотрим более подробно результаты применения этих и других показателей на двух важнейших вопросах, задаваемых респондентам в анкете социологического исследования. Первый вопрос – оценка уровня информированности жителей муниципального образования "Нижнекамский муниципальный район" о деятельности местных органов власти, и второй вопрос, по уровню доверия населения к местным органам власти и управления.
Для подтверждения, или опровержения гипотезы социологического исследования, проведенного автором выпускной квалификационной работы, в расчетах используется метод корреляционного анализа.
Выдвинутая автором гипотеза сформулирована в следующих тезисах:
– участие граждан в деятельности органов местного самоуправления недостаточное (характеризуется равнодушием, безынициативностью населения, боязнью всего нового, в том числе и новых руководителей);
– одной из причин вышеперечисленных явлений, является неумелое, неэффективное использование органами местного самоуправления PR-технологий, отсутствие в пресс-службах специалистов по связям с общественностью;
– недостаточная информированность населения о деятельности местных властей, при наличии потребности населения в данной информации;
– взаимосвязь между уровнем информированности жителей муниципального образования о деятельности местных органов власти и их доверия к ним.
Последнее предположение, о существующей взаимосвязи между уровнем информированности и уровнем доверия к деятельности местных органов власти, проверим с помощью корреляционного анализа.
Данные по уровню информированности граждан о деятельности местных органов власти и доверия к их деятельности, были выявлены с помощью анкетирования населения муниципального образования "Нижнекамский муниципальный район". Расчет выборочной совокупности дан в программе социологического исследования, пункт 4.4 Социологическое обеспечение выпускной квалификационной работы.
Ответы респондентов, проведенного социологического исследования, на вопросы по уровню информированности и доверия к деятельности местных органов власти, отражены в таблице – 2.
Таблица 2 – Распределение ответов на вопросы о информированности и доверии к деятельности местных органов власти
| Вопрос | Вариант ответа | Ответы (в процентах) |
| 1 Ваш уровень осведомленности о деятельности органов местного самоуправления | а) совсем не информирован | 7,2 |
| б) информирован, но хотел бы знать больше | 58,2 | |
| в) хорошо освещен о деятельности МСУ | 10,5 | |
| г) затрудняюсь ответить | 11 | |
| д) не интересуюсь деятельностью местных органов власти | 13,1 | |
| 2 Доверяете ли Вы органам местной власти | а) совсем не доверяю | 8,5 |
| б) доверяю частично | 68 | |
| в) да, полностью доверяю | 4,5 | |
| г) затрудняюсь ответить | 6 | |
| д) мне безразлична их деятельность | 13 |
Корреляционный метод – один из экономико-математических методов исследования, позволяющий определить количественную взаимосвязь между несколькими явлениями исследуемой системы. Корреляционная зависимость в отличие от функциональной может проявляться только в общем, среднем случае, то есть в массе случаев – наблюдений. Поэтому корреляция представляет собой вероятностную зависимость между явлениями, при которой средняя величина параметров одного из них изменяется в зависимости от других [8, с. 232].
Основными задачами при изучении корреляционных зависимостей является: отыскание математической формулы, которая бы выражала эту зависимость X от Y; измерение тесноты такой зависимости.
Прямолинейное уравнение регрессии, выражено в функции (1):
![]() =
= ![]() +
+![]() *
*![]() , (1)
, (1)
где ![]() – параметр уравнения, которые рассчитываются по формуле (2);
– параметр уравнения, которые рассчитываются по формуле (2);
![]() – параметр уравнения, который рассчитывается по формуле (3).
– параметр уравнения, который рассчитывается по формуле (3).
Рассмотрим эти формулы и рассчитаем их значения.
![]() = ,
= , 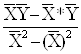 , (2)
, (2)
где ![]() – среднее значение переменной
– среднее значение переменной ![]() ;
;
![]() – среднее значение переменной
– среднее значение переменной ![]() ;
;
![]() – среднее значение квадрата переменной
– среднее значение квадрата переменной ![]() ;
;
![]() – среднее значение
– среднее значение ![]() переменной в квадрате.
переменной в квадрате.
Рассмотрим формулу (3) расчета переменной ![]() .
.
![]() =
= ![]() –
– ![]() *
*![]() , (3)
, (3)
где, ![]() – среднее значение переменной
– среднее значение переменной ![]() ;
;
![]() – параметр уравнения, который находится по формуле (2);
– параметр уравнения, который находится по формуле (2);
![]() – среднее значение переменной
– среднее значение переменной ![]() .
.
Расчеты для нахождения значений по формуле (2) и по формуле (3) приведены в таблице 3.
Таблица 3 – Расчеты уравнения регрессии
| Рассчитанные значения показателей | ||||
| Y | X | XY | X2 | Y2 |
| 68 | 58,2 | 3957,6 | 3387,24 | 4624 |
| 13 | 13,1 | 170,3 | 171,61 | 169 |
| 6 | 11 | 66 | 121 | 36 |
| 4,5 | 10,5 | 47,25 | 110,25 | 20,25 |
| 8,5 | 7,2 | 61,2 | 440,64 | 72,25 |
| ∑ 100 | ∑ 100 | ∑ 4302,35 | ∑ 4230,74 | ∑ 4921,5 |
Таким образом, рассчитав все необходимые расчеты в таблице, рассчитаем неизвестные показатели.
![]() = (860,47 – 20*20)/(846,15 – 20*20) = 460,47/446,15 = 1,03;
= (860,47 – 20*20)/(846,15 – 20*20) = 460,47/446,15 = 1,03;
![]() = 20 – 1,03*20 = 20-20,6 = – 0,6;
= 20 – 1,03*20 = 20-20,6 = – 0,6;
![]()
![]() = 4302,35/5 = 860,47;
= 4302,35/5 = 860,47;
![]() = 4230,74/5 = 846,15;
= 4230,74/5 = 846,15;
![]() = 4921,5/5 = 984,3.
= 4921,5/5 = 984,3.
Подставив полученные значения параметров ![]() и
и ![]() в уравнение регрессии, получим следующее уравнение:
в уравнение регрессии, получим следующее уравнение: ![]() = – 0,6 + 1,03*
= – 0,6 + 1,03*![]() .
.
Для измерения тесноты зависимости между ![]() и
и ![]() , воспользуемся линейным коэффициентом корреляции, рассчитываемая по формуле (4).
, воспользуемся линейным коэффициентом корреляции, рассчитываемая по формуле (4).
r =![]() , (4)
, (4)
где ![]() – среднее квадратическое отклонение в ряду х;
– среднее квадратическое отклонение в ряду х;
![]() – среднее квадратическое отклонение в ряду у.
– среднее квадратическое отклонение в ряду у.
Рассчитаем среднее квадратическое отклонение показателей х и у, по формулам (5) и (6), соответственно.
![]() =
= ![]() , (5)
, (5)
Все значения параметров формулы уже найдены, подставим их в формулу для расчета. Итак, среднее квадратическое отклонение
![]() =
=![]() = 21,12.
= 21,12.
Те же вычисления проведем для расчета ![]() , вычисляемая по формуле (6).
, вычисляемая по формуле (6).
![]() =
= ![]() , (6)
, (6)
Подставим значения из таблицы 6 и получим![]() =
= ![]() = 24,17.
= 24,17.
Подставим найденные значения средних квадратических отклонений ![]() и
и ![]() в уравнение линейного коэффициента корреляции. Получим следующее значение r = (860,47 – 20*20)/(21,12*24,17) = 460,47/510,47 = 0,902.
в уравнение линейного коэффициента корреляции. Получим следующее значение r = (860,47 – 20*20)/(21,12*24,17) = 460,47/510,47 = 0,902.
Чем ближе рассчитываемый коэффициент корреляции к плюс единице (при прямой зависимости), и к минус единице (при обратной зависимости), тем выше теснота связи. Соответственно при коэффициентах корреляции равной 0,902 мы можем констатировать, очень тесную связь между показателями информированности респондентов о деятельности местного самоуправления и их доверием к местным властям.
При расчете коэффициента корреляции, особенно если он исчислен для небольшого числа наблюдений, очень важно оценить его надежность (значимость). Для этого рассчитаем среднюю ошибку коэффициента корреляции, по формуле (7).
![]() , (7)
, (7)
где ![]() – число степеней свободы при линейной зависимости.
– число степеней свободы при линейной зависимости.
Найдем также отношение коэффициента корреляции к его средней ошибке, то есть t, по формуле (8). Этот показатель сравнивается с табличным значением t-критерия Стьюдента.
t ![]() (8)
(8)
Подставим уже найденные значения параметров в формулы.
![]() = (1 – (0,902)2/
= (1 – (0,902)2/![]() = 0,107;
= 0,107;
t расчетное = r/![]() = 0,902/0,107 = 8,49.
= 0,902/0,107 = 8,49.
По таблице Стьюдента, находим, что при числе степеней свободы k равное 3 (5 – 2 = 3), и ![]() равное 0,05, табличное (критическое, пороговое) t равно 3,18.
равное 0,05, табличное (критическое, пороговое) t равно 3,18.
Поскольку фактическое (расчетное) t больше табличного (8,49 больше, числа 3,18), то линейный коэффициент корреляции r равный 0,902 считается значимым, а связь между ![]() и
и ![]() – реальной.
– реальной.
Следовательно, с помощью статистических расчетов и анализа данных, автором установлена сильная корреляционная зависимость показателей уровня информированности опрошенных респондентов и уровня доверия их к местным органам власти.
Похожие работы
... общественных связей выполняется государственными информационными агентствами, управлениями по связям с общественностью, ответственными лицами по связям с прессой и другими подразделениями местных органов власти. Функциональные особенности деятельности пресс-служб в органах государственной власти определяют их организационное устройство. Как показывает практика, чаще всего отделы, которые в ...
... формированию активного имиджа главы муниципального образования, по снижению применяемых манипуляций и более близкому взаимодействию населения и власти. 3 Основные рекомендации и предложения по формированию активного имиджа главы муниципального образования 3.1 Взаимодействие населения с местным органом власти как технология формирования имиджа Активный имидж власти предполагает активное ...
... Если на содержание постоянного отдела ПР есть возможность выделить лишь незначительную сумму, имеет смысл обратиться к консультативному агентству, а не создавать собственный отдел. 2.2 Специфика работы пресс-службы в банковской системе Русфинбанк В России сегодня практически каждый государственный орган имеет собственную службу по связям с общественностью в виде пресс-службы, пресс-центра, ...
... к деятельности какого ведомства они относятся. Для Питкярантского района характерен именно сферный тип социальной политики с элементами демографического типа. 1.2. Современный подход к решению вопросов социальной политики в городе и районе. Местное самоуправление в системе государственных и муниципальных органов призвано обеспечивать комплексное решение вопросов обслуживания населения, ...




0 комментариев