Навигация
Складемо симплексну таблицю для першого опорного плану задачі
2. Складемо симплексну таблицю для першого опорного плану задачі.
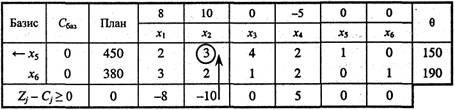
Елементи останнього рядка симплекс-таблиці є оцінками Δj, за допомогою яких опорний план перевіряють на оптимальність. їх визначають так:
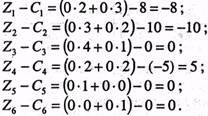
У стовпчику «План» оцінкового рядка записують значення цільової функції Z, якого вона набуває для визначеного опорного плану:![]() =0-450 + 0-380 = 0.
=0-450 + 0-380 = 0.
3. Після обчислення всіх оцінок опорний план перевіряють на оптимальність. Для цього продивляються елементи оцінкового рядка. Якщо всі ![]() (для задачі на max) або
(для задачі на max) або ![]() (для задачі на min), визначений опорний план є оптимальним. Якщо ж в оцінковому рядку присутня хоча б одна оцінка, що не задовольняє умову оптималь-ності (від'ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним і його можна поліпшити.
(для задачі на min), визначений опорний план є оптимальним. Якщо ж в оцінковому рядку присутня хоча б одна оцінка, що не задовольняє умову оптималь-ності (від'ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним і його можна поліпшити.
У цій задачі в оцінковому рядку дві оцінки ![]() та
та ![]() суперечать умові оптимальності, і тому перший визначений опорний план є неоптимальним. За алгоритмом симплекс-методу необхідно від нього перейти до іншого опорного плану задачі.
суперечать умові оптимальності, і тому перший визначений опорний план є неоптимальним. За алгоритмом симплекс-методу необхідно від нього перейти до іншого опорного плану задачі.
4. Перехід від одного опорного плану до іншого виконують зміною базису, тобто за рахунок виключення з поточного базису якоїсь змінної та включення замість неї нової з числа вільних змінних.
Для введення до нового базису беремо змінну![]() , оскільки їй відповідає найбільша за абсолютною величиною оцінка серед тих, які не задовольняють умову оптимальності (
, оскільки їй відповідає найбільша за абсолютною величиною оцінка серед тих, які не задовольняють умову оптимальності (![]() ).
).
Щоб визначити змінну, яка підлягає виключенню з поточного базису, для всіх додатних елементів стовпчика «х2» знаходимо відношення ![]() і вибираємо найменше значення. Згідно з даними симплексної таблиці бачимо, що min
і вибираємо найменше значення. Згідно з даними симплексної таблиці бачимо, що min![]() , і тому з базису виключаємо змінну
, і тому з базису виключаємо змінну![]() , а число
, а число![]() = 3 називатимемо розв'язувальним елементом. Подальший перехід до нового опорного плану задачі полягає в побудові наступної симплексної таблиці, елементи якої розраховують за методом Жордана—Гаусса.
= 3 називатимемо розв'язувальним елементом. Подальший перехід до нового опорного плану задачі полягає в побудові наступної симплексної таблиці, елементи якої розраховують за методом Жордана—Гаусса.
Друга симплексна таблиця має такий вигляд:
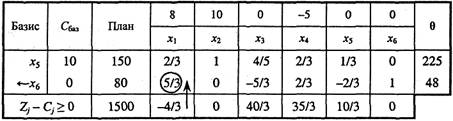
У цій таблиці спочатку заповнюють два перших стовпчики «Базис» і «![]() », а решту елементів нової таблиці розраховують за розглянутими далі правилами:
», а решту елементів нової таблиці розраховують за розглянутими далі правилами:
1. Розв'язувальний (напрямний) рядок необхідно поділити на розв'язувальний елемент і здобуті числа записати у відповідний рядок нової симплексної таблиці.
2. Розв'язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв'язувального елемента.
3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.
4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.
Усі інші елементи наступної симплексної таблиці розраховують за правилом прямокутника.
Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:;
1 — розв'язувальний елемент;
2 — число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;
3 та 4 — елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.
Необхідний елемент нової симплекс-таблиці визначають так:
![]()
Наприклад, визначимо елемент ![]() , який розміщується в новій таблиці в другому рядку стовпчика «Х4». Складемо умовний прямокутник:
, який розміщується в новій таблиці в другому рядку стовпчика «Х4». Складемо умовний прямокутник:
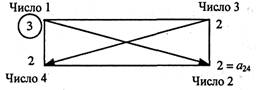
Тоді ![]() = (3-2-2-2):3 = 2/3. Це значення записуємо в стовпчик «
= (3-2-2-2):3 = 2/3. Це значення записуємо в стовпчик «![]() » другого рядка другої симплексної таблиці.
» другого рядка другої симплексної таблиці.
Аналогічно розраховують усі елементи нової симплексної таблиці, у тому числі елементи стовпчика «План» та оцінкового рядка. Наявність двох способів визначення оцінок опорного плану (за правилом прямокутника та за відповідною формулою) дає змогу контролювати правильність арифметичних обчислень на кожному кроці симплекс-методу.
Після заповнення нового оцінкового рядка перевіряємо виконання умови оптимальності ![]() для другого опорного плану. Цей план також неоптимальний, оскільки
для другого опорного плану. Цей план також неоптимальний, оскільки ![]() . Використовуючи процедуру симплекс-методу, визначаємо третій опорний план задачі, який наведено у вигляді таблиці:
. Використовуючи процедуру симплекс-методу, визначаємо третій опорний план задачі, який наведено у вигляді таблиці:
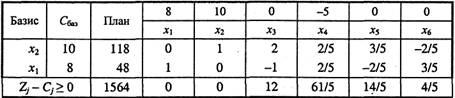
В оцінковому рядку третьої симплексної таблиці немає від'ємних чисел, тобто всі ![]() і задовольняють умову оптимальності. Це означає, Що знайдено оптимальний план задачі:
і задовольняють умову оптимальності. Це означає, Що знайдено оптимальний план задачі:
![]()
Або
![]()
Отже, план виробництва продукції, що передбачає випуск 48 одиниць продукції А та 118 од. продукції В, оптимальний і дає найбільший прибуток 1564 дол. При цьому час роботи верстатів використовується повністю (х5 = х6 = 0).
Задачу можна розв'язати симплекс-методом, узявши не три симплексні таблиці, а одну, в якій послідовно записувати всі ітерації.
Задача 2.42.
Розв'язати задачу 2.41 із додатковою умовою: продукція С має виготовлятися в кількості не менш як 9 одиниць.
Розв'язування. Математичну модель сформульованої задачі запишемо так:
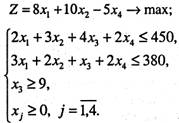
Застосовуючи для розв’язування поставленої задачі симплекс-метод, спочатку записуємо систему обмежень у канонічній формі, а далі — у векторній:
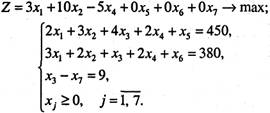
Зауважимо, що нерівність типу «>» у рівняння перетворюємо введенням у ліву частину обмеження додаткової змінної зі знаком «-».
Векторна форма запису:
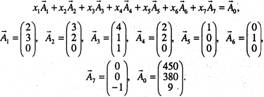
Серед записаних векторів є лише Два одиничні — ![]() та
та ![]() , а базис у тривимірному просторі має складатися з трьох одиничних векторів. Ще один одиничний вектор можна дістати, увівши в третє обмеження з коефіцієнтом +1 штучну змінну х8 якій відповідатиме одиничний вектор
, а базис у тривимірному просторі має складатися з трьох одиничних векторів. Ще один одиничний вектор можна дістати, увівши в третє обмеження з коефіцієнтом +1 штучну змінну х8 якій відповідатиме одиничний вектор
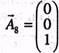
Тепер можемо розглянути розширену задачу лінійного програмування:
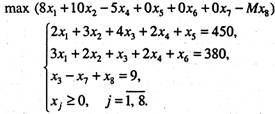
На відміну від додаткових змінних штучна змінна ![]() має в цільовій функції Z коефіцієнт +М (для задачі на min) або -М (для задачі на max), де М— досить велике додатне число.
має в цільовій функції Z коефіцієнт +М (для задачі на min) або -М (для задачі на max), де М— досить велике додатне число.
У розширеній задачі базисними змінними є x5, х6, х8, а решта змінних вільні. Початковий опорний план задачі:
![]()
Складемо першу симплексну таблицю задачі:
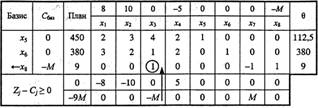
Розраховуючи оцінки першого опорного плану, дістаємо z0 = 0 - 9М, Z1 – С1 = -8, Z2 – С2 = -10, Z3 - С3 = 0 - М і т. д. Як бачимо, значення оцінок складаються з двох частин, одна з яких містить М, а інша — просто число. Тому для зручності розбиваємо оцінковий рядок на два. У перший оцінковий рядок записуємо просто число, а в другий — число з коефіцієнтом М.
Оцінки першого плану не задовольняють умову оптимальності, і тому він є неоптимальним. Згідно з алгоритмом, розглянутим у задачі 2.41, виконуємо перехід до наступного опорного плану задачі.
Подальше розв'язування задачі наведене у вигляді таблиці:
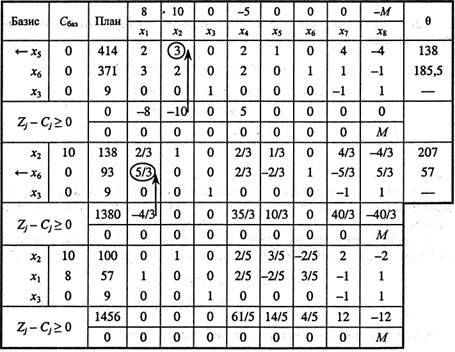
Оптимальним планом задачі є вектор
![]()
Отже, оптимальним є виробництво 57 одиниць продукції А, 100 одиниць продукції В і 9 одиниць продукції С. Тоді прибуток буде найбільшим і становитиме 1456 дол.
Висновок
Зміст математичного програмування складає теорія і методи розв’язання задач про знаходження екстремумів функції на множинах, які визначаються лінійними і нелінійними обмеженнями (рівностями і нерівностями).
Лінійне математичне програмування являє собою розв’язок задач: загальної, канонічної і стандартної форми.
Загальна форма задачі лінійного програмування не є досить простим і ефективним способом розв’язання її. Тому, як правило, задачу зводять до стандартної форми. В залежності від методів, які застосовуються, розрізняють дві стандартні форми: першу і другу.
При розв’язанні задач лінійного програмування майже завжди складають математичну модель. Математична модель стандартної задачі – це її спрощений образ, поданий у вигляді сукупності математичних нерівностей.
Література
1. Цегелик Г.Г. Лінійне програмування. – Львів, 1995.
2. Акулич. Математичне програмування в прикладах і задачах. – Москва, 1986.
3. Математичне програмування. Навч.-метод. Посібник для самостійного вивчення дисципліни / В.В. Вітлінський, С.І. Наконечний, Т.О. Терещенко. М-во освіти і науки України. КНЕУ. – К.: КНЕУ, 2001.
4. Математичне програмування [Текст] навч. посібник для студ. вищ. закладів, І.Ю. Іванченко. – К.: ЦУЛ, 2007.
5. Математическое программирование и моделирование экономических процессов: Учеб. для студ. лесотехн. вузов. – Санкт-Петербург, гос. лесотехн. акад. СПб: Изд-во ДНК, 2003.
6. Математичне програмування. Навч. посібник для студентів напрямів «Економіка і підприємство», «Менеджмент» / А.Ф. Барвінський, І.Я. Олексів, З.І. Крупка та ін.; М-во освіти і науки України. Нац. Ун-т «Львів. політехніка». – Л.: Інтелект-Захід, 2004.
7. Математичне програмування: Навч. посібник / С.І. Наконечний, С.С. Савіна; М-во освіти і науки України. КНЕУ. – К.: КНЕУ, 2003.
8. Гасс С. Линейное программирование (методы и приложения). Пер. с англ. Гольштейна Е.П. и Сушкевича М.И. Под ред. Юдина Д.Б. – М.: Физат гиз, 1961.
9. Математичне програмування: Навч. посібник / В.М.Дякон, Л.Є.Ковальов; за заг. ред. В.М. Міхайленка. – К.: Вид-во Європ. ун-ту, 2007.
10. Мазаракі А.А., Толбатов Ю.А. Математичне програмування. Excel: Навч. посіб. для студ. екон. спеціал. вузів. – К.: Четверта хвиля, 1998.
Похожие работы
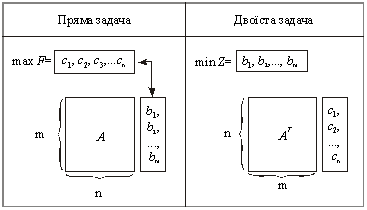
... виокремлюють певні підкласи. Наприклад, ігри двох осіб із нульовою сумою. Наведену класифікацію використано для структурування курсу «Математичне програмування». 2. Економічна інтерпретація прямої та двоїстої задач лінійного програмування Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари таких задач розглянемо ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
ача має назву задачі безумовного програмування. У якості прикладів економічних проблем, які доцільно розв’язувати. використовуючи методи та моделі математичного програмування, розглянемо такі: Приклад 1. Задача про планування випуску продукції малого підприємства. Планується виробляти жіночі та чоловічі костюми. На жіночій костюм потрібно 1 м. шерсті, 2 м. шовку та 1 людино-тиждень працевитрат. ...
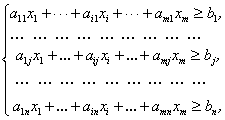
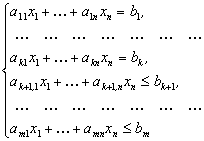

0 комментариев