Навигация
Зависимость доверительных интервалов коэффициентов уравнения от заданного уровня надежности
5.1.2 Зависимость доверительных интервалов коэффициентов уравнения от заданного уровня надежности
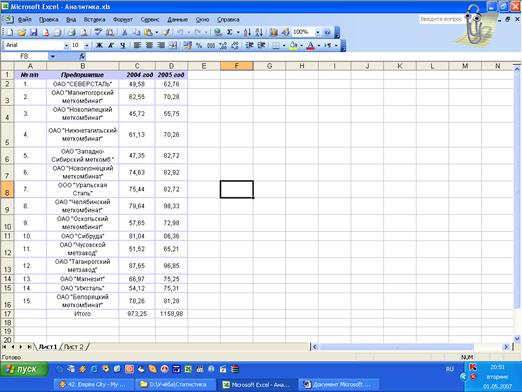
Доверительные интервалы коэффициентов а0, а1 построенного уравнения регрессии при уровнях надежности Р=0,95 и Р=0,683 представлены в табл.2.7, на основе которой формируется табл.2.9.
Таблица 2.9
Границы доверительных интервалов коэффициентов уравнения
| Коэффициенты | Границы доверительных интервалов | |||
| Для уровня надежности Р=0,95 | Для уровня надежности Р=0,683 | |||
| нижняя | верхняя | нижняя | верхняя | |
| а0 | -1548,8999 | 157,7979 | -1119,9924 | -271,1096 |
| а1 | 0,9012 | 1,2776 | 0,9957 | 1,1830 |
Вывод:
В генеральной совокупности предприятий значение коэффициента а0 следует ожидать с надежностью Р=0,95 в пределах -1548,8999 а0 157,7979, значение коэффициента а1 в пределах 0,9012 а1 1,2776. Уменьшение уровня надежности ведет к расширению (сужению) доверительных интервалов коэффициентов уравнения.
Определение практической пригодности построенной регрессионной модели.
Практическую пригодность построенной модели ![]() можно охарактеризовать по величине линейного коэффициента корреляции r:
можно охарактеризовать по величине линейного коэффициента корреляции r:
· близость ![]() к единице свидетельствует о хорошей аппроксимации исходных (фактических) данных с помощью построенной линейной функции связи
к единице свидетельствует о хорошей аппроксимации исходных (фактических) данных с помощью построенной линейной функции связи ![]() ;
;
· близость ![]() к нулю означает, что связь между фактическими данными Х и Y нельзя аппроксимировать как построенной, так и любой другой линейной моделью, и, следовательно, для моделирования связи следует использовать какую-либо подходящую нелинейную модель.
к нулю означает, что связь между фактическими данными Х и Y нельзя аппроксимировать как построенной, так и любой другой линейной моделью, и, следовательно, для моделирования связи следует использовать какую-либо подходящую нелинейную модель.
Пригодность построенной регрессионной модели для практического использования можно оценить и по величине индекса детерминации R2, показывающего, какая часть общей вариации признака Y объясняется в построенной модели вариацией фактора X.
В основе такой оценки лежит равенство R = r(имеющее место для линейных моделей связи), а также шкала Чэддока, устанавливающая качественную характеристику тесноты связи в зависимости от величины r.
Согласно шкале Чэддока высокая степень тесноты связи признаков достигается лишь при ![]() >0,7, т.е. при
>0,7, т.е. при ![]() >0,7. Для индекса детерминации R2 это означает выполнение неравенства R2 >0,5.
>0,7. Для индекса детерминации R2 это означает выполнение неравенства R2 >0,5.
При недостаточно тесной связи признаков X, Y (слабой, умеренной, заметной) имеет место неравенство ![]()
![]() 0,7, а следовательно, и неравенство
0,7, а следовательно, и неравенство ![]() .
.
С учетом вышесказанного, практическая пригодность построенной модели связи ![]() оценивается по величине R2 следующим образом:
оценивается по величине R2 следующим образом:
· неравенство R2 >0,5 позволяет считать, что построенная модель пригодна для практического применения, т.к. в ней достигается высокая степень тесноты связи признаков X и Y, при которой более 50% вариации признака Y объясняется влиянием фактора Х;
· неравенство ![]() означает, что построенная модель связи практического значения не имеет ввиду недостаточной тесноты связи между признаками X и Y, при которойменее 50% вариации признака Y объясняется влиянием фактора Х, и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели) факторы.
означает, что построенная модель связи практического значения не имеет ввиду недостаточной тесноты связи между признаками X и Y, при которойменее 50% вариации признака Y объясняется влиянием фактора Х, и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели) факторы.
Значение индекса детерминации R2 приводится в табл.2.5 в ячейке В79 (термин "R - квадрат").
Вывод:
Значение линейного коэффициента корреляции r и значение индекса детерминации R2 согласно табл. 2.5 равны: r =0,9132, R2 =0,8339. Поскольку и , то построенная линейная регрессионная модель связи пригодна (не пригодна) для практического использования.
Общая оценка адекватности регрессионной модели по F-критерию Фишера
Адекватность построенной регрессионной модели фактическим данным (xi, yi) устанавливается по критерию Р.Фишера, оценивающему статистическую значимость (неслучайность) индекса детерминации R2.
Рассчитанная для уравнения регрессии оценка значимости R2 приведена в табл.2.6 в ячейке F86 (термин "Значимость F"). Если она меньше заданного уровня значимости α=0,05, то величина R2 признается неслучайной и, следовательно, построенное уравнение регрессии ![]() может быть использовано как модель связи между признаками Х и Y для генеральной совокупности предприятий отрасли.
может быть использовано как модель связи между признаками Х и Y для генеральной совокупности предприятий отрасли.
Вывод:
Рассчитанный уровень значимости αр индекса детерминации R2 есть αр=0. Так как он меньше(больше) заданного уровня значимости α=0,05, то значение R2 признается типичным (случайным) и модель связи между признаками Х и Y -695,5510+1,0894х применима (неприменима) для генеральной совокупности предприятий отрасли в целом.
Оценка погрешности регрессионной модели
Погрешность регрессионной модели можно оценить по величине стандартной ошибки ![]() построенного линейного уравнения регрессии
построенного линейного уравнения регрессии ![]() . Величина ошибки
. Величина ошибки ![]() оценивается как среднее квадратическое отклонение по совокупности отклонений
оценивается как среднее квадратическое отклонение по совокупности отклонений ![]() исходных (фактических) значений yi признака Y от его теоретических значений
исходных (фактических) значений yi признака Y от его теоретических значений ![]() , рассчитанных по построенной модели.
, рассчитанных по построенной модели.
Погрешность регрессионной модели выражается в процентах и рассчитывается как величина ![]() .100.
.100.
В адекватных моделях погрешность не должна превышать 12%-15%.
Значение ![]() приводится в выходной таблице "Регрессионная статистика" (табл.2.5) в ячейке В81 (термин "Стандартная ошибка"), значение
приводится в выходной таблице "Регрессионная статистика" (табл.2.5) в ячейке В81 (термин "Стандартная ошибка"), значение ![]() – в таблице
описательных статистик (ЛР-1, Лист 1, табл.3, столбец 2).
– в таблице
описательных статистик (ЛР-1, Лист 1, табл.3, столбец 2).
Вывод:
Погрешность линейной регрессионной модели составляет .100= .100=9,1749%, что подтверждает (не подтверждает) адекватность построенной модели -695,5510+1,0894х.
Задача 6
Дать экономическую интерпретацию:
1) коэффициента регрессии а1;
3) остаточных величин ![]() i.
i.
2) коэффициента эластичности КЭ;
6.1 Экономическая интерпретация коэффициента регрессии а1
В случае линейного уравнения регрессии ![]() =a0+a1x величина коэффициента регрессии a1 показывает, на сколько в среднем (в абсолютном выражении) изменяется значение результативного признака Y при изменении фактора Х на единицу его измерения. Знак при a1 показывает направление этого изменения.
=a0+a1x величина коэффициента регрессии a1 показывает, на сколько в среднем (в абсолютном выражении) изменяется значение результативного признака Y при изменении фактора Х на единицу его измерения. Знак при a1 показывает направление этого изменения.
Вывод:
Коэффициент регрессии а1 =1,0894 показывает, что при увеличении факторного признака Среднегодовая стоимость основных производственных фондов на 1 млн руб. значение результативного признака Выпуск продукции увеличивается (уменьшается) в среднем на 1,0894 млн руб.
Похожие работы
... в отчетном периоде по сравнению с базисным увеличились на 4,68% 3. Аналитическая часть В этой части работы изложены результаты проведенного статистического исследования изменения уровня затрат на рубль товарной продукции организаций. Изучение проводилось средствами пакета программ MS Excel. 3.1 Постановка задачи Произвести исследование изменения уровня затрат на рубль товарной ...
... для малых предприятий всех организационно-правовых форм и форм собственности и годовая форма, содержащая показатели производственной деятельности этих предприятий. Общее руководство статистическим наблюдением за деятельностью коммерческих банков возложено на Банк России, который совместно с органами государственной статистики разрабатывает формы статистической отчетности и инструкции по их ...
... цену приобретения акций: Решение Воспользуемся для определения средней цены формулой (7): руб. В практике реальных расчетов взвешенные средние гармонические используются чаще. 4. Понятие, виды и показатели вариации Рассматривая зарегистрированные при статистическом наблюдении величины того или иного признака у отдельных единиц совокупности, обнаруживаем, что они различаются между ...
... я хотела бы посвятить именно приемному отделению ТК «Жуковка». Я считаю, что будет вполне целесообразно разработать и внедрить на данном предприятии автоматизированную информационную систему планирования сбыта, что в свою очередь ускорит и существенно облегчит работу приемного отделения ТК «Жуковка». План-схема приемного отделения и структура работы службы приема и размещения ТК «Жуковка» ...





0 комментариев