Навигация
Показатели, рассчитываемые на основе рядов динамики
1.2 Показатели, рассчитываемые на основе рядов динамики
Уровни временного ряда могут изменяться в самых разных направлениях: они могут возрастать или убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:
Абсолютный прирост (∆у)
Темп роста (Тр)
Коэффициент роста (Кр)
Темп прироста (снижения) (Тпр)
Абсолютное значение на 1% прироста (А)
Абсолютный прирост (абсолютное изменение) уровней ряда рассчитывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.
В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:
∆у цепной = уi – yi – 1;
∆базисный = yi – y0
Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным.
Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.
Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения (таб. 3):[3]
Таблица 3
| года | Произведено продукции, тыс. шт. | Абсолютные приросты, тыс. шт. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. шт. | |||
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| 1995 | 20 | - | - | - | 100 | - | - | - |
| 1996 | 25 | 5 | 5 | 125 | 125 | 25 | 25 | 0,2 |
| 1997 | 35 | 10 | 15 | 140 | 175 | 40 | 75 | 0,25 |
| 1998 | 40 | 5 | 20 | 114,3 | 200 | 14,3 | 100 | 0,35 |
| 1999 | 50 | 10 | 30 | 125 | 250 | 25 | 150 | 0,40 |
| Итого | 170 | 30 | - | - | - | - | - | - |
В данном примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым – 5 тыс. шт., но интенсивность роста объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25%, а в 1998 г. по сравнению с предыдущим годом – лишь 14,3%. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. – прирост составил по сравнению с предыдущим годом 40%, а в 1999 г. – 25%.
Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:
Тр цепной ![]() ;
;
Tp базисный ![]()
Если база сравнения по периодам меняется, то найденные темпы поста называются цепными. Если же база сравнения по периодам неизменна (у0), то темпы роста называются базисными.
Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:
Кp цепной ![]()
Кз базисный ![]()
В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % (темп роста) и в разах (коэффициент роста).
Так, по данным таблицы 3 можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140%, или в 1,4 раза превысил уровень предыдущего года.
Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста (снижения) за весь интервал времени между текущим и базисным уровнями. Так, по данным таблицы 3 базисный темп роста за весь период с 1996 по 1999 г. составил 250% (1995 г. взят за базу сравнения).
Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель).
∆Тр цепной = ![]()
∆Тр базисный = ![]()
По данным таблицы 3 темп прироста для 1999 г. составит: цепной – 25% (![]() ) и базисный – 150% (
) и базисный – 150% (![]() ), т. е. в 1999 г. объем продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь рассматриваемый период прирост составил 150%.
), т. е. в 1999 г. объем продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь рассматриваемый период прирост составил 150%.
Между цепными и базисными показателями изменения уровня ряда существует следующая взаимосвязь:
А) сумма цепных абсолютных приростов равно базисному приросту (см. в таблице 3, где в итоговой строке накопленный прирост за 1996 – 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным ростом для 1999 г.);
Б) произведение цепных коэффициентов роста равно базисному.
В) произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентом роста. Так по данным таблице 3 имеем:
1,25 • 1,40 • 1,43 • 1,25 = 2,5, или 250% - базисный темп роста;
200/175 = 1,143, или 114,3% - цепной коэффициент роста для 1998 г.
Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;
Г) Темп прироста связан с темпом роста: ∆Тр – Тр – 100 (см. таблицу 3, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один инз них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста.
Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.
Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим (таб. 4).
Таблица 4
Изменение цен (в % к предыдущему месяцу)
| Месяц | Январь | Февраль | Март |
| Изменение цен | 3,7 | 1,7 | 1,8 |
В целом за I квартал прирост цен составит:
(1,037 ×1,017×1,018) • 100 = 7,4%.
То есть в марте 2001 года по сравнению с декабрем 2000 года цены выросли на 7,4%.
Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени:
А = ![]() или
или
А = 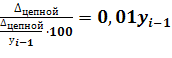 .
.
Иными словами, абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. таблице 3, последнюю графу). В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.
Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как ∆″ = ∆i - ∆i – 1, то есть по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По таблице 3 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда ∆″ = 10 – 5 = 5 тыс. шт.
Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:
∆% = Трi – Трi – 1
Или
∆% = ∆Трi - ∆Npi – 1.
Полученная величина выражается в процентных пунктах (п.п.). По данным таблицы 3, относительное ускорение имело место лишь в 1997 г. – 15 процентных пунктов по сравнению с предыдущим годом.
Относительное ускорение может быть измерено и с помощью коэффициента опережения.
Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:
Копережения = ![]() .
.
В нашем примере коэффициент опережения для 1997 года составил 140/125 = 1,12, что означает, что в 1997 году темп роста был в 1,12 раза больше, чем в 1996 году.
Коэффициент опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменений уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому (таб. 5).
Таблица 5
Динамика доходов предприятия за 1-е полугодие 2001 г.
| Месяцы | Прибыль от реализации продукции | Прибыль от продажи прочих активов | Доходы по акциям |
| Декабрь 2000 г. | 205 | 30 | 21 |
| 2001 г.: Январь | 220 | 32 | 27 |
| Февраль | 226 | 40 | 32 |
| Март | 252 | 48 | 38 |
| Апрель | 280 | 60 | 54 |
| Май | 310 | 100 | 66 |
| Июнь | 356 | 120 | 88 |
Во всех рядах заметна тенденция к росту из месяца в месяц отдельных видов доходов. Однако сделать вывод об интенсивности роста отдельных видов доходов только по данным таблицы 5 затруднительно. Для наглядности приведем к одному основанию, приняв для каждого из них за базу сравнения декабрь 2000 г. (таб. 6).
Таблица 6
Динамика доходов предприятия за 1-е полугодие 2001 г.
| Месяцы | Прибыль от реализации продукции | Прибыль от продажи прочих активов | Доходы по акциям |
| Декабрь 2000 г. | 100 | 100 | 100 |
| 2001 г.: Январь | 107,3 | 106,7 | 128,6 |
| Февраль | 110,2 | 133,3 | 152,4 |
| Март | 122,9 | 160,0 | 181,0 |
| Апрель | 136,6 | 200,0 | 257,1 |
| Май | 151,2 | 333,3 | 314,3 |
| Июнь | 173,7 | 400,0 | 419,0 |
Как видим, наиболее интенсивно на предприятии росли доходы по акциям, а также прибыль от продажи прочих активов. Коэффициент опережения их роста за 1-е полугодие по сравнению с ростом прибыли от реализации продукции составили: 2,3 – для прибыли от продажи прочих активов и 2,4 – для доходов по акциям.
При анализе, произведенном на основе вышерассмотренных данных, приводятся средние показатели. То есть:
Средний уровень интервального ряда динамики
![]() , где n – число периодов.
, где n – число периодов.
Средний абсолютный прирост
![]() , где n – число периодов или
, где n – число периодов или
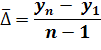
Средний коэффициент роста
![]()
или
![]() =
= ![]()
Средний темп роста
![]() =
= ![]()
Средний темп прироста
![]() - 1)
- 1)![]()
или
![]() - 100
- 100
Средняя величина абсолютного значения на 1 единицу % прироста
![]() =
= ![]()
Глава II. Статистический анализ по рядам динамики на примере предприятия «Салон красоты Goddess
0 комментариев