Навигация
1. f(x)=x
f(x)=x2
f(x)= x3
f(x)= x4
на отрезке [0, 1] с шагом ![]() ,
, ![]() ,
, ![]()
2. f(x)=![]()
f(x)=![]()
f(x)=![]()
3. Выполнить вариант индивидуального задания (таблица 2)
Таблица 2 Индивидуальные варианты задания
| № | Функция f(x) | Отрезок интегрирования [a,b] |
| 1 |
| [1;3] |
| 2 |
| [1;3] |
| 3 |
| [0;2] |
| 4 |
| [2;4] |
| 5 |
| [1;3] |
| 6 |
| [0;2] |
| 7 |
| [0;2] |
| 8 |
| [1;3] |
| 9 |
| [0;2] |
| 10 |
| [0;2] |
| 11 |
| [1;3] |
| 12 |
| [1;3] |
| 13 |
| [0;2] |
| 14 |
| [2;4] |
| 15 |
| [1;3] |
| 16 |
| [0;2] |
| 17 |
| [0;2] |
| 18 |
| [1;3] |
| 19 |
| [0;2] |
| 20 |
| [0;2] |
| 21 |
| [1;3] |
| 22 |
| [1;3] |
| 23 |
| [0;2] |
| 24 |
| [2;4] |
| 25 |
| [1;3] |
| 26 |
| [0;2] |
| 27 |
| [0;2] |
| 28 |
| [1;3] |
| 29 |
| [0;2] |
| 30 |
| [0;2] |
2) Провести сравнительный анализ методов.
Вычисление определенного интеграла: Методические указания к лабораторной работе по дисциплине «Вычислительная математика» / сост. И.А.Селиванова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 14 с.
Указания предназначены для студентов всех форм обучения специальности 230101 – «Вычислительные машины, комплексы, системы и сети» и бакалавров направления 230100 – «Информатика и вычислительная техника». Составитель Селиванова Ирина Анатольевна
Похожие работы
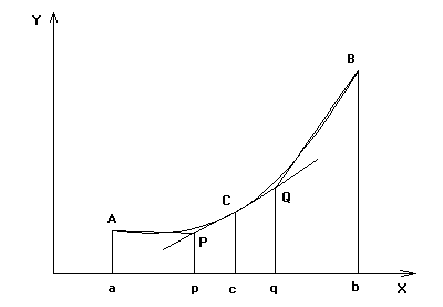
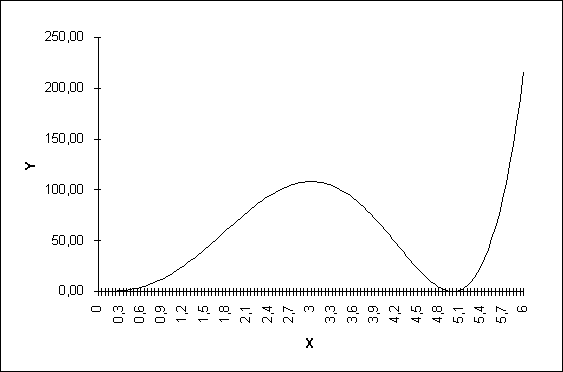
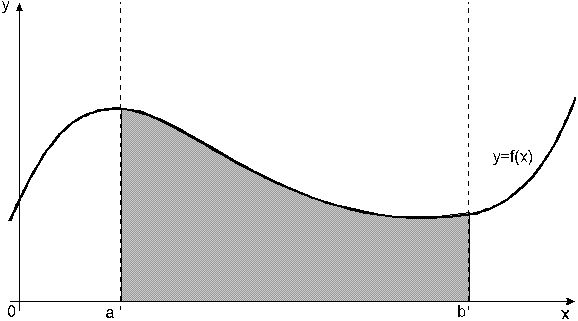
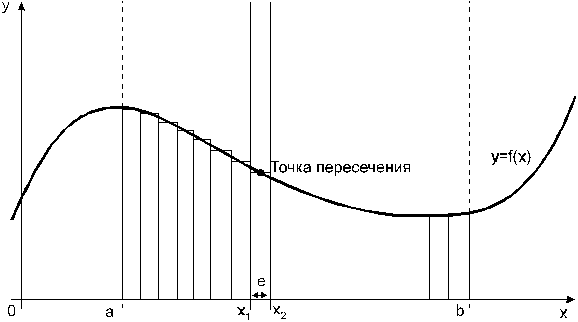
ределенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). Рис. 1. Криволинейная трапеция. Рис. 2. Метод трапеций. Рис. 3. Метод средних прямоугольников. По методам ...
... , т. е. знакопостоянна. рис. 2 Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью формулы Симпсона. Программа состоит из трех функций main, f и integral. Функция main вызывает функцию integral для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение ...
... процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
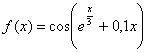
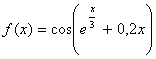
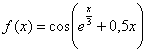



0 комментариев