МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА ИНФОРМАТИКИ
Курсовая работа
по дисциплине «Численные методы»
на тему:
«Вычисление характеристических многочленов, собственных значений и собственных векторов»
Сумы, 2005
Содержание
СОДЕРЖАНИЕ
ТЕОРЕТИЧЕСКИЕ ДАННЫЕ
ВВЕДЕНИЕ
МЕТОД ДАНИЛЕВСКОГО
УКАЗАНИЯ ПО ПРИМЕНЕНИЮ ПРОГРАММЫ
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
АНАЛИЗ ПРОГРАММЫ
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Теоретические данные
ВведениеБольшое количество задач с механики, физики и техники требует нахождение собственных значений и собственных векторов матриц, т.е. таких значений λ, для которых существует нетривиальное решение однородной системы линейных алгебраических уравнений ![]() . Тут А-действительная квадратичная матрица порядка n с элементами ajk, а
. Тут А-действительная квадратичная матрица порядка n с элементами ajk, а ![]() --вектор с компонентами x1, x2,…, xn Каждому собственному значению λi соответствует хотя бы одно нетривиальное решение. Если даже матрица А действительная, ей собственные числа (все или некоторые) и собственные векторы могут быть недействительными. Собственные числа являются корнями уравнения
--вектор с компонентами x1, x2,…, xn Каждому собственному значению λi соответствует хотя бы одно нетривиальное решение. Если даже матрица А действительная, ей собственные числа (все или некоторые) и собственные векторы могут быть недействительными. Собственные числа являются корнями уравнения ![]() , где Е - единичная матрица порядка n
, где Е - единичная матрица порядка n
или 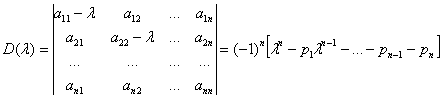
Данное уравнение называется характеристическим уравнением матрицы А. Собственным векторам ![]() , которым соответствует собственному значению λi, называют ненулевое решение однородной системы уравнений
, которым соответствует собственному значению λi, называют ненулевое решение однородной системы уравнений ![]() . Таким образом, задача нахождения собственных чисел и собственных векторов сводится к нахождению коэффициентов характеристического уравнения, нахождению его корней и нахождению нетривиального решения системы.
. Таким образом, задача нахождения собственных чисел и собственных векторов сводится к нахождению коэффициентов характеристического уравнения, нахождению его корней и нахождению нетривиального решения системы.
Метод Данилевского
Простой и изысканный метод нахождения характеристического многочлена предложил А.М.Данилевский. Рассмотрим идею метода. Рассмотрим матрицу A

Для которой находится характеристический многочлен, при помощи подобных преобразований преобразуется к матрице
 ,
,
которая имеет нормальную форму Фробениуса, то есть матрица имеет в явном виде в последнем столбце искомые коэффициенты характеристического уравнения. Т. к. подобные матрицы имеют один и тот же характеристический многочлен, а
![]() , то и
, то и ![]() .
.
Поэтому для обоснования метода достаточно показать, каким образом из матрицы A строится матрица P.
Подобные преобразования матрицы A к матрице P происходят последовательно. На первом шаге матрица А преобразовывается к подобной до неё матрице А(1), в которой предпоследний столбец имеет необходимый вид. На втором шаге матрица А(1) преобразовывается на подобную к ней матрицу А(2), в которой уже два предпоследних столбца имеют необходимый вид, и т.д.
На первом шаге матрица А умножается справа на матрицу

и слева на матрицу ей обратную
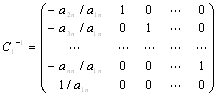
Первый шаг даёт
 ,
,
где 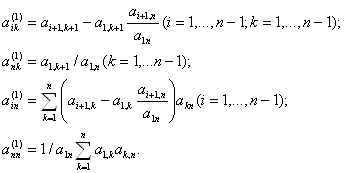
На втором шаге матрица А(1) умножается справа на матрицу

и слева на обратную к ней матрицу
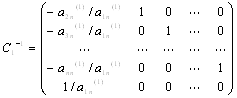
Очевидно, что элементы матрицы
![]() .
. 
Это означает, что два предпоследних столбца матрицы А(2) имеют необходимый вид. Продолжая этот процесс, после n-1 шагов придем к матрице
 ,
,
которая имеет форму Фробениуса и подобная к входной матрице А. При этом на каждом шаге элементы матрицы А(j) находятся по элементам матрицы А(j-1) также, как мы находили элементы матрицы А(2) по элементам А(1). При этом предпологается, что все элементы ![]() отличные от нуля. Если на j-ом шаге окажется, что
отличные от нуля. Если на j-ом шаге окажется, что ![]() , то продолжать процесс в таком виде не будет возможно. При этом могут возникнуть два случая:
, то продолжать процесс в таком виде не будет возможно. При этом могут возникнуть два случая:
1. Среди элементов ![]() есть хотя бы один, отличный от нуля, например
есть хотя бы один, отличный от нуля, например ![]() . Для продолжения процесса поменяем в А(j) местами первый и
. Для продолжения процесса поменяем в А(j) местами первый и ![]() -й строчки и одновременно 1-й и
-й строчки и одновременно 1-й и ![]() -й столбцы. Такое преобразование матрицы А(j) будет подобным. После того, как получим матрицу
-й столбцы. Такое преобразование матрицы А(j) будет подобным. После того, как получим матрицу ![]() , процесс можно продолжать, т.к. столбцы матрицы А(j),приведённые к необходимому виду не будут испорчены.
, процесс можно продолжать, т.к. столбцы матрицы А(j),приведённые к необходимому виду не будут испорчены.
2. Все элементы ![]() равны нулю. Тогда матрица А(j) имеет вид
равны нулю. Тогда матрица А(j) имеет вид 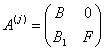 , где F- квадратичная матрица порядка j, которая имеет нормальный вид Фробениуса; В—квадратная матрица порядка n-j, но
, где F- квадратичная матрица порядка j, которая имеет нормальный вид Фробениуса; В—квадратная матрица порядка n-j, но ![]() , то есть характеристический многочлен матрицы F является делителем характеристического многочлена матрицы А. Для нахождения характеристического многочлена матрицы А необходимо еще найти характеристический многочлен матрицы В, для которой используем этот же метод.
, то есть характеристический многочлен матрицы F является делителем характеристического многочлена матрицы А. Для нахождения характеристического многочлена матрицы А необходимо еще найти характеристический многочлен матрицы В, для которой используем этот же метод.
Подсчитано, что количество операций умножения и деления, необходимых для получения характеристического многочлена матрицы порядка n составляет n(n-1)(2n+3)/2.
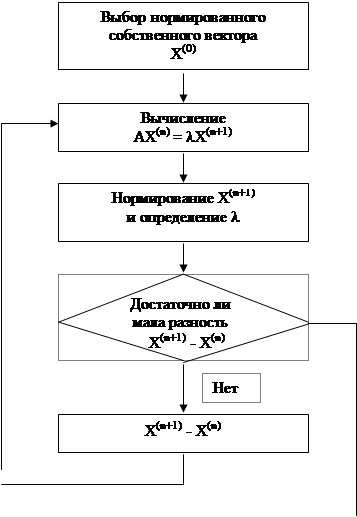
На данном этапе работы мы получили характеристический полином, корнями которого будут собственные числа матрицы А. Процедура нахождения корней полинома n-ой степени не проста. Поэтому воспользуемся пакетом MathCAD Professional для реализации данной задачи. Для поиска корней обычного полинома р(х) степени n в Mathcad включена очень удобная функция polyroots(V). Она возвращает вектор всех корней многочлена степени n, коэффициенты которого находятся в векторе V, имеющим длину равную n+1. Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Таким образом мы имеем собственные числа, при помощи которых мы найдём собственные векторы нашей матрицы А. Для нахождения собственных векторов воспользуемся функцией eigenvec(A,vi), где А-исходная матрица, vi-собственное число, для которого мы ищем собственный вектор. Данная функция возвращает собственный вектор дня vi.
Указания по применению программыДанная курсовая работа выполнена на языке программирования Pascal. В курсовую работу входит файл danil.exe. Danil.exe предназначен для нахождения характеристического полинома методом Данилевского. Входными параметрами является размерность матрицы и сама матрица, а выходным — характеристический полином.
Программная реализацияПрограммный код программы danil.exe
uses wincrt;
label 1;
type mas=array[1..10,1..10]of real;
var A,M,M1,S:mas;
z,max:real;
f,jj,tt,ww,v,h,b,y,i,j,w,k,e,l,q,x,u:byte;
p,o:array[1..10]of real;
t:array [1..10]of boolean;
procedure Umnogenie(b,c:mas; n:byte; var v:mas);
var i,j,k:byte;
begin
for i:=1 to n do
for j:=1 to n do
begin
v[i,j]:=0;
for k:=1 to n do
v[i,j]:=b[i,k]*c[k,j]+v[i,j];
end;
end;
procedure dan(n:byte; var a:mas);
label 1,2;
var y:byte;
begin
For y:=1 to n-1 do
begin
if a[1,n]=0 then
begin
if y>1 then begin
max:=abs(a[1,n]);
w:=1;
for i:=1 to n-y do
if abs(a[i,n])>max then begin max:=abs(a[i,j]); w:=i; end;
if max=0 then
begin
for l:=n downto n-y+1 do
begin
p[f]:=a[l,n];
t[f]:=false;
f:=f-1;
end;
t[f+1]:=true;
x:=x+1;
u:=n-y;
if y=n-1 then begin o[q]:=a[1,1]; q:=q+1; end else dan(u,a);
goto 2;
end;
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[w,j];
a[w,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,w];
a[k,w]:=z;
end;
goto 1;
end
else
begin
max:=abs(a[1,2]);
w:=1;e:=2;
for i:=1 to n-1 do
if abs(a[i,n])>max then begin max:=abs(a[i,j]); w:=i; e:=n; end;
for j:=2 to n do
if abs(a[1,j])>max then begin max:=abs(a[i,j]); w:=1; e:=j; end;
if abs(a[n,1])>max then begin max:=abs(a[n,1]); w:=n; e:=1; end;
if max=0 then
begin
o[q]:=a[n,n];
q:=q+1;
u:=n-1;
if n=2 then begin o[q]:=a[1,1]; q:=q+1; o[q]:=a[n,n]; q:=q+1; end else dan(u,a);
goto 2;
end;
if (w>1) and (e=n) then
begin
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[w,j];
a[w,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,w];
a[k,w]:=z;
end;
goto 1;
end;
if (w=n) and (e=1) then
begin
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[n,j];
a[n,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,n];
a[k,n]:=z;
end;
goto 1;
end;
if w=1 then
begin
for j:=1 to n do
begin
z:=a[n,j];
a[n,j]:=a[e,j];
a[e,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,n];
a[k,n]:=a[k,e];
a[k,e]:=z;
end;
goto 1;
end;
end;
end;
1:
for i:=1 to n do
for j:=1 to n do
if i<>(j+1) then M[i,j]:=0
else M[i,j]:=1;
for i:=1 to n do
for j:=1 to n do
if (i+1)<>j then M1[i,j]:=0
else M1[i,j]:=1;
for i:=1 to n do
if i<>n then begin M[i,n]:=a[i,n]; M1[i,1]:=-a[i+1,n]/a[1,n]; end
else begin M[i,n]:=a[i,n]; M1[i,1]:=1/a[1,n]; end;
Umnogenie(M1,A,n,S);
Umnogenie(S,M,n,A);
if y=n-1 then
begin
for l:=n downto 1 do
begin
p[f]:=a[l,n];
t[f]:=false;
f:=f-1;
end;
t[f+1]:=true;
x:=x+1;
end;
end;
2:
end;
begin
writeln('Vvedite razmernost` matrici A');
readln(ww);
f:=ww;
for i:=1 to ww do
begin
for j:=1 to ww do
begin
write('a[',i,j,']=');
Readln(A[i,j]);
end;
end;
q:=1;
x:=0;
dan(ww,a);
for i:=1 to q-1 do
writeln('Koren` har-ogo ur-iya=',o[i]:2:2);
writeln;
i:=ww+1;
if (x=1)or(x>1) then
begin
for v:=1 to x do
begin
tt:=0;
repeat
tt:=tt+1;
i:=i-1;
until t[i]<>false;
write('l^',tt,' + ');
for jj:=ww downto i do
begin
tt:=tt-1;
write(-p[jj]:2:2,'*l^',tt,' + ');
end;
ww:=i-1;
writeln;
end;
end;
end.
Получение формы Жордано: form.exe
uses wincrt;
label 1;
type mas=array[1..10,1..10]of real;
var A,M,M1,S,R,R1,A1:mas;
z,max:real;
f,jj,tt,ww,v,h,b,y,i,j,w,k,e,l,q,x,u,n1:byte;
p,o:array[1..10]of real;
t:array [1..10]of boolean;
procedure Umnogenie(b,c:mas; n:byte; var v:mas);
var i,j,k:byte;
begin
for i:=1 to n do
for j:=1 to n do
begin
v[i,j]:=0;
for k:=1 to n do
v[i,j]:=b[i,k]*c[k,j]+v[i,j];
end;
end;
procedure dan(n:byte; var a:mas);
label 1,2;
var y:byte;
begin
For y:=1 to n-1 do
begin
if a[1,n]=0 then
begin
if y>1 then begin
max:=abs(a[1,n]);
w:=1;
for i:=1 to n-y do
if abs(a[i,n])>max then begin max:=abs(a[i,j]); w:=i; end;
if max=0 then
begin
for l:=n downto n-y+1 do
begin
p[f]:=a[l,n];
t[f]:=false;
f:=f-1;
end;
t[f+1]:=true;
x:=x+1;
u:=n-y;
if y=n-1 then begin o[q]:=a[1,1]; q:=q+1; end else dan(u,a);
goto 2;
end;
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[w,j];
a[w,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,w];
a[k,w]:=z;
end;
goto 1;
end
else
begin
max:=abs(a[1,2]);
w:=1;e:=2;
for i:=1 to n-1 do
if abs(a[i,n])>max then begin max:=abs(a[i,j]); w:=i; e:=n; end;
for j:=2 to n do
if abs(a[1,j])>max then begin max:=abs(a[i,j]); w:=1; e:=j; end;
if abs(a[n,1])>max then begin max:=abs(a[n,1]); w:=n; e:=1; end;
if max=0 then
begin
o[q]:=a[n,n];
q:=q+1;
u:=n-1;
if n=2 then begin o[q]:=a[1,1]; q:=q+1; o[q]:=a[n,n]; q:=q+1; end else dan(u,a);
goto 2;
end;
if (w>1) and (e=n) then
begin
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[w,j];
a[w,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,w];
a[k,w]:=z;
end;
goto 1;
end;
if (w=n) and (e=1) then
begin
for j:=1 to n do
begin
z:=a[1,j];
a[1,j]:=a[n,j];
a[n,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,1];
a[k,1]:=a[k,n];
a[k,n]:=z;
end;
goto 1;
end;
if w=1 then
begin
for j:=1 to n do
begin
z:=a[n,j];
a[n,j]:=a[e,j];
a[e,j]:=z;
end;
for k:=1 to n do
begin
z:=a[k,n];
a[k,n]:=a[k,e];
a[k,e]:=z;
end;
goto 1;
end;
end;
end;
1:
for i:=1 to n do
for j:=1 to n do
if i<>(j+1) then M[i,j]:=0
else M[i,j]:=1;
for i:=1 to n do
for j:=1 to n do
if (i+1)<>j then M1[i,j]:=0
else M1[i,j]:=1;
for i:=1 to n do
if i<>n then begin M[i,n]:=a[i,n]; M1[i,1]:=-a[i+1,n]/a[1,n]; end
else begin M[i,n]:=a[i,n]; M1[i,1]:=1/a[1,n]; end;
Umnogenie(M1,A,n,S);
Umnogenie(S,M,n,A);
if y=n-1 then
begin
for l:=n downto 1 do
begin
p[f]:=a[l,n];
t[f]:=false;
f:=f-1;
end;
t[f+1]:=true;
x:=x+1;
end;
end;
2:
end;
procedure ObrMatr(A:mas;Var AO:mas; n:byte);
const e=0.00001;
var i,j:integer;
a0:mas;
procedure MultString(var A,AO:mas;i1:integer;r:real);
var j:integer;
begin
for j:=1 to n do
begin
A[i1,j]:=A[i1,j]*r;
AO[i1,j]:=AO[i1,j]*r;
end;
end;
procedure AddStrings(var A,AO:mas;i1,i2:integer;r:real);
{Процедура прибавляет к i1 строке матрицы a i2-ю умноженную на r}
var j:integer;
begin
for j:=1 to n do
begin
A[i1,j]:=A[i1,j]+r*A[i2,j];
AO[i1,j]:=AO[i1,j]+r*AO[i2,j];
end;
end;
function Sign(r:real):shortint;
begin
if (r>=0) then sign:=1
else sign:=-1;
end;
begin {начало основной процедуры}
for i:=1 to n do
for j:=1 to n do
a0[i,j]:=A[i,j];
for i:=1 to n do
begin {К i-той строке прибавляем (или вычитаем)
j-тую строку взятую со знаком i-того
элемента j-той строки. Таким образом,
на месте элемента a[i,i] возникает сумма
модулей элементов i-того столбца (ниже i-той строки)
взятая со знаком бывшего элемента a[i,i],
равенство нулю которой говорит о несуществовании
обратной матрицы }
for j:=i+1 to n do
AddStrings(A,AO,i,j,sign(A[i,i])*sign(A[j,i])); { Прямой ход }
if (abs(A[i,i])>e) then
begin
MultString(a,AO,i,1/A[i,i]);
for j:=i+1 to n do
AddStrings(a,AO,j,i,-A[j,i]);
end
else begin writeln('Обратной матрицы не существует.');
halt;
end
end;{Обратный ход:}
if (A[n,n]>e) then begin
for i:=n downto 1 do
for j:=1 to i-1 do
begin
AddStrings(A,AO,j,i,-A[j,i]);
end; end
else writeln('Обратной матрицы не существует.');
end;
procedure EdMatr(Var E:mas; n:byte);
var i,j:byte;
begin
for i:=1 to n do
for j:=1 to n do
if i<>j then E[i,j]:=0 else E[i,i]:=1;
end;
{procedure UmnogMatr(A,F:mas; Var R:mas; n:byte);
Var s:real;
l,i,j:byte;
begin
for i:=1 to n do
for j:=1 to n do
begin
s:=0;
for l:=1 to n do
s:=s+A[i,l]*F[l,j];
R[i,j]:=s;
end;
end; }
begin
writeln('Vvedite razmernost` matrici A');
readln(ww);
f:=ww;
n1:=ww;
for i:=1 to ww do
begin
for j:=1 to ww do
begin
write('a[',i,j,']=');
Readln(A[i,j]);
A1[i,j]:=A[i,j];
end;
end;
q:=1;
x:=0;
dan(ww,a);
for i:=1 to q-1 do
writeln('Koren` har-ogo ur-iya=',o[i]:2:2);
writeln;
i:=ww+1;
if (x=1)or(x>1) then
begin
for v:=1 to x do
begin
tt:=0;
repeat
tt:=tt+1;
i:=i-1;
until t[i]<>false;
write('l^',tt,' + ');
for jj:=ww downto i do
begin
tt:=tt-1;
write(-p[jj]:2:2,'*l^',tt,' + ');
end;
ww:=i-1;
writeln;
end;
end;
for i:=1 to n1 do
begin
for j:=1 to n1 do
read(R[i,j]);
readln;
end;
EdMatr(R1,n1);
ObrMatr(R,R1,n1);
Umnogenie(R1,A1,n1,A);
Umnogenie(A,R,n1,M1);
for i:=1 to n1 do
begin
for j:=1 to n1 do
write(' ',M1[i,j]:2:3,' ');
writeln;
end;
end.
Анализ программыПротестируем работу программы на примере. Пусть имеем матрицу А
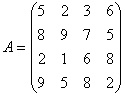
Характеристический полином имеет вид:![]()
Собственные числа 20.713, 4.545, 2.556, -5.814
Собственные векторы  ,
, 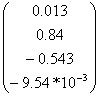 ,
, ,
,
Список используемой литературы
Я.М.Григоренко, Н.Д.Панкратова «Обчислювальні методи» 1995р.
В.Д.Гетмнцев «Лінійна алгебра і лінійне програмування» 2001р.
Д.Мак-Кракен, У.Дорн «Программирование на ФОРТРАНЕ» 1997г.
http://alglib.manual.ru/eigen/danilevsky.php
http://doors.infor.ru/allsrs/alg/index.html
Похожие работы
... XBIG XL = XBIG RETURN END {**********************************************************************} Результат работы программы получаем в виде: Номер Итерации Собственное Значение ( N / M ** 2 ) Собственный вектор X (1) X (2) X (3) 0. 1.00000 0. 0. 0.10000 Е 08 1,00000 0.50000 0.60000 0.26000Е 08 0.61923 0.66923 1.00000 0.36392Е ...
... RETURN END {**********************************************************************} Результат работы программы получаем в виде: Номер Итерации Собственное Значение ( N / M ** 2 ) Собственный вектор X (1) X (2) X (3) 0. 1.00000 0. 0. 1. 0.10000 Е 08 1,00000 0.50000 0.60000 2. 0.26000Е 08 0.61923 0.66923 ...
... лежащие на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
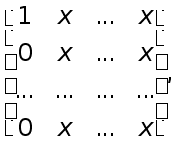
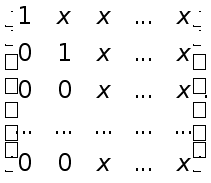
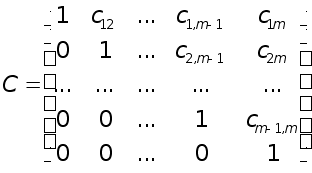

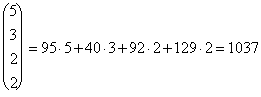

0 комментариев