Навигация
Математическая модель установки и преобразование ее в пространство состояний
2 Математическая модель установки и преобразование ее в пространство состояний
Математическая модель в виде матрицы передаточных функций приведена в таблице 2.
Таблица.2
| u1, м3/с , брага | u2, кг/с, пар | |
|
|
|
|
| y2, 0.7+-0.05 |
|
|
На рисунке 2 представлена блок – схема модели колонны.
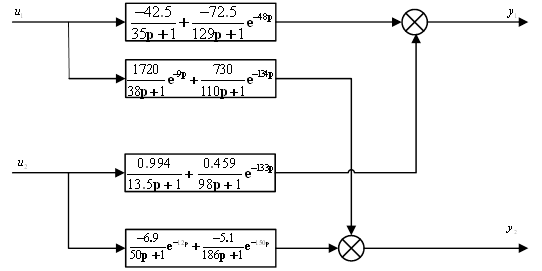
Рисунок 2 – Блок-схема модели колонны
В исходных данных, модель дана как мы видим в виде матриц передаточных фунцый. Для преобразования передаточных функций в пространство состояний использовали соотношения. Наиболее простой аппроксимацией опоздания является замена его инерционным звеном первого порядка. Для проверки правильности преобразования следует найти собственные значения системы с помощью функции Eig и убедиться, что или все собственные значения имеют отрицательные действительные части (система постоянна), или число нулевых собственных значений совпадает с числом интегральных звеньев в исходной модели. Окончательно система должна быть представлена матрицами A,B,C,D.
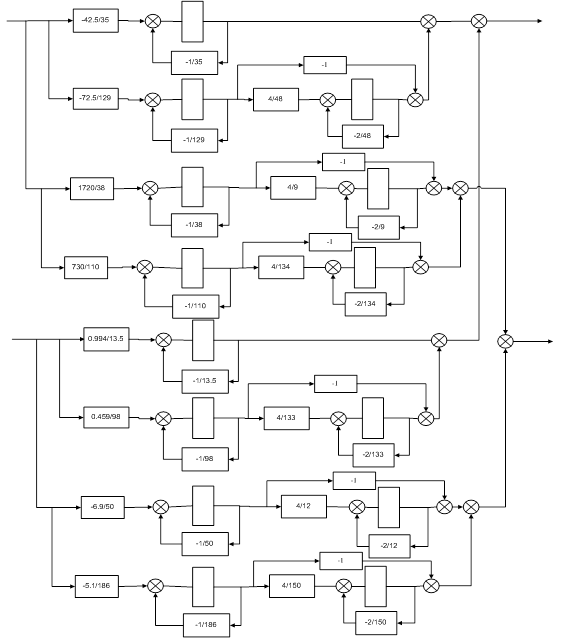
| |
| |
Рисунок 3. Развернутая структурная схема системы с учетом запаздывания
Исходя из систем получим матрицы модели в пространстве состояний
![]()
где х- состояние систем;
y- измеряемые входы;
f- возмущение;
u- управление.
Матрицы системы имеют вид:
A=[-1/35 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 -1/129 0 0 0 0 0 0 0 0 0 0 0 0;
0 4/48 -2/48 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 -1/38 0 0 0 0 0 0 0 0 0 0;
0 0 0 4/9 -2/9 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 -1/110 0 0 0 0 0 0 0 0;
0 0 0 0 0 4/134 -2/134 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 -1/13.5 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 -1/98 0 0 0 0 0;
0 0 0 0 0 0 0 0 4/133 -2/133 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 -1/50 0 0 0;
0 0 0 0 0 0 0 0 0 0 4/12 -2/12 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 -1/186 0;
0 0 0 0 0 0 0 0 0 0 0 0 4/150 -2/150];
Матрица входа:
B=[-42.5/35 0;
-72.5/129 0;
0 0;
1720/38 0;
0 0;
730/110 0;
0 0;
0 0.994/13.5;
0 0.459/98;
0 0;
0 -6.9/50;
0 0;
0 -5.1/186;
0 0];
Матрица измерений:
C=[1 -1 1 0 0 0 0 1 -1 1 0 0 0 0;
0 0 0 -1 1 -1 1 0 0 0 -1 1 -1 1];
где матрица системы:
D=[0 0;0 0];
3 Преобразование математической модели в дискретное время и ее проверка с помощью построения разгонных характеристик
Для преобразования математической модели в дискретное время использовалась функция программного пакета Matlab c2d. При этом шаг дискретности нужно выбирать с учетом того что процессы в замкнутой системе будут проходить в 10 раз быстрее чем в объекте.
dt=0.01/max(abs(eig(A)))
t=0:dt:999;
[Ad,Bd]=c2d(A,B,dt);
dt=0.4500
Проверить найденную модель в дискретном времени следует с помощью расчета разгонных характеристик. Для этого следует использовать функцию dstep. Для вывода графиков следует использовать функции: subplot, plot, grid.
Ad =
Columns 1 through 8
0.9872 0 0 0 0 0 0 0
0 0.9965 0 0 0 0 0 0
0 0.0371 0.9814 0 0 0 0 0
0 0 0 0.9882 0 0 0 0
0 0 0 0.1892 0.9048 0 0 0
0 0 0 0 0 0.9959 0 0
0 0 0 0 0 0.0134 0.9933 0
0 0 0 0 0 0 0 0.9672
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Columns 9 through 14
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0.9954 0 0 0 0 0
0.0135 0.9933 0 0 0 0
0 0 0.9910 0 0 0
0 0 0.1439 0.9277 0 0
0 0 0 0 0.9976 0
0 0 0 0 0.0119 0.9940
Bd =
-0.5429 0
-0.2525 0
-0.0047 0
20.2483 0
1.9628 0
2.9803 0
0.0200 0
0 0.0326
0 0.0021
0 0.0000
0 -0.0618
0 -0.0045
0 -0.0123
0 -0.0001
Построим разгонные характеристики с помощью функций dstep, subplot, plot, grid.
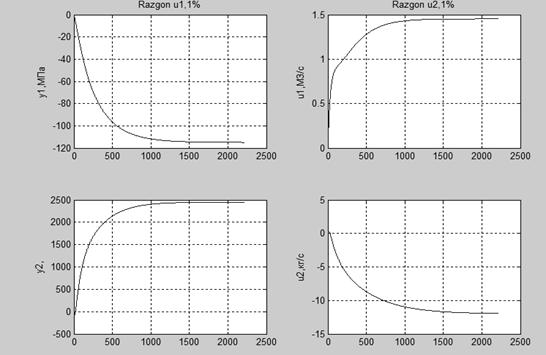
Рисунок 4.Кривые разгона.
В результате анализа кривых разгона можно сделать вывод, что значения полученные на выходе каналов регулирования описанных инерционными звеньями 1-го порядка совпадают со значением коэффициента К инерционного звена, а на выходе каналов регулирования представленных интегрирующим звеном, кривые разгона направлены в отрицательную сторону, если имеют знак «-» в передаточной функции звена и наоборот. Если сравнить матрицу передаточных функций и полученные разгонные характеристики, видно, что Кр совпадают, можно сделать вывод: построение модели и преобразование выполнены верно.
4 Синтез многомерного ПИ-регулятора
Для синтеза ПИ-регулятора полученные матрицы должны быть расширены в матрицы A1, B1, C1:
A1=[Ad zeros(n,l); C eye(l)];
B1=[Bd;zeros(m)];
C1=[C eye(l)];
Матрицы параметров регулятора должны быть расчитаны с помощью функции dlqr.
K=dlqr(A1,B1,Q,R)
L=dlqr(A1',C1',Q1,R1)'
Весовые матрицы Q1,R1,Q,R выбраны как единичные (для простоты матрицы генерирует функция eye).
Матрицы имеют вид:
A1 =
Columns 1 through 8
0.9872 0 0 0 0 0 0 0
0 0.9965 0 0 0 0 0 0
0 0.0371 0.9814 0 0 0 0 0
0 0 0 0.9882 0 0 0 0
0 0 0 0.1892 0.9048 0 0 0
0 0 0 0 0 0.9959 0 0
0 0 0 0 0 0.0134 0.9933 0
0 0 0 0 0 0 0 0.9672
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
1.0000 -1.0000 1.0000 0 0 0 0 1.0000
0 0 0 -1.0000 1.0000 -1.0000 1.0000 0
Columns 9 through 16
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0.9954 0 0 0 0 0 0 0
0.0135 0.9933 0 0 0 0 0 0
0 0 0.9910 0 0 0 0 0
0 0 0.1439 0.9277 0 0 0 0
0 0 0 0 0.9976 0 0 0
0 0 0 0 0.0119 0.9940 0 0
-1.0000 1.0000 0 0 0 0 1.0000 0
0 0 -1.0000 1.0000 -1.0000 1.0000 0 1.0000
B1 =
-0.5429 0
-0.2525 0
-0.0047 0
20.2483 0
1.9628 0
2.9803 0
0.0200 0
0 0.0326
0 0.0021
0 0.0000
0 -0.0618
0 -0.0045
0 -0.0123
0 -0.0001
0 0
0 0
C1 =
Columns 1 through 13
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
Columns 14 through 16
0 1 0
0 0 1
K =
Columns 1 through 8
0.0367 -0.0578 0.0407 0.0634 0.0239 -0.0813 0.1013 0.0485
21.0412 -24.2138 21.6345 4.5472 11.1495 -21.5375 25.0390 22.7474
Columns 9 through 16
-0.0419 0.0319 0.0446 0.0349 -0.0865 0.1026 0.0000 0.0001
-21.8436 20.3135 0.9756 13.2017 -22.4572 25.2658 0.0195 0.0270
L =
0.0925 -0.0000
0.1180 0.0000
0.3752 0.0000
0.0000 0.0568
0.0000 0.1807
0.0000 0.0279
-0.0000 0.2379
0.0694 -0.0000
0.0275 0.0000
0.2971 0.0000
-0.0000 0.0629
-0.0000 0.1964
0.0000 0.0673
0.0000 0.3243
1.6139 0.0000
0.0000 1.6702
5 Моделирование замкнутой системы и оценка качества переходных процессов
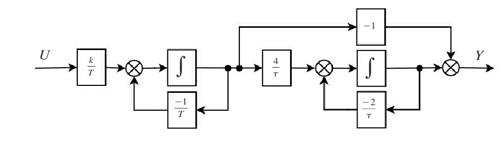
Рисунок 5 – Структурная схема системы в виде переменных состояния с учетом запаздывания.
Для получения переходных процессов следует сформировать матрицы замкнутой системы и получить переходные процессы с помощью программы dstep .
AA=[A1 -B1*K;L*C1 A1-B1*K-L*C1];
BB=[B1;zeros(n+l,m)];
CC=[C zeros(l) zeros(l,n+l)];
При оценке качества переходных процессов необходимо чтоб управляющее воздействие не превышало 100% открытия.
Максимальное возмущение следует принять на уровне 10% номинального значения соответствующих параметров. Допустимое значение урегулированных переменных нужно принять равными 20% номинального значения. Если качество не соответствует нужно сменить весовые матрицы и повторить расчет.
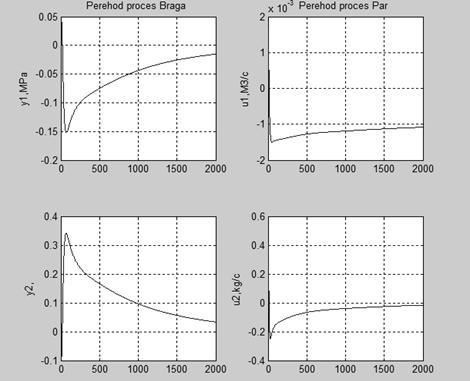
Рисунок 6.Переходные процессы замкнутой системы.
Проанализировав переходные процессы можно сделать вывод, что значения регулируемых параметров не превышают допустимых. Для определения времени регулирования нужно количество итераций цикла умножить на шаг: ![]() .
.
Похожие работы
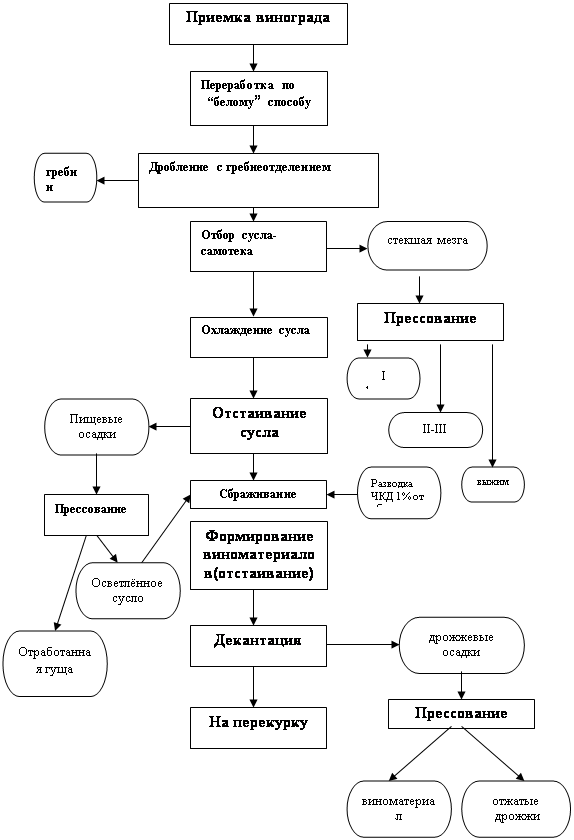
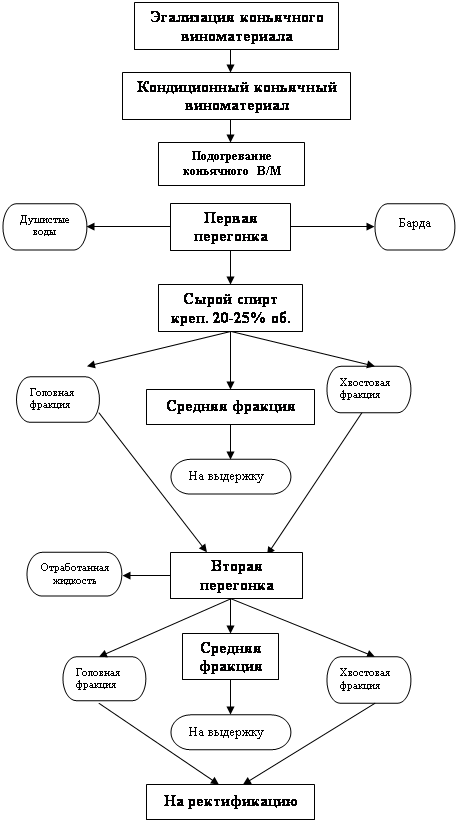
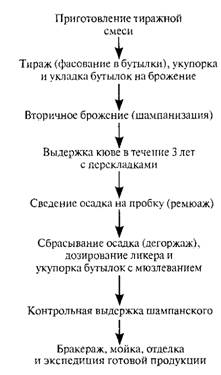
... сусло направляют на брожение. Брожение производят без применения диоксида серы периодическим способом в резервуарах различной вместимости или непрерывным способом в линиях непрерывного сбраживания различных модификаций.. Использование различных перегонных установок и технологий получения коньячного спирта оказывает существенное влияние на технико-экономические показатели дистилляции ( табл. 1 ). ...
... 1,0 1,0 1,0 1,0 1,0 1,0 Массовая концентрация меди, мг/дм3, не более 5 5 5 5 5 5 Массовая концентрация железа, мг/дм3, не более 1,5 1,5 1,5 1,5 1,5 1,5 Содержание токсичных элементов в коньяке не должно превышать допустимые уровни, установленные «Гигиеническими требованиями безопасности и пищевой ценности пищевых продуктов» Сан-ПиН 2.3.2.1078-01. 2. Производство ...
... экспериментально измеренная хроматограмма стандартного образца состава раствора токсичных микропримесей в водно-спиртовой смеси. Метрологические характеристики измеренного образца также представлены в приложении А [6]. 3.2 Проверка водки на крепость В мерную колбу вместимостью 200–250 см3 отмеривают исследуемый продукт до метки при температуре 20 °С. Затем продукт переносят из мерной колбы ...
... крупнейших открытий, выполненных А.М. Фроловым-Багреевым, явилась разработка проблемы шампанизации вина в крупных резервуарах. За разработку и широкое внедрение в промышленность отечественной технологии производства шампанских вин резервуарным способом А.М. Фролов-Багреев был удостоен в 1942 году Сталинской премии. Ему принадлежит также большая заслуга в организации научно-производственной школы ...
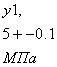

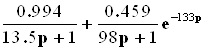
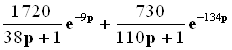

0 комментариев