Аналіз енергетичного комплексу України
Огляд публікацій за напрямком роботи
Постановка задачі побудови комплексу моделей енергоспоживання регіонів
Застосування методів багатовимірного статистичного аналізу в моделюванні енергоспоживання
Метод аналізу із застосуванням карт Кохонена
Моделі аналізу регіонів України за енергоспоживанням
Моделі оцінки регіонального енергоспоживання
Навигация
Метод аналізу із застосуванням карт Кохонена
Комплекс моделей енергоспоживання регіонами України
127126
знаков
10
таблиц
37
изображений
2.3 Метод аналізу із застосуванням карт Кохонена
Аналізуючи найбільш відомі на даний час розробки нейромереж, слід зазначити, що самим поширеним варіантом архітектури є багатошарові мережі зазначені на рис. 2.3. Нейрони в даному випадку об'єднуються у прошарки з єдиним вектором сигналів входів. Зовнішній вхідний вектор подається на вхідний прошарок нейронної мережі (рецептори). Виходами нейронної мережі є вихідні сигнали останнього прошарку (ефектори). Окрім вхідного та вихідного прошарків, нейромережа має один або декілька прихованих прошарків нейронів, які не мають контактів із зовнішнім середовищем.
Таким чином, звичайні нейронні мережі виявляють закономірності між вхідними даними і прогнозованою величиною. Якщо такі закономірності є, то нейромережа їх виділить, і прогноз буде успішним.
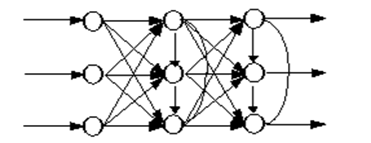
Рис. 2.3. Багатошаровий тип з'єднання нейронів
Мережі прямого поширення відносять до статичних, так як на задані входи нейронів надходить не залежний від попереднього стану мережі вектор вхідних сигналів. Рекурентні мережі вважаються динамічними, тому що за рахунок зворотних зв'язків (петель) входи нейронів модифікуються в часі, що приводить до змін станів мережі.
Оригінальність нейромереж, як аналога біологічного мозку, полягає у здібності до навчання за прикладами, що складають навчальну множину. Процес навчання нейромереж розглядається як налаштування архітектури та вагових коефіцієнтів синаптичних зв'язків відповідно до даних навчальної множини так, щоб ефективно вирішити поставлену задачу. Виділяють варіанти контрольованого та неконтрольованого навчання.
Величезна більшість рішень отримана від нейромереж з контрольованим навчанням, де біжучий вихід постійно порівнюється з бажаним виходом. Ваги на початку встановлюються випадково, але під час наступних ітерації коректуються для досягнення близької відповідності між бажаним та біжучим виходом. Створені методи навчання націлені на мінімізації біжучих похибок всіх елементів обробки, яке створюється за якийсь час неперервною зміною синаптичних ваг до досягнення прийнятної точності мережі.
Перед використанням, нейромережа з контрольованим навчанням повинна бути навченою. Фаза навчання може тривати багато часу, зокрема, у прототипах систем, з невідповідною процесорною потужністю навчання може займати декілька годин. Навчання вважається закінченим при досягненні нейромережею визначеного користувачем рівня ефективності. Цей рівень означає, що мережа досягла бажаної статистичної точності, оскільки вона видає бажані виходи для заданої послідовності входів. Після навчання ваги з'єднань фіксуються для подальшого застосування. Деякі типи мереж дозволяють під час використання неперервне навчання, з набагато повільнішою оцінкою навчання, що допомагає мережі адаптуватись до повільно змінюючихся умов.
Навчальні множини повинні бути досить великими, щоб містити всю необхідну інформацію для виявлення важливих особливостей і зв'язків. Але і навчальні приклади повинні містити широке різноманіття даних. Якщо мережа навчається лише для одного прикладу, ваги старанно встановлені для цього прикладу, радикально змінюються у навчанні для наступного прикладу. Попередні приклади при навчанні наступних просто забуваються. В результаті система повинна навчатись всьому разом, знаходячи найкращі вагові коефіцієнти для загальної множини прикладів. Наприклад, у навчанні системи розпізнавання піксельних образів для десяти цифр, які представлені двадцятьма прикладами кожної цифри, всі приклади цифри "сім" не доцільно представляти послідовно. Краще надати мережі спочатку один тип представлення всіх цифр, потім другий тип і так далі.
Головною компонентою для успішної роботи мережі є представлення і кодування вхідних і вихідних даних. Штучні мережі працюють лише з числовими вхідними даними, отже, необроблені дані, що надходять із зовнішнього середовища повинні перетворюватись. Додатково необхідне масштабування, тобто нормалізація даних відповідно до діапазону всіх значень. Попередня обробка зовнішніх даних, отриманих за допомогою сенсорів, у машинний формат спільна для стандартних комп'ютерів і є легко доступною.
Якщо після контрольованого навчання нейромережа ефективно опрацьовує дані навчальної множини, важливим стає її ефективність при роботі з даними, які не використовувались для навчання. У випадку отримання незадовільних результатів для тестової множини, навчання продовжується. Тестування використовується для забезпечення запам'ятовування не лише даних заданої навчальної множини, але і створення загальних образів, що можуть міститись в даних.
Неконтрольоване навчання може бути великим надбанням в майбутньому. Воно проголошує, що комп'ютери можуть самонавчатись у справжньому роботизованому сенсі. На даний час, неконтрольоване навчання використовується мережах відомих, як самоорганізовані карти (self organizing maps), що знаходяться в досить обмеженому користуванні, але доводячи перспективність самоконтрольованого навчання. Мережі не використовують зовнішніх впливів для коректування своїх ваг і внутрішньо контролюють свою ефективність, шукаючи регулярність або тенденції у вхідних сигналах та роблять адаптацію згідно навчальної функції. Навіть без повідомлення правильності чи неправильності дій, мережа повинна мати інформацію відносно власної організації, яка закладена у топологію мережі та навчальні правила.
Алгоритм неконтрольованого навчання скерований на знаходження близькості між групами нейронів, які працюють разом. Якщо зовнішній сигнал активує будь-який вузол в групі нейронів, дія всієї групи в цілому збільшується. Аналогічно, якщо зовнішній сигнал в групі зменшується, це приводить до гальмуючого ефекту на всю групу.
Конкуренція між нейронами формує основу для навчання. Навчання конкуруючих нейронів підсилює відгуки певних груп на певні сигнали. Це пов'язує групи між собою та відгуком. При конкуренції змінюються ваги лише нейрона-переможця.
Оцінка ефективності навчання нейромережі залежить від декількох керованих факторів. Теорія навчання розглядає три фундаментальні властивості, пов'язані з навчанням: ємність, складність зразків і обчислювальна складність. Під ємністю розуміють, скільки зразків може запам'ятати мережа, і які межі прийняття рішень можуть бути на ній сформовані. Складність зразків визначає число навчальних прикладів, необхідних для досягнення здатності мережі до узагальнення. Обчислювальна складність напряму пов'язана з потужністю процесора ЕОМ.
У загальному використанні є багато правил навчання, але більшість з цих правил є деякою зміною відомого та найстаршого правила навчання, правила Хеба. Дослідження різних правил навчання триває, і нові ідеї регулярно публікуються в наукових та комерційних виданнях. Представимо декілька основних правил навчання.
Правило Хеба з'явилося у його книзі "Організація поведінки" у 1949 р. "Якщо нейрон отримує вхідний сигнал від іншого нейрону і обидва є високо активними (математично мають такий самий знак), вага між нейронами повинна бути підсилена". При збудженні одночасно двох нейронів з виходами (хj, уі) на k-тому кроці навчання вага синаптичного з'єднання між ними зростає, в інакшому випадку - зменшується, тобто
D Wij(k)=r xj (k) yi (k),
де r - коефіцієнт швидкості навчання.
Правило Хопфілда є подібним до правила Хеба за винятком того, що воно визначає величину підсилення або послаблення. "Якщо одночасно вихідний та вхідний сигнал нейрона є активними або неактивними, збільшуємо вагу з'єднання оцінкою навчання, інакше зменшуємо вагу оцінкою навчання".
Правило "дельта". Це правило є подальшою зміною правила Хеба і є одним із найбільш загально використовуваних. Це правило базується на простій ідеї неперервної зміни синаптичних ваг для зменшення різниці ("дельта") між значенням бажаного та біжучого вихідного сигналу нейрона.
DWij= xj (di - yi).
За цим правилом мінімізується середньоквадратична похибка мережі. Це правило також згадується як правило навчання Відрова-Хофа та правило навчання найменших середніх квадратів.
У правилі "дельта" похибка отримана у вихідному прошарку перетворюється похідною передатної функції і послідовно пошарово поширюється назад на попередні прошарки для корекції синаптичних ваг. Процес зворотного поширення похибок мережі триває до досягнення першого прошарку. Від цього методу обчислення похибки успадкувала своє ім'я відома парадигма FeedForward BackPropagation.
При використанні правила "дельта" важливим є невпорядкованість множини вхідних даних. При добре впорядкованому або структурованому представленні навчальної множини результат мережі може не збігтися до бажаної точності і мережа буде вважатись нездатною до навчання.
Правило градієнтного спуску. Це правило подібне до правила "дельта" використанням похідної від передатної функції для змінювання похибки "дельта" перед тим, як застосувати її до ваг з'єднань. До кінцевого коефіцієнта зміни, що діє на вагу, додається пропорційна константа, яка пов'язана з оцінкою навчання. І хоча процес навчання збігається до точки стабільності дуже повільно, це правило поширене і є загально використовуване.
Доведено, що різні оцінки навчання для різних прошарків мережі допомагає процесу навчання збігатись швидше. Оцінки навчання для прошарків, близьких до виходу встановлюються меншими, ніж для рівнів, ближчих до входу.
На відміну від навчання Хеба, у якому множина вихідних нейронів може збуджуватись одночасно, при навчанні методом змагання вихідні нейрони змагаються між собою за активізацію. Це явище відоме як правило "переможець отримує все". Подібне навчання має місце в біологічних нейронних мережах. Навчання за допомогою змагання дозволяє кластеризувати вхідні дані: подібні приклади групуються мережею відповідно до кореляцій і представляються одним елементом.
При навчанні модифікуються синаптичні ваги нейрона-переможця. Ефект цього правила досягається за рахунок такої зміни збереженого в мережі зразка (вектора синаптичних ваг нейрона-переможця), при якому він стає подібним до вхідного приклада. Нейрон з найбільшим вихідним сигналом оголошується переможцем і має можливість гальмувати своїх конкурентів і збуджувати сусідів. Використовується вихідний сигнал нейрона-переможця і тільки йому та його сусідам дозволяється коректувати свої ваги з'єднань.
DWij (k+1)= Wij(k)+r [xj - Wij(k)].
Розмір області сусідства може змінюватись під час періоду навчання. Звичайна парадигма повинна починатись з великої області визначення сусідства і зменшуватись під час процесу навчання. Оскільки елемент-переможець визначається по найвищій відповідності до вхідного зразку, мережі Коxонена моделюють розподіл входів. Це правило використовується в самоорганізованих картах.
Розглядаючи карти Кохонена забражені на рис. 2.4., перш за все необхідно пригадати, що будь-яка нейронна мережа, перш за все, має бути виучена. Процес навчення полягає в підстроюванні внутрішніх параметрів нейромережі під конкретне завдання.
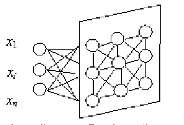
Рис. 2.4. Мережа Кохонена
При вченні «класичної» багатошарової нейромережі на вхід подаються дані або індикатори, а вихід нейромережі порівнюється з еталонним значенням (з так званим «вчителем»). Різниця цих значень називається помилкою нейронної мережі, яка і мінімізується в процесі вчення.
Таким чином, звичайні нейронні мережі виявляють закономірності між вхідними даними і прогнозованою величиною. Якщо такі закономірності є, то нейромережа їх виділить, і прогноз буде успішним [26].
В процесі навчання карт Кохонена на входи також подаються дані і індикатори, але при цьому мережа підстроюється під закономірності у вхідних даних, а не під еталонне значення виходу. Таке вчення називається вченням «без вчителя». Вчення при цьому полягає не в мінімізації помилки, а в підстроюванні внутрішніх параметрів нейромережі (вагів) для великого сов падіння з вхідними даними. Після вчення така нейромережа візуально відображує багатовимірні вхідні дані на плоскості нейронів.
Маючи таке представлення даних, можна дуже наочно побачити наявність або відсутність взаємозв'язку у вхідних даних. Для великої зручності візуальної вистави нейрони карти Кохонена розташовують у вигляді двомірної матриці і розфарбовують цю матрицю залежно від аналізованих параметрів нейронів
При роботі із звичайними нейромережами, операція картами Кохонена складається з декількох послідовних етапів.
Першим з них є етап визначення складу входів.Для хорошого вчення звичайної нейромережі потрібно вибрати таку безліч входів, яка найсильніше впливає на вихідні (прогнозовані) значення. Якщо ми вгадали, і входи дійсно впливають на виходи, то нейромережа працюватиме і даватиме відмінні прогнози. Проте підібрати правильні входи дуже складно. Зазвичай це робиться методом проб і помилок, тобто простим перебором різних комбінацій індикаторів і даних [27].
Входи нейромережі, що виучується «без вчителя», визначаються іншим чином, і перед такою нейромережею ставиться інша мета - виявлення закономірностей між будь-якими вхідними даними і індикаторами, які і подаються на вхід карти.
Архітектура карт Кохонена, на відміну від багатошарової нейромережі, дуже проста і є один-єдиним шаром нейронів, який організований у вигляді двомірної матриці. Користувачеві необхідно визначити лише розмір цієї матриці, тобто кількість нейронів по ширині і кількість нейронів по висоті.
Карти Кохонена дають візуальне відображення багатовимірних вхідних даних. У картах Кохонена аналізуються не тільки виходи нейронів (як у віпадку звичайної нейромережі), але також ваги нейронів і розподілу прикладів по нейронах. Оскільки карта Кохонена організована у вигляді двомірних грат, у вузлах якої розташовуються нейрони, то її дуже зручно відображувати на плоскості у вигляді «карти» з розфарбовуванням, залежним від величини аналізованого параметра нейрона.Саме за схожість такого типу зображення нейромережі з топографічними картами вони отримали назву карт Кохонена.
Таким чином, карти Кохонена, що самоорганізующиеся, є одним з видів нейронних мереж. Принципи роботи і вчення такої нейромережі були сформульовані фінським ученим Тойво Кохоненом в 1982 році. Основною ідеєю Т. Кохонена є введення в правило вчення нейрона інформації про його розташування. По Кохонену, нейромережу має один вхідний шар, з числом нейронів, рівним числу входів, і єдиний прихований (вихідний) шар нейронів, створюючий одновимірні (лінія) або двомірні (прямокутник) грати. По аналогії з топографічними картами таку нейромережу також називають картою Кохонена [28].
Для цієї парадигми вчення проводиться без «вчителя», тобто в процесі вчення немає порівняння виходів нейронів з еталонними значеннями.
В процесі навчання на вхід такої нейромережі поступово подаються навчальні приклади. Після подачі чергового прикладу визначається найбільш схожий нейрон, тобто нейрон, у якого скалярний добуток вагів і поданого на вхід вектора мінімально. Такий нейрон вважається переможцем і покликаний бути центром при підстроюванні вагів у сусідніх нейронів.
Правило вчення, запропоноване Кохоненом, передбачає змагання з врахуванням відстані нейронів від «нейрона-переможця.
Для нейрона-переможця функція сусідства дорівнює 1 і потім плавно (по лінійному або експоненціальному закону) зменшується при видаленні від нього. Таким чином, в процесі вчення підстроювання вагів відбувається не лише в одному нейроні - нейроні-переможцеві, але і в його околицях.
Після закінчення процесу вчення карта Кохонена класифікує вхідні приклади на групи схожих один з одним. Вся сукупність нейронів у вихідному шарі точно моделює структуру розподілу повчальних прикладів в багатовимірному просторі. Унікальність технології карт, що самоорганізующихся, полягає в перетворенні N-мерного простори в двух- або одновимірне. Єдине, що треба пам'ятати, - таке перетворення зв'язане з деякими помилками. Дві крапки, близько лежачі на карті Кохонена, будуть близькі і в N-мерном вхідному просторі, але не навпаки.
Для кращого розуміння надається приклад, що роз'яснює спільні підходи до аналізу карт, що самоорганізующихся. Подамо на два входи карти (розміром 50х50 нейронів) набір випадкових чисел від 0 до 50 спільним числом 500 прикладів.
Після проведення вчення такої карти Кохонена все сімейство карт матиме вигляд, змальований на малюнку. Карта частот має рівномірний розподіл прикладів по поверхні карти, що пояснюється рівномірним розподілом вхідних прикладів і якістю вчення карти.
Для нас в даному прикладі представляє інтерес розфарбовування карти входів. Розфарбовування кожною з них лінійна і постійна по одній з граней карти. Причому обидві карти входів мають однакове розфарбовування, але розгорнені один відносно одного на 90 градусів. Як це можна трактувати? При значенні 1- го входу, рівного 0 (темно-синя смуга на першій карті), 2-й вхід може приймати весь спектр значень від 0 (темно-синій) до 50 (темно-червоний). Це відповідає вхідному розподілу даних (пара незалежних, рівномірно розподілених величин). Таким чином, карта, що самоорганізующаяся, змогла правильно відображувати взаємний розподіл двох входів карти.
Виходи нейронів карти Кохонена нагадують топографічну карту. Координати цієї карти визначають положення одного нейрона. Наприклад, координати 12:34 описують нейрон, що знаходиться на пересіченні 12 стовпця з 34 поруч в матриці нейронів. Величина виходу нейрона по аналогії з географічними картами трактується як висота крапки.
Карти Кохонена, так само як і географічні карти, можна відображувати або в двомірному, або тривимірному вигляді. У двомірному вигляді карта розфарбовується відповідно до рівня виходу нейрона.
Для вищих значень зазвичай використовуються світлі тони, а для низьких значень - темні.
Карта виходів є головною картою в аналізі карт Кохонена. Саме на неї проектується взаємне розташування досліджуваних даних. Схожі вхідні дані утворюють на карті кластери - замкнуті області, що складаються з нейронів з однаковими значеннями виходів. Як правило, яскраво виражені кластери в даних мають чіткі кордони з іншими областями карти. У тривимірному вигляді це виглядає як крутий схил горба.
Після завершення вчення кожен вхідний приклад потрапляє в «свій» нейрон. При цьому в деякі нейрони не попаде жодного прикладу, а в деяких попаде декілька прикладів. Розподіл повчальних прикладів по нейронах дуже показово і відображується на карті частот.
У спільному випадку вхідні приклади рівномірно розподіляються по карті. Але якщо в даних є яскраво виражені групи, то приклади розподіляються нерівномірно, утворюючи кластери. Кластером може бути або відособлена група з декількох нейронів, в яку попало деяке число вхідних прикладів, або окремий нейрон, в який попало велике число вхідних прикладів.
Як говорилося вище, при аналізі карт Кохонена проводиться оцінка не лише виходів нейронів, але також і вагів нейронів.
Для кажного входу нейрона складається своя карта, яка розфарбовується у відповідності зі значенням відповідної нейрона. У нейронної мережі, навчаємої зі вчителем, ваги нейронів не мають фізичного сенсу і не використовуються в аналізі. При вченні ж без «вчителя» ваги нейронів підстроюються під точні значення вхідних змінних і відображають їх внутрішню структуру. Для ідеально вивченої нейронної мережі вага нейрона рівна відповідною компоненті вхідного прикладу. Зазвичай аналізують одночасно декілька карт входів. Спочатку на одній карті виділяють області однакового кольору. У цій області групуються вхідні приклади, що мають однакове значення відповідного входу. Далі нейрони з цієї області вивчаються на інших картах на предмет колірного розподілу.
При роботі з картами Кохонена важливо розуміти, що всі розглянуті вище карти - не більше ніж розфарбовування одних і тих же нейронів. При цьому кожен навчальний приклад має одне і те ж розташування на кожній з розглянутих карт.
В результаті проведення аналізу методів, що можуть бути примінені в сфері енергоспоживання, були виділені методи багатомірного статистичного аналізу для оцінки регіонального споживання енергоресурсів, а токож карти Кохонена для проведення кластеризації.
При визначенні пріоритетних напрямів комплексного енергоспоживання регіону кластерний аналіз може використовуватися в декількох аспектах. Перша сфера застосування - це виявлення проблем, формування переліку регіонів з високими показниками споживання ресурсів, наявності великих родовищ, заводів, які визначають загальні витрати енергоресурсів. Другим аспектом аналізу є оцінка потенціалу і відбір регіонів, які можуть стати "локомотивами" споживання, на основі вивчення розподілу ресурсів, виробничих потужностей.
Для того щоб оцінити регіони по їх енергоспоживанню була обрана модель дискримінантного аналізу, що дасть змогу при спостереженні великих статистичних сукупностей, як у даному випадку з регіонами, розділити неоднорідну сукупність на однорідні групи (класи). Таке розчленовування надалі при проведенні статистичного аналізу дає кращі результати моделювання залежностей між окремими ознаками.
Розділ 3. Моделювання та аналіз енергоспоживання регіонами України
Похожие работы
... . Деякі американські фірми купують устаткування для АЕС навіть в Японії! США не побудували жодного реактора за останні десять років. [48] РОЗДІЛ ІІ ГОЛОВНІ ФАКТОРИ ЕНЕРГЕТИЧНОЇ БЕЗПЕКИ США 2.1. Геополітичні плани США На початку ХХ століття коли США почали перетворюватися в одну з ведучих держав світу, ідеологи американського гегемонізму заявили про зазіхання США на панування у всьому ...
... ізації відтворювальних процесів в Україні. // Природа людини і динаміка соціально-економічних процесів: Зб. статей, вип.1,- Д.: Наука і освіта, - 1998. – С. 45. 49. Бачевська Ж. Проблеми правового регулювання інвестиційної діяльності.// Економіка, фінанси, право. - 1997. - №8. – С. 16-20. 50. Безуглий А.А. Вплив амортизаційної політики на прибуток і доходи бюджету // Фінанси України. - 2000. ...
... , підприємницьких структур різних форм власності, що зумовлює становлення місцевих бюджетів як важливого фінансового інструменту регулювання господарського і соціального життя. Важливим при оцінці ролі місцевих бюджетів у соціально-економічному розвитку регіонів є аналіз співвідношення обсягів місцевих бюджетів із загальними витратами зведеного бюджету (таблиця 31.2) Таблиця 31.2 Співвідношення ...
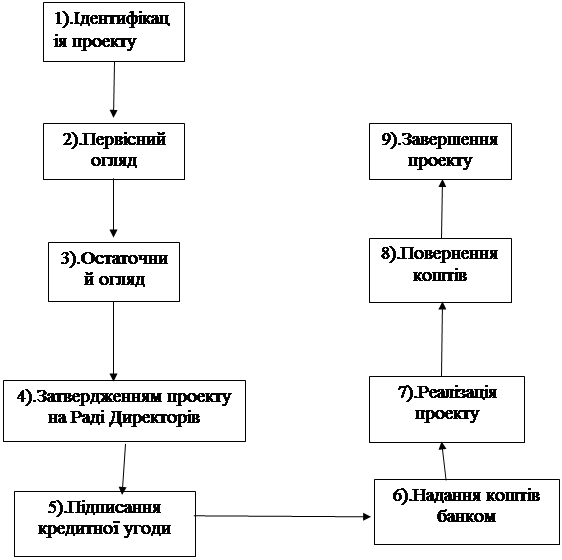
... Відсотки за кредити враховують можливість їхнього неповернення. Банк вимагає від компаній страхувати свої ризики, якщо це можливо. Слід відзначити, що, використовуючи різноманітні механізми фінансування, Європейський банк реконструкції та розвитку за час свого існування досяг значних результатів, особливо в країнах Центральної Європи – Польщі, Чехії, Словаччині, Угорщині, а також в прибалтійських ...
0 комментариев