Навигация
2. Конечные разности
2.1 Определение конечных разностей
Конечная разность «вперед» для таблично заданной функции в i-той точке определяется выражением: 
, где функция 
задана, как функция целочисленного аргумента с единичным шагом по аргументу i.
Для аналитически заданной и протабулированной с постоянным шагом h функции 
определяющее соотношение имеет вид:
.
Преобразование таблицы функции в функцию целочисленного аргумента осуществляют при помощи линейного соотношения между аргументами x и i: 
.
Коэффициенты a и b находят из системы уравнений, получаемой в результате подстановки в пределах заданной таблицы вместо x и i сначала начальных значений аргументов 
, а затем конечных 
. При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом
(
). Тогда для таблицы с (n+1) – й строками:
,
Повторные конечные разности n-го порядка в i-той точке для табличной функции определяются соотношением
.
2.2 Конечно-разностные операторы
Линейность конечно-разностного оператора 
позволяет ввести конечно-разностный оператор сдвига 
и многочлены от оператора с целыми коэффициентами, такие, как 
, где 
должно рассматриваться как оператор повторной разности k-того порядка.
Действие любого многочлена 
на функцию g(i) определяется как
.
Применение оператора сдвига к g(i) преобразует последнее в g (i+1):
g (i+1) = E g(i) = (1+) g(i)= g(i) + g(i).
Повторное применение оператора сдвига позволяет выразить (i+n) – е значение ординаты функции g через конечные разности различных порядков:
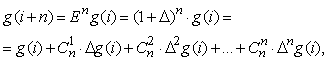
где 
– число сочетаний из n элементов по k;
– многочлен степени k от целой переменной n (
), имеющий k сомножителей. При k=n 
.
В силу линейности оператора сдвига можно конечно-разностный оператор выразить, как 
, и определить повторные конечные разности через многочлены от операторов сдвига так 
.
Последнее позволяет формульно выражать n-ную повторную разность через (n+1) ординату табличной функции, начиная с i-той строки:
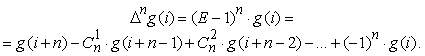
Если в выражении для g (i+n) положить i=0 и вместо 
подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам 
, которые в литературе называют факториальными:
.
Можно поставить задачу разложения и функции действительной переменной f(x) по многочленам 
относительно начала координат (аналогично ряду Маклорена), т.е. 
. Если последовательно находить конечные разности от левой и правой частей, то, зная, что 
и 
, после подстановки x=0 будем получать выражения для коэффициентов разложения 
. У многочленов k-той степени, 
, поэтому
.
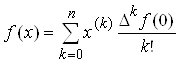Такое разложение табличной функции f(x) в литературе называют интерполяционным многочленом Ньютона для равных интервалов.
Похожие работы
... - - - 0 - - - 1 - - - В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона. 4.2 Рекуррентные формулы Адамса Пусть теперь требуется найти решение уравнения . для которого уже каким-либо способом найдены k+1 значений решения , что, естественно, определяет и ...
... неизвестных и матрица этой системы является трехдиагональной. Преобразуем уравнения (2.28): . (2.30) Введя обозначения получим , (i=0, 1,..., n-2). (2.31) Краевые условия по-прежнему запишем в виде . (2.32) Метод прогонки состоит в следующем. Разрешим уравнение (2.31) относительно : . (2.33) Предположим, что с помощью полной системы (2.31) из уравнения исключен член ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
... калькуляции представлены в табл.4.2. Ленточный график работ 5. Безопасность жизнедеятельности и охрана труда Дипломная работа посвящена анализу погрешностей волоконно-оптического гироскопа. В ходе ее выполнения были проведены необходимые расчеты и сделаны выводы, которые могут послужить материалом для ...
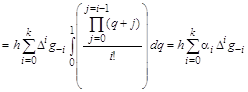
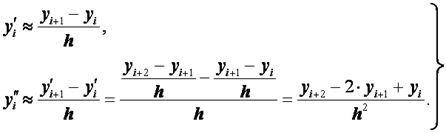
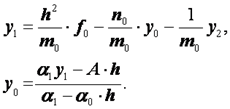
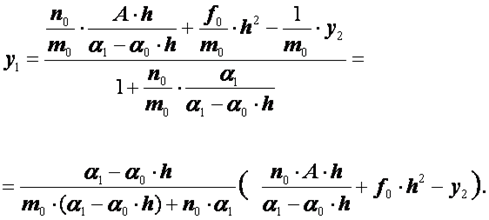
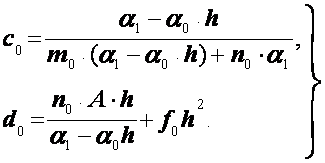
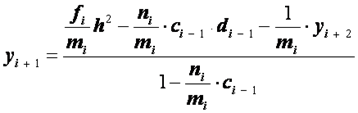
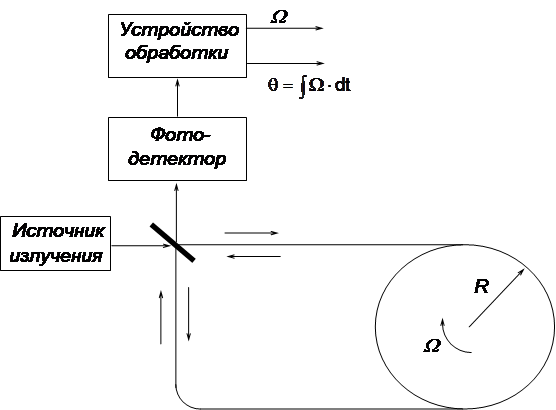
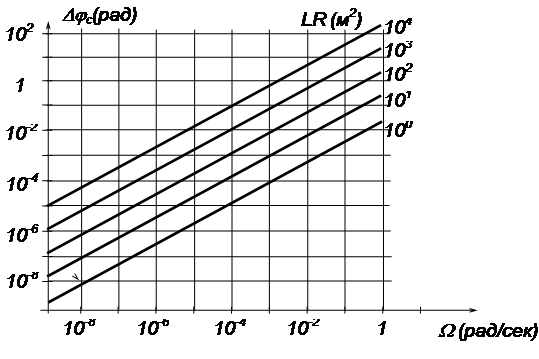
0 комментариев