Навигация
Математические методы в экономике
10815
знаков
10
таблиц
3
изображения
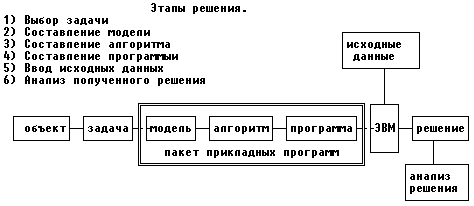
Задание 1. Графоаналитический метод решения задач линейного программирования
Постановка задачи: Необходимо найти решение задачи, состоящей в определении максимального значения функции F=c1x1+c2x2, где переменные xj≥0 (j=1;2) – планируемое количество единиц j-й продукции, а сj – прибыль на единицу j-й продукции при условиях ai1x1+ai2x2≤bi (i=1,…,k), xj≥0 (j=1,2).
Решение
1. Заменяем ограничения-неравенства на ограничения-равенства (привести задачу к каноническому виду).
2. Построим прямые, соответствующие полученным уравнениям.
3. Определить полуплоскости, соответствующие заданным неравенствам в системе ограничений.
4. Поиск области допустимых решений задачи.
5. Построить градиент функции цели: grad F=(F’x1; F’x2).
6. Построить прямую нулевого уровня c1x1+c2x2=0, (эта прямая перпендикулярна градиенту).
7. Переместить эту прямую в направлении градиента, в результате чего будет найдена точка (точки), в которой целевая функция принимает максимальное значение, или же установлена неограниченность функции на множестве планов.
8. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.
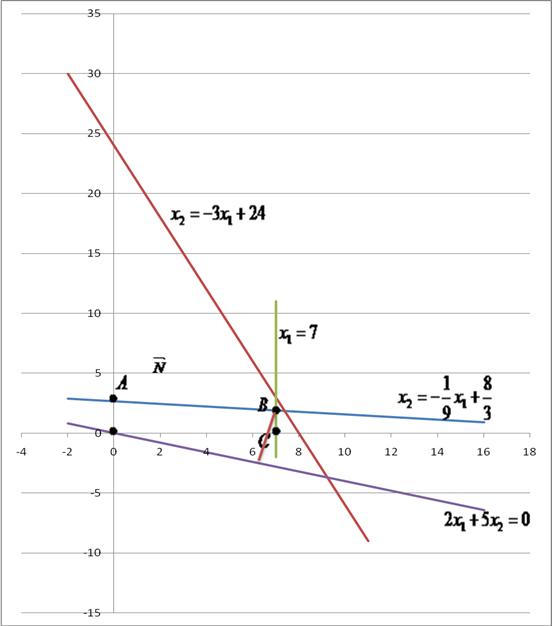
Система ограничений:
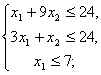
Целевая функция 
.
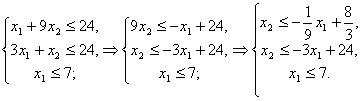(1)
Построим прямые, ограничивающие многоугольник допустимых решений:
|
|
|
- прямая, параллельная оси 
.
- линия уровня (F=0); 
|
| 0 | 5 |
|
| 0 | -2 |
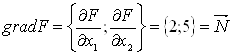- вектор, в направлении которого расположено оптимальное решение задачи
Из системы неравенств (1) следует, что многоугольник решений на графике ОАВС.
Максимальную длину имеет перпендикуляр, опущенный из точки В, где пересекаются прямые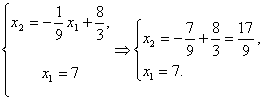 
- оптимальный план выпуска продукции.
- максимальное значение прибыли.
Задание 2. Симплекс-метод решения задач линейного программирования
Постановка задачи: необходимо найти решение задачи, состоящей в определении максимального значения функции F=c1x1+c2x2+c3x3, где переменные xj≥0 (j=1;2) – планируемое количество единиц j-й продукции, а сj прибыль на единицу j-й продукции при условиях ai1x1+ai2x2+…+ ainxn≤bi (i=1,…,m), xj≥0 (j=1,2,…,m).
Решение.
Похожие работы
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...
... + 6y ≤ b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Дать определение умножения матрицы на число. 2) Записать общую задачу ...
... ряд соображений, которые этим расчетом не были учтены. В зависимости от того, какой информацией обладают руководитель и его сотрудники, подготавливающие решения, меняются и условия принятия решений и математические методы, применяемые для выработки рекомендаций. Если известны все действующие в системе факторы, то есть отстствуют случайные воздействия, то это будет принятие решений в ...
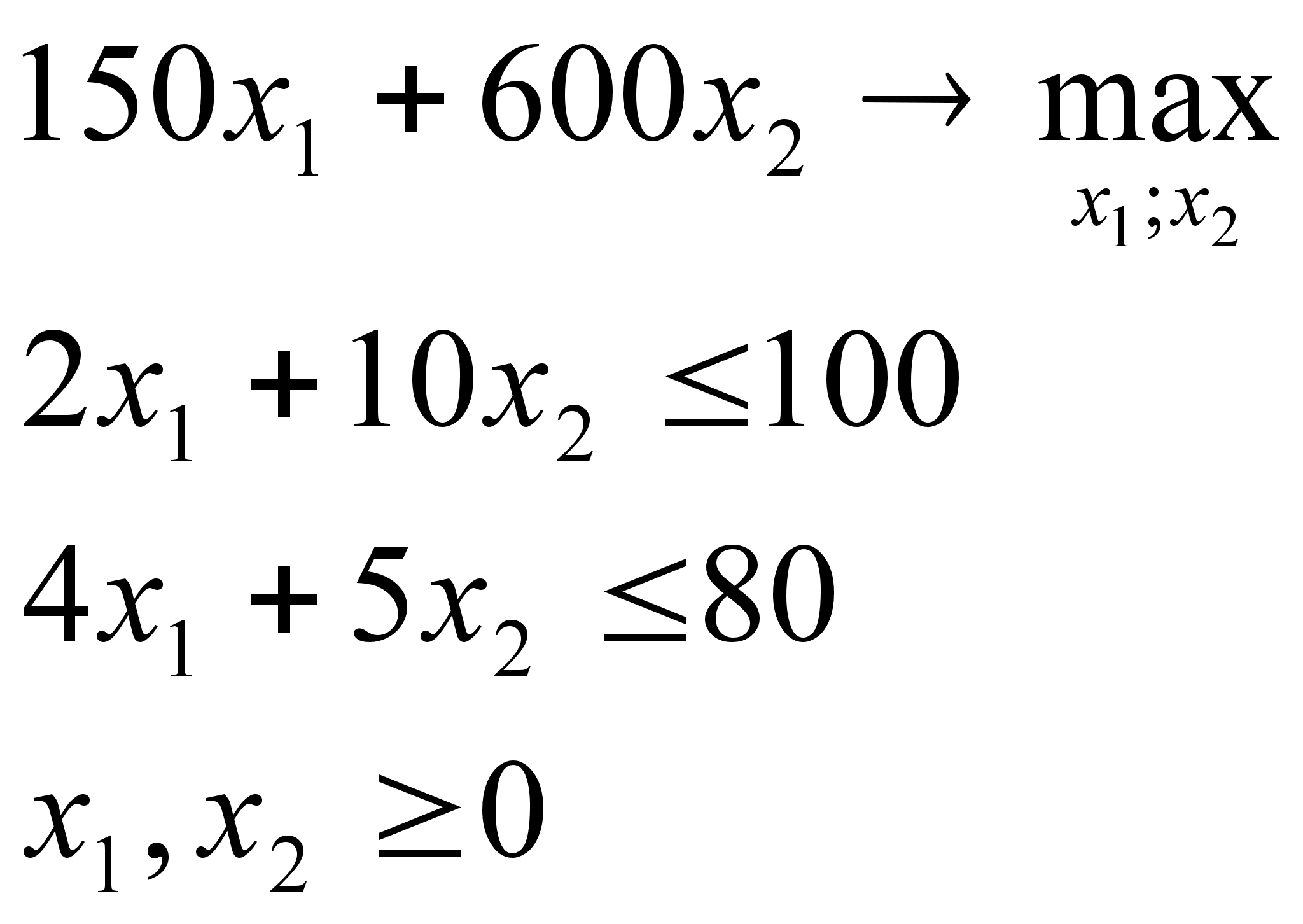
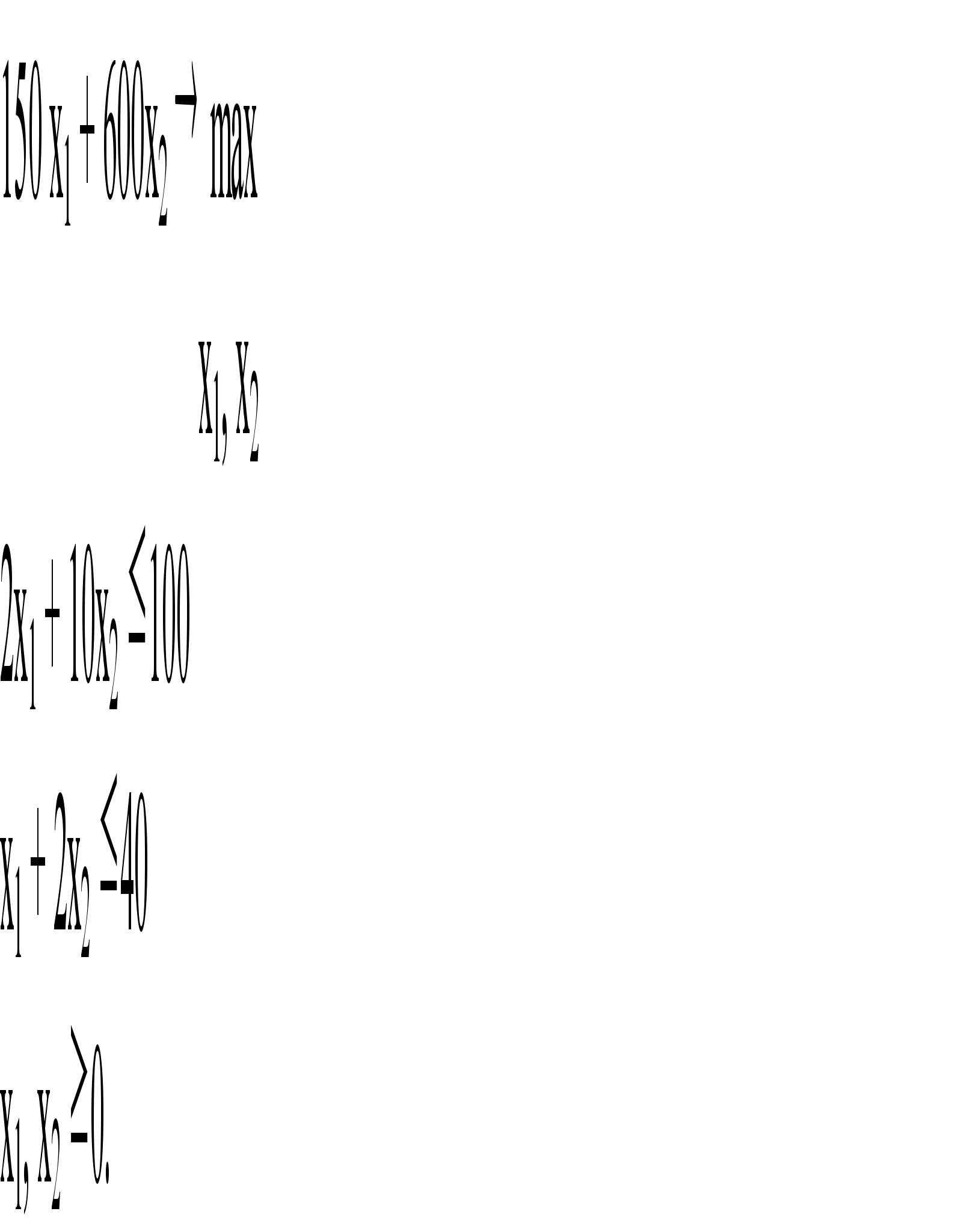
0 комментариев