Навигация
Записать математическую модель задачи
1. Записать математическую модель задачи
| Сырье | Продукция | Общее количество сырья | ||
| А | В | С | ||
| S1 | 15 | 12 | 15 | 360 |
| S2 | 6 | 8 | 4 | 192 |
| S3 | 3 | 2 | 5 | 180 |
| Цена одного изделия (руб.) | 9 | 10 | 16 | |
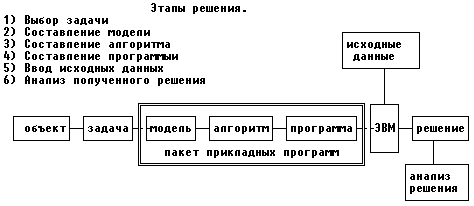
2. Привести задачу к каноническому виду, для этого перейти от ограничений-неравенств к ограничениям-равенствам, для чего вводятся дополнительные переменные, которые по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида.
3. Заполнить симплекс-таблицу.
4. Выяснить, имеется ли хотя бы одно отрицательное число Dj (в строке F, см. таблицу ниже). Если нет, то найденный опорный план оптимален. Если же среди чисел Dj есть отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.
5. Находят направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом Dj, а направляющая строка – минимальным из отношений компонент столбца вектора Р0 к положительным компонентам направляющего столбца.
6. Определяют положительные компоненты нового опорного плана, коэффициенты разложения векторов Pj по векторам нового базиса и числа F0’, Dj’. Все эти числа записываются в новой таблице.
7. Проверяют найденный опорный план на оптимальность. Если план не оптимален и необходимо перейти к новому опорному плану, то возвращаются к пункту 5, а в случае получения оптимального плана или установления неразрешимости процесс решения задачи заканчивается.
Запишем систему ограничений задачи.
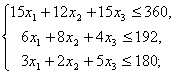
![]() .
.
![]() - целевая функция.
- целевая функция.
Для использования симплекс-метода запишем задачу в следующем виде:
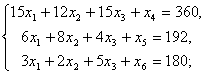
![]() - целевая функция.
- целевая функция.
|
|
|
|
|
|
| b | Отношения | |
|
| 15 | 12 | 15 | 1 | 0 | 0 | 360 |
|
|
| 6 | 8 | 4 | 0 | 1 | 0 | 192 |
|
|
| 3 | 2 | 5 | 0 | 0 | 1 | 180 |
|
| F | -9 | -10 | -16 | 0 | 0 | 0 | 0 | |
|
| 1 | 4/5 | 1 | 1/15 | 0 | 0 | 24 | |
|
| 2 | 24/5 | 0 | -4/15 | 1 | 0 | 96 | |
|
| -2 | -2 | 0 | -1/3 | 0 | 1 | 60 | |
| F | 7 | 14/5 | 0 | 16/15 | 0 | 0 | -384 |
Так как в строке F нет отрицательных элементов (кроме последнего значения), то получен оптимальный план (0;0;24;0;96;60) и максимальное значение целевой функции Fmax=384. Значит, план выпуска продукции составляет 24 изделия вида С.
При данном выпуске продукции полностью используется сырье S3, остаются неиспользованными сырье вида S1,2. Стоимость производимой продукции равна 384 руб.
Задание 3. Транспортная задача
На оптовых складах А1, А2, А3 имеются запасы некоторого продукта в количествах 30, 60 и 10 т соответственно. Найти такой вариант прикрепления магазинов к складам, при котором сумма затрат на перевозку была бы минимальной.
| Склады вооружения | Потребители | Запасы | |||
| N1 | N2 | N3 | N4 | ||
| А1 | 4 | 10 | 11 | 7 | 30 |
| А2 | 5 | 3 | 6 | 8 | 60 |
| А3 | 2 | 1 | 12 | 9 | 10 |
| Потребности | 40 | 20 | 10 | 30 | 100 |
Данная задача является закрытой транспортной задачей, так как суммы потребностей и запасов равны 100.
Решение.
Найдем опорный план методом наименьшей стоимости
| Склады вооружения | Потребители | Запасы | |||
| N1 | N2 | N3 | N4 | ||
| А1 | 4 30 | 10 | 11 | 7 | 30 α1 |
| А2 | 5 10 | 3 10 | 6 10 | 8 30 | 60 α2 |
| А3 | 2 | 1 10 | 12 | 9 | 10 α3 |
| Потребности | 40 β1 | 20 β2 | 10 β3 | 30 β4 | 100 |
Сумма затрат равна F=120+50+30+10+60+240=510.
Правильность опорного решения N=m+n-1=3+4-1=6, это число равно количеству заполненных клеток.
Проверим построенный план на оптимальность методом потенциалов.
Для занятых ячеек:
α1+ β1=4,
α2+ β1=5,
α2+ β2=3,
α2+ β3=6,
α2+ β4=8,
α3+ β2=1.
Пусть α1=0, тогда получаем:
α2=1,
α3=-1,
β1=4,
β2=2,
β3=5,
β4=7.
Для свободных клеток:
D12=с12-(α1+β2)=10-(0+2)=8>0,
D13=с13-(α1+β3)=11-(0+5)=6>0,
D14=с14-(α1+β4)=7-(0+7)=0≥0,
D31=с31-(α3+β1)=2-(-1+4)=-1<0,
D33=с33-(α3+β3)=12-(-1+5)=6>0,
D34=с34-(α3+ β4)=9-(-1+7)=3>0.
Здесь имеются отрицательные значения, в частности, для клетки с тарифом c31. Следовательно, построенный план нуждается в оптимизации, для чего построим цикл пересчета.
| Склады вооружения | Потребители | Запасы | |||
| N1 | N2 | N3 | N4 | ||
| А1 | 4 30 | 10 | 11 | 7 | 30 α1 |
| А2 |
|
| 6 10 | 8 30 | 60 α2 |
| А3 |
| 1 10 - | 12 | 9 | 10 α3 |
| Потребности | 40 β1 | 20 β2 | 10 β3 | 30 β4 | 100 |
Используя цикл пересчета получаем новый опорный план. Проверим правильность опорного решения N=m+n-1=3+4-1=6<5, это число меньше количества заполненных клеток (5 клеток).
| Склады вооружения | Потребители | Запасы | |||
| N1 | N2 | N3 | N4 | ||
| А1 | 4 30 | 10 | 11 | 7 | 30 α1 |
| А2 | 5 | 3 20 | 6 10 | 8 30 | 60 α2 |
| А3 | 2 10 | 1 | 12 | 9 | 10 α3 |
| Потребности | 40 β1 | 20 β2 | 10 β3 | 30 β4 | 100 |
Таким образом, мы получили план, матрица которого является вырожденной, то есть ее определитель равен нулю.
Задание 4. Системы массового обслуживания
Контроль готовой продукции фирмы осуществляют А контролеров. Если изделие поступает на контроль, когда все контролеры заняты проверкой готовых изделий, то оно остается не проверенным. Среднее число изделий, выпускаемых фирмой, составляют В изд./час. Среднее время на проверку одного изделия – С мин.
Определить:
· вероятность того, что изделие пройдет проверку;
· насколько загружены контролеры;
· сколько контролеров необходимо поставить, чтобы Робс.≥D.
Решение.
A=5, B=24, C=6, D=0,98, n=5.
Похожие работы
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...
... + 6y ≤ b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Дать определение умножения матрицы на число. 2) Записать общую задачу ...
... ряд соображений, которые этим расчетом не были учтены. В зависимости от того, какой информацией обладают руководитель и его сотрудники, подготавливающие решения, меняются и условия принятия решений и математические методы, применяемые для выработки рекомендаций. Если известны все действующие в системе факторы, то есть отстствуют случайные воздействия, то это будет принятие решений в ...
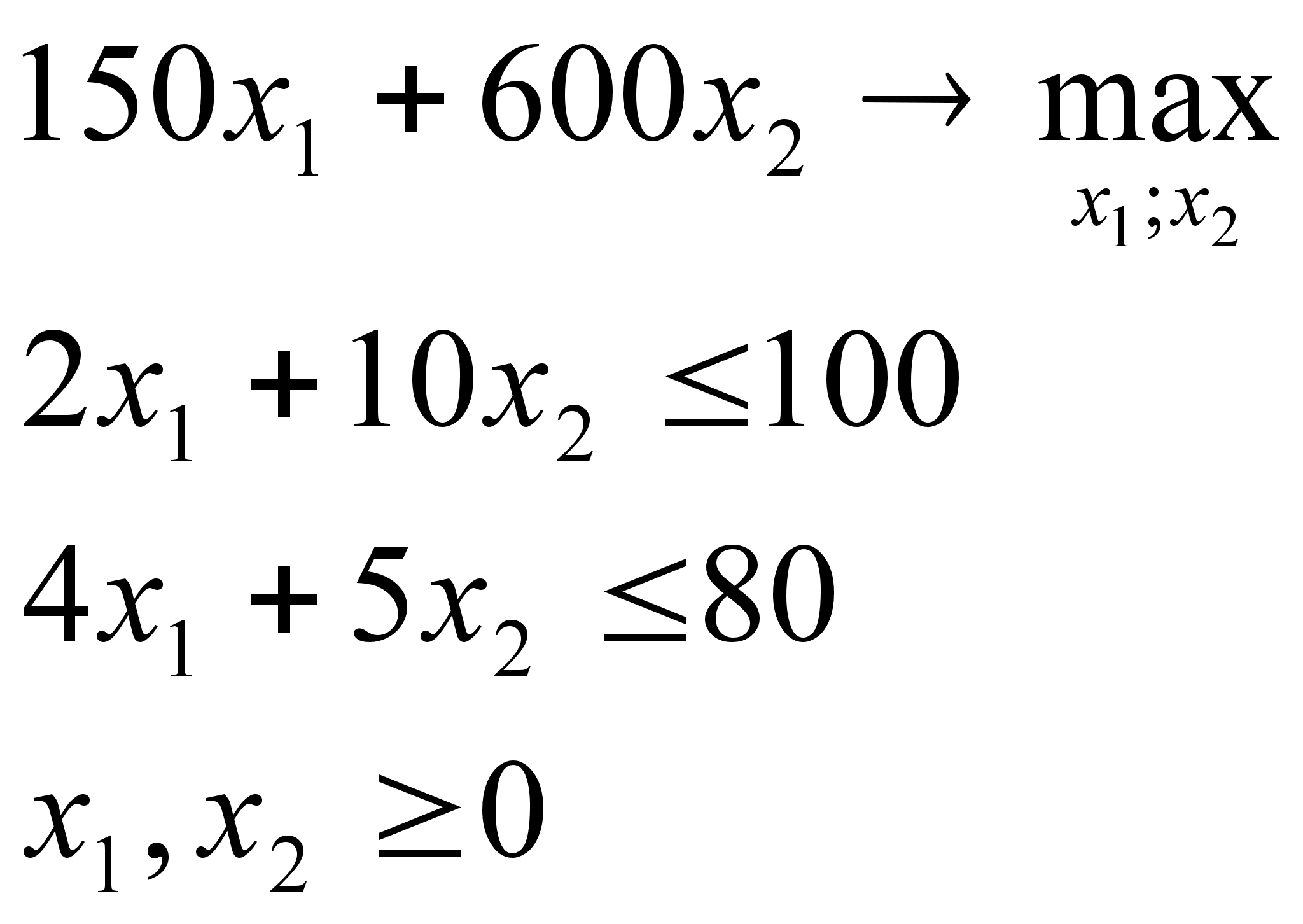
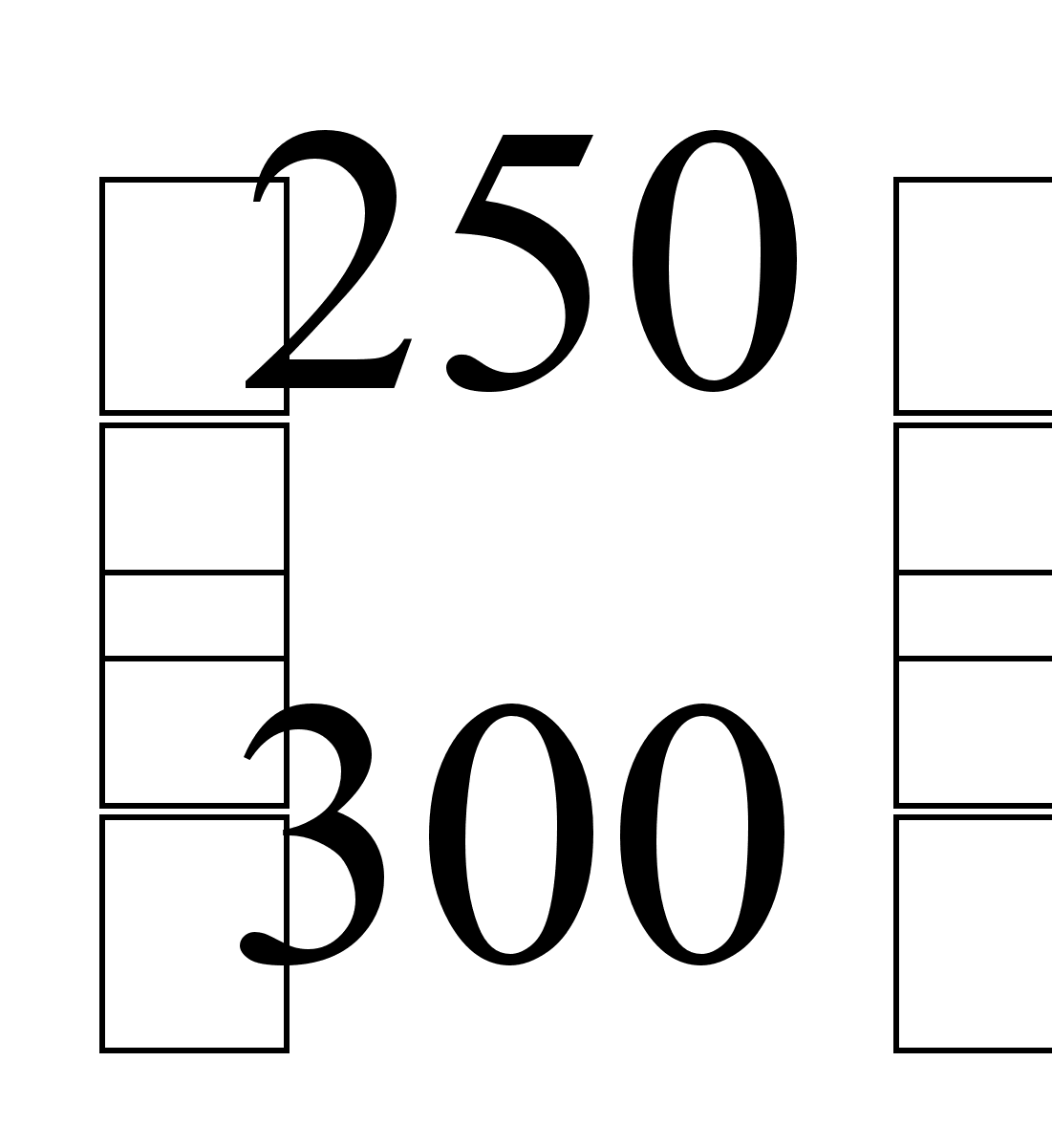
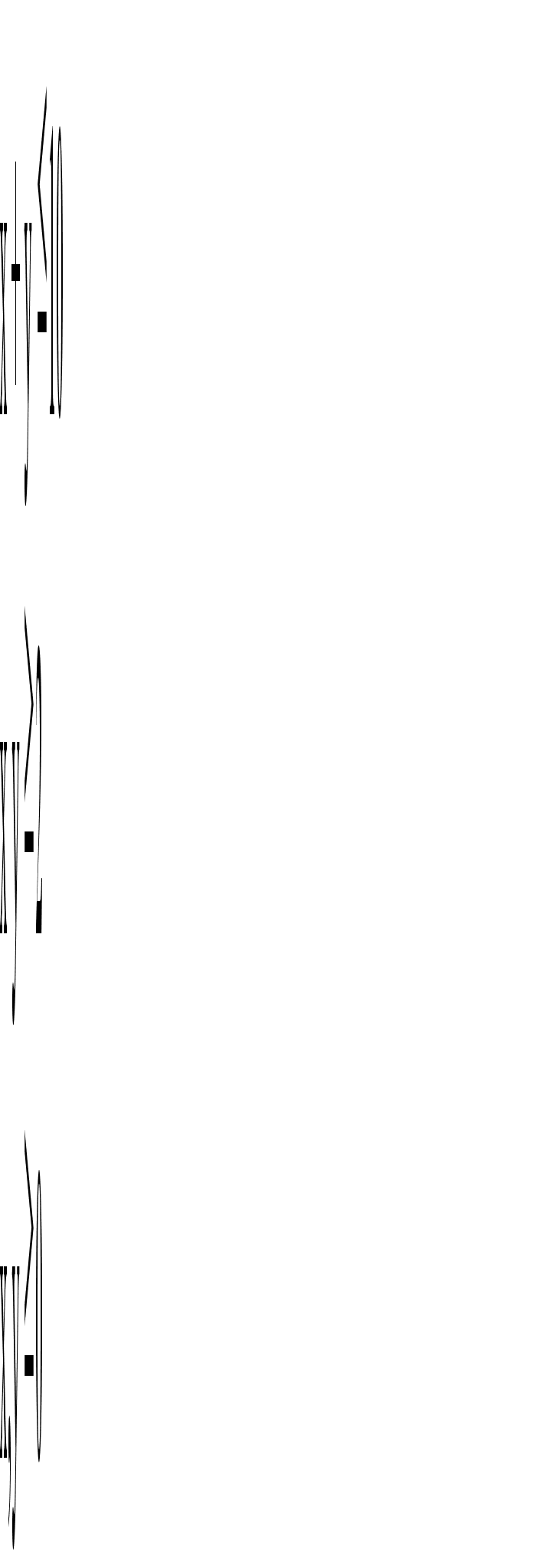
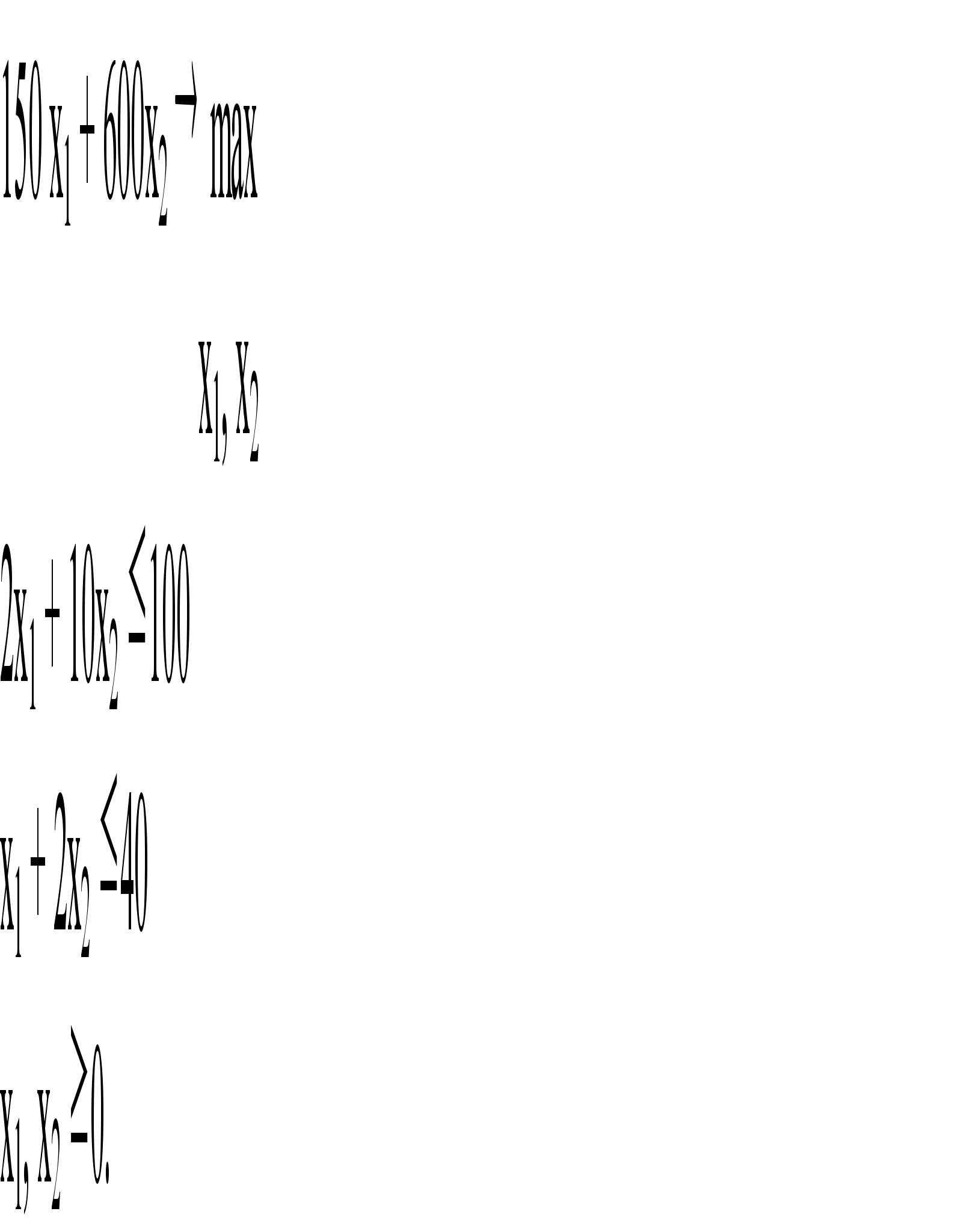
0 комментариев