Навигация
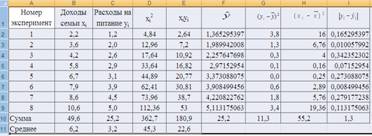
Хср= 49.6/8 = 6.2; Уср= 25.2/8 = 3.2 XcpУср=180,9/8 = 22,6
3. Хср= 49.6/8 = 6.2; Уср= 25.2/8 = 3.2 XcpУср=180,9/8 = 22,6.
Для вычисления среднеквадратических ошибок Sy, Sx имеем формулу:
Sy=√∑(yi-y^i)/n Sx=√∑(xi-x^)^2/n
![]()

Коэффициент корреляции вычислим по формуле:
rxy=xy^-x^*y^/sy*sx
![]()
![]()
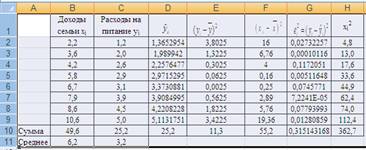
3. Рассчитаем коэффициент детерминации: R2xy = 0,972111224. Значит, 97,2% величины расходов семьи на питание зависит от изменения доходов семьи, а остальные 2,8% связаны с изменением других, не включенных в модель факторов.
![]()
![]()
Вычислим коэффициент эластичности:
Эху=aix^/y^
![]()
![]()
С увеличением доходов семьи на 1% расходы на питание увеличатся в среднем на 0,8781%.
3. Найдем среднюю по модулю линейную относительную ошибку аппроксимации по формуле: d=1/n*∑(yi-y^)
![]()
![]()
Коэффициент низкий что значит точность построения модели высока.
ЗАДАНИЕ №7.
1. По исходным данным из задачи 6 рассчитаем Se, Sa0, Sa1 по формулам. Для этого подготовим таблицу:

Se = √1/n-2*∑e^2
Sa0=Se*√ ∑x ^2/∑(xi-x^)^2
Sa1 = Se*√ 1/∑(x-x^)^2
Согласно задаче имеем:
А0 = 0,3837079А1 = 0,4461762. для вычисления фактических значений t-критерия воспользуемся формулами: ta0 = a0/ Sa0 = 1.84707; ta1 = 14,4617.
По таблице 1 приложения А найдем табличное значение t-критерия для степеней свободы df = 8-1-1 = 6 и уровня зависимости 6%,т.е. tтабл = 1,943.
При уровне значимости 6% имеет место неравенство:
ta1 = 0,073525 ‹ tтабл = 1,943. Значит, с уверенностью 94% можно утверждать, что оценка А1 = 0,747263097 не является статистически значимой.
Аналогично проверим для другого параметра. ta0 = 1,743736 ‹ tтабл = 1,943, значит оценка А0 = 0,123251901 также не является статистически значимой.
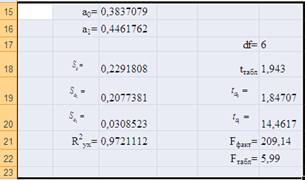

2. Значимость уравнения регрессии в целом и коэффициента тесноты связи R2 определяется с помощью критерия Фишера. Значение оценки R2 получено в предыдущей задаче, R2 = 0,968583448. Фактическое значение Fфакт определяем по формуле: Fфакт = 184,9821.
Табличное значение Fтабл определяем по таблице: Fтабл = 5,99.
Поскольку Fфакт = 184,9821› Fтабл = 5,99, то с уверенностью 94% делается заключение о том, что уравнение регрессии в целом статистически значимо и статистически значим показатель степени связи R2, т.е. отвергается нулевая гипотеза о том, что R2 = 0.
ЗАДАНИЕ №8.
Имеются следующие исходные данные:
| Годы | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Объем реализации | 10,84 | 11,12 | 10,6 | 11,31 | 11,62 | 12,0 | 12,73 | 11,12 |
Коэффициент достоверности аппроксимации для каждого типа линии тренда
1) Линейная у= 0,1795х – 347,71 R^2=0.4163
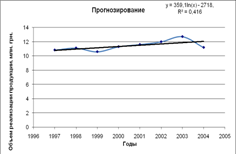
2) Логорифмическая у=359,19 Ln(x)-2718,8 R^2=0.1464
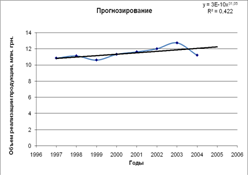
3) Степенная y=3E-102x^31.059 R^2=0.422
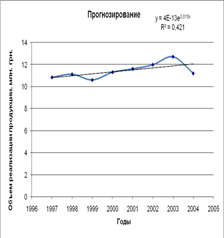
4) Экспонтенциальная у=4Е-13е^0.01558x R^2=0.4218
Как видно из рисунка в 2005г в сравнении с 2004г в среднем реализация продукции увеличилась на 0,42 млн. грн.
ЗАДАНИЕ №9.
Имеются данные испытаний нескольких величин по результатам обследования десяти статистически однородных филиалов фирмы, приведенные в таблице. х1- фондовооруженность, х2 – энерговооруженность, у – производительность труда.
Выполнить следующее:
1. Построить линейную регрессионную модель при помощи ПЭВМ.
2. Выполнить команду «Регрессия».
3. Определить по результатам команды «Регрессия» значение коэффициента множественной корреляции и детерминации.
4. Проверить статистическую значимость оценок параметров модели.
5. Проверить статистическую значимость оценки степени достоверности взаимосвязи R2 и всей модели в целом.
РЕШЕНИЕ.
1. построить регрессионную модель.
2. выполнить команду «Регрессия», результаты которой показаны ниже.
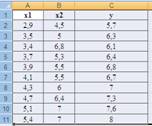
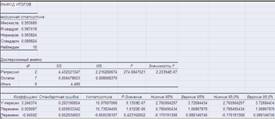
Рис. Результаты команда «Регрессия»
Регрессионная модель принимает вид:
у^ = 0929087*2,9+ - 0,4502*4,5-3,246374
3. Согласно Рис коэффициенты множественной корреляции и детерминации,в данном случае R = 0,993689; R2 = 0,98742.
4. Статистическую значимость оценок параметров модели b,a1,а2 осуществим с помощью t-критерия. Для этого определим его табличное значение и его фактические значения для каждого из оцениваемых параметров. По таблице 1 приложения А при уровне значимости 1% найдем табличное значение t-критерия для степеней свободы df = 10-2-1 = 7 и уровня зависимости 7%,т.е. tтабл = 3,143.
Фактическое значение t-критерия для каждого из оцениваемых параметров смотрим на рисунке в столбце t-статистика в нашем случае:
t-a1= 15,73834 ta2= - 0,855361 tb=15,97697
При уровне значимости 7% t-a1= 15,73834> tтабл имеет место равенство: Значит, с уверенностью 99% можно утверждать, что оценка А1 параметра модели является статистически значимой.
Условие ta2 = -0,855361< tтабл = 3,143 не выполняется, значит утверждаем, что этот критерий статистически не важен.
Условие tв = 15.97697> tтабл = 3,143 выполняется, значит и эта оценка статистически значима в модели.
5. Значимость уравнения регрессии в целом и коэффициента тесноты связи R2 определяем с помощью критерия Фишера. Фактическое Fфакт =274,684752
Табличное значение Fтабл определяем по таблице: Fтабл = 9,55. Условие Fфакт =274684752> Fтабл = 9.55 выполняется, поэтому с вероятностью 99% делается заключение о том, что R2 статистически значим, и уравнение регрессии в целом значимо, т.е. отвергается нулевая гипотеза R2 = 0.
Похожие работы
... к составлению математических моделей. Если математическая модель - это диагноз заболевания, то алгоритм - это метод лечения. Можно выделить следующие основные этапы операционного исследования: наблюдение явления и сбор исходных данных; постановка задачи; построение математической модели; расчет модели; тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют ...
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...
... часто представляются в виде алгоритма, в котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи. Обычно модель возникает как необходимый этап решения конкретной задачи. Однако в дельнейшем может происходить обособление модели от задачи, и модель начинает жить самостоятельно. Примером может служить сюжет ...
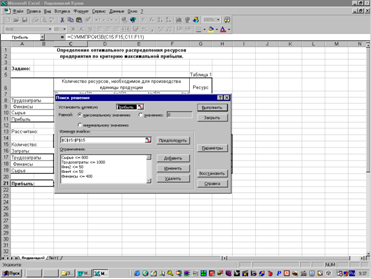
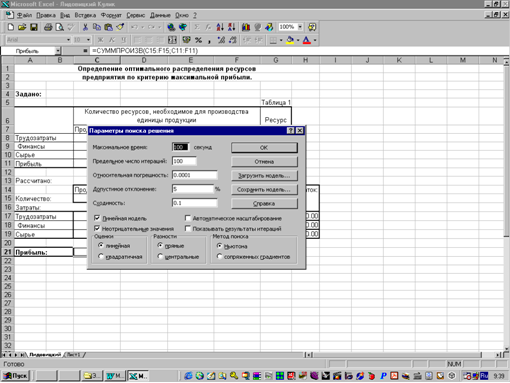
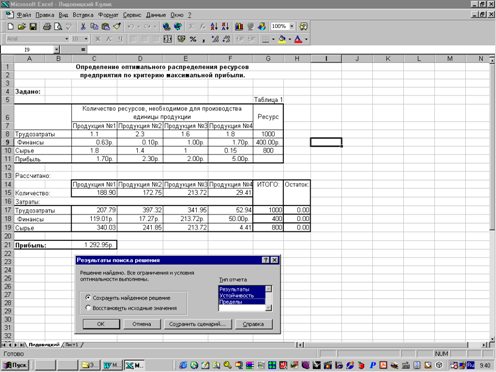
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...

0 комментариев