Задание 1. Найти производные функций
a) ![]()
Пусть ![]() ,
, ![]() , тогда
, тогда ![]()
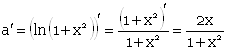

![]()
b) ![]()
Если функция имеет вид ![]() , то её производная находится по формуле
, то её производная находится по формуле ![]() .
.
Перейдем от десятичного логарифма к натуральному: ![]()
По свойству логарифма ![]()
Таким образом,

c) ![]()
Продифференцируем уравнение, считая y функцией от х:
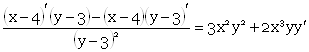
![]()
![]()
![]()
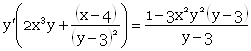
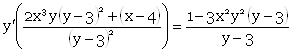
![]()
![]()
Задание 2. Исследовать методами дифференциального исчисления и построить график функции ![]()
Областью определения функции являются все действительные числа,
кроме х=0. В точке х=0 функция разрывна.
Функция нечетная, т. к. ![]()
Функция не пересекается с осями координат (уравнение y=0 не имеет решений).
Найдем производную функции:
![]() .
.
![]() Найдем стационарные точки, приравняв производную к нулю.
Найдем стационарные точки, приравняв производную к нулю.
 | ||||||||
Функция возрастает в промежутке (-∞; – 1) U (1; ∞)
и убывает в промежутке (-1; 0) U (0; 1).
Функция имеет экстремумы: максимум – в точке х=-1, минимум – в точке х=1.
Исследуем функцию на выпуклость / вогнутость.
Для этого найдем производную второго порядка и, приравняв её к нулю, вычислим критические точки второго рода.

![]()

В точке х=0 вторая производная не существует, т. к. это точка разрыва функции. В интервале (-∞; 0) ![]() <0, следовательно, график функции в этом интервале выпуклый. В интервале (0;∞)
<0, следовательно, график функции в этом интервале выпуклый. В интервале (0;∞) ![]() >0, следовательно, график функции в этом интервале вогнутый.
>0, следовательно, график функции в этом интервале вогнутый.
Асимптоты графика функции ![]() :
:
1) вертикальная асимптота – прямая х=0
Т.к. ![]() и
и ![]()
2) горизонтальных асимптот нет,
т. к. ![]() и
и ![]()
3) наклонных асимптот нет,
т. к. 
и 
Задание 3. Найти экстремумы функции Z = ln (3 – x2 + 2x – y2)
Найдем частные производные первого порядка.
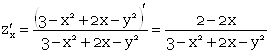
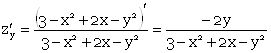
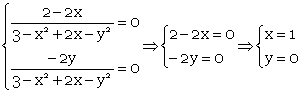
М (1; 0) – стационарная точка.
Найдем вторые производные и их значения в точке М.


![]()
![]() >0
>0 ![]() Следовательно, функция Z = ln (3 – x2 + 2x – y2) имеет экстремум в точке М (1; 0) – максимум, т. к. A< 0.
Следовательно, функция Z = ln (3 – x2 + 2x – y2) имеет экстремум в точке М (1; 0) – максимум, т. к. A< 0.
Задание 4. Вычислить неопределенные интегралы, результат проверить дифференцированием
a) ![]()
Решаем методом замены переменной. Положим ![]() ,
,
тогда ![]()
![]()
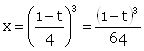 ,
,
![]()
![]()
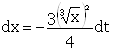
Таким образом, получаем
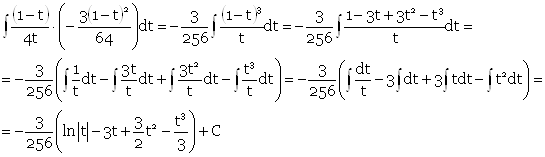
Вернемся к переменной х.
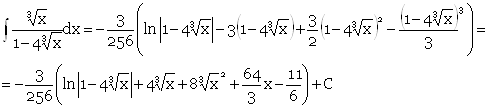
Проверим дифференцированием:

b) ![]()
Воспользуемся таблицей неопределенных интегралов [Выгодский, М.Я. Справочник по высшей математике. – М.: Наука, 1972. – 872 с.:ил. – С. 850]
![]() С
С
Проверим дифференцированием:

c)![]()
Неправильную рациональную дробь приводим к правильной делением числителя на знаменатель, получаем
![]()
Согласно свойству интервала алгебраической суммы, имеем
![]()
![]()
![]()
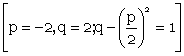
Подстановка ![]()
![]()
![]()
![]()
![]() приводит интеграл к виду
приводит интеграл к виду
![]()
Возвращаясь к аргументу х, получаем
![]()
Таким образом, ![]() ,
,
где С=С1+С2
Проверим дифференцированием:
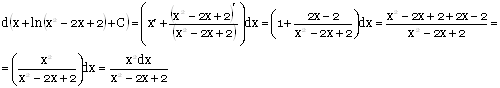
Задание 5. Вычислить определенный интеграл

Сначала вычислим неопределенный интеграл методом замены переменной. Полагая ![]() , находим
, находим
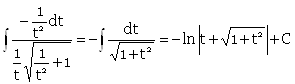
Вернемся к переменной х.
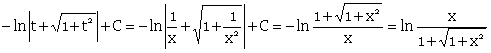
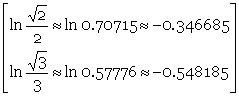 Таким образом,
Таким образом, 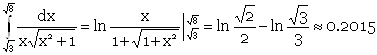
Библиографический список
1. Баврин, И.И. Высшая математика: учебник/ И.И. Баврин. – М.: Академия, 2003. – 616 с.:ил.
2. Выгодский, М.Я. Справочник по высшей математике/М.Я. Выгодский. – М.: Наука, 1972. – 872 с.:ил.
3. Выгодский, М.Я. Справочник по элементарной математике/М.Я. Выгодский. – СПб.: Изд. «Санкт-Петербург оркестр», 1994. – 416 с.:ил.
Похожие работы
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
... же этих неизменных вещей следует вести в онтологических регионах, максимально далеких от региона вещей: в области эйдосов, в области чистого сознания, логики и т.п. Вполне возможно, "матаналитическая" теория познания к эйдетическому типу познания не применима. Однако может быть, применима. Это вопрос открытый. Следующее понятие, которое необходимо ввести в теорию Лосева: интуитивное знание. Я ...
... зависимость от параметра. Рассматривая интеграл Коши, мы видим, что подынтегральная функция зависит от двух комплексных переменных: переменной интегрирования и фиксированного значения переменной . Тем самым интеграл Коши является интегралом, зависящим от параметра. Естественно поставить вопрос об общих свойствах интегралов по комплексной переменной, зависящих от параметра. Пусть задана функция ...
... развития должны иметь право выбрать свой путь: принимать участие в жизни общества, либо предпочесть защищенность и уединение. 1.5 Коррекционная направленность воспитания и обучения детей с задержкой психического развития Вся деятельность специального дошкольного учреждения базируется на соблюдении основополагающих принципов и подходов к вопросам изучения, воспитания и обучения детей ...

0 комментариев