Конспект урока по математие для учащихся 6 "Б" класса
Тема урока: Длина окружности и площадь круга
Цели: ввести формулу площади круга и научить применять ее к решению задач; закрепить полученные знания в ходе выполнения упражнений, развивать логическое мышление учащихся.
Тип урока: изучение нового материала.
Оборудование: плакаты с формулами длины окружности и площади круга.
I. Устная работа (актуализация знаний)
1. Решить № 858 (а; б; в) устно и № 859 (в; г).
№ 858 (а; б; в)
![]()
№ 859 (в; г).
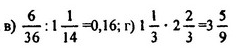
2. Решить задачу, повторив формулу длины окружности с = pd: определите диаметры стволов деревьев-гигантов у их оснований: а) эвкалипта, длина окружности которого 25 м; б) мамонтова дерева, длина окружности которого 32 м.
II. Объяснение нового материала
1. Кругом называется часть плоскости, ограниченная окружностью. Например, дно стакана, поверхность крышки консервной банки.
2. Работа по рисунку 40 учебника на с. 138.
Если площадь круга обозначить через S, то ее можно вычислить по формуле ![]() .
.
3. Вычислить площадь круга, радиус которого равен 5 см.
Решение.
S = pr2 = 3,14 · 52 = 3,14 · 25 = 78,5 (см2).
Ответ: 78,5 см2.
4. (Устно.) Вычислить площадь круга, диаметр которого равен 2 см; 20 см; 0,2 см.
5. Начертите круг. Измерьте его радиус и вычислите площадь круга.
III. Тренировочные упражнения
1. Решить задачу № 854 на доске и в тетрадях.
Решение.
с = 40,8 м;![]()
Диаметр арены цирка 13 м, радиус 6,5 м. Площадь арены цирка равна
S = pr2 = 3 · 6,52 » 3 42,25 » 126,75 (м2) » 127 м2.
Ответ: 13 м; »127 м2.
2. Решить задачу № 855 на доске и в тетрадях.

3. Решить задачу № 853 самостоятельно, используя рисунок 42 учебника и выполнив измерения радиуса каждой окружности.
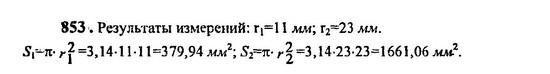
4. Решить задачу (объясняет учитель):
Останкинская телебашня в Москве опирается на площадку, имеющую форму кольца. Диаметр наружной окружности 63 м, а внутренней окружности 44 м. Вычислите площадь фундамента Останкинской телебашни.
Решение.
Sкольца = pr12 – pr22 = p(r12 – r22); p » 3.
r1= 63 : 2 = 31,5 (м); · r2= 44 : 2 = 22 (м);
Sкольца = 3 · (31,52 – 222) = 3 (992,25 – 484) = 3 · 508,25 =
= 1524,75 (м)2 » 1525 м2.
Ответ: 1525 м2.
IV. Итог урока
1. Повторить все формулы по теме.
2. Что называется кругом?
3. Как разделить круг на две равные части?
4. Найдите площадь ![]() круга, радиус которого 4,4 дм. Число p округлите до десятых.
круга, радиус которого 4,4 дм. Число p округлите до десятых.
Домашнее задание: запомнить формулы п. 24; решить № 856, 870, 871.
Литература
1. Математика. 6 класс. Виленкин Н.Я., Жохов В.И. и др. 13-е и 23 изд., перераб. - М: Мнемозина, 2004 и 2008 гг.
2. Математика. 6 класс: поурочные планы (по учебнику Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда). I полугодие. 3-е изд., перераб. и исправлен. / авт.-сост. Л. А. Тапилина. Т. Л. Афанасьева. – Волгоград: Учитель, 2008. – 173 с.
3. Математика. 6 класс: поурочные планы (по учебнику Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда). II полугодие. 3-е изд., перераб. и исправлен. / авт.-сост. Л. А. Тапилина. Т. Л. Афанасьева. – Волгоград: Учитель, 2008. – 143 с.
Похожие работы
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... ) и теория диофантового приближения (раздел теории чисел, в котором изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов). 2.6. Теон и Гипатия Учеными, завершившими цикл математиков Александрийской школы, были Теон (IV в.) и его дочь Гипатия (370—415). Теон проделал большую работу, комментируя труды Евклида и Птолемея. Что же касается Гипатии, то, по отзывам ...
... , вертели ее так и сяк... Как это похоже на современного ребенка, который играет за экраном компьютера, не подозревая о том, на что способна эта машина! 6. Закат греческой математики Во 2 веке до н.э. расцвет греческой науки прекратился. Это было неизбежно: толпу на улицах имперских столиц теперь волновали совсем иные проблемы, чем квадратура круга или движение Марса среди звезд. Математика ...
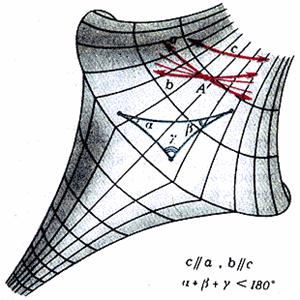
... конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости. Впоследствии, с развитием и введением в математику аксиоматического метода, под Рисунок 4 интерпретацией (или моделью) некоторой системы аксиом стали понимать ...







0 комментариев